【TensorFlow线性回归】：代码实践与深度解读

# 1. TensorFlow线性回归基础

## 1.1 什么是TensorFlow？

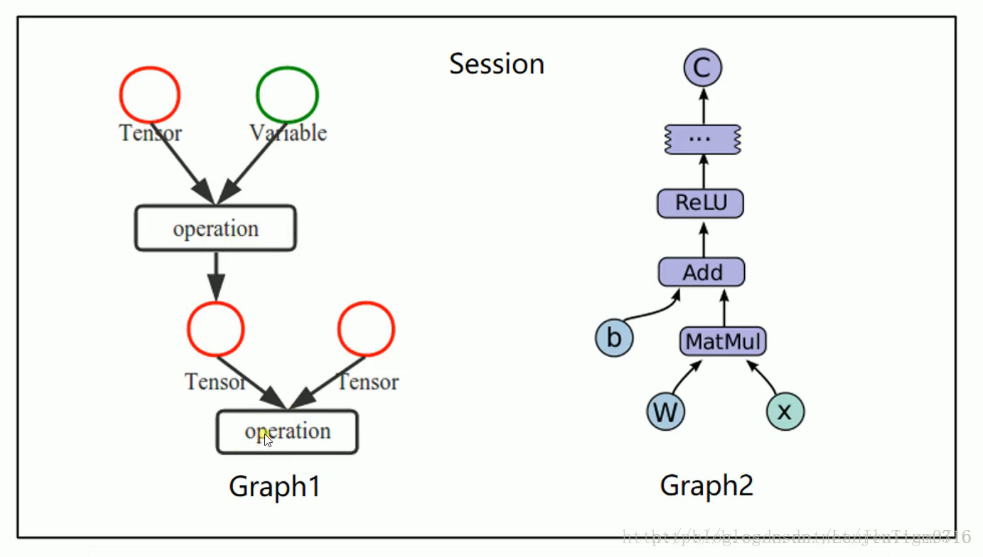
TensorFlow是由Google开发的一个开源机器学习库，广泛应用于数据分析、神经网络建模等领域。它提供了一个灵活的编程框架，能够在多种硬件平台上运行，包括CPU、GPU和TPU。TensorFlow的核心是数据流图，通过将计算任务表示为图，可以有效地进行分布式计算，从而加速机器学习模型的训练。

## 1.2 线性回归简介

线性回归是机器学习中最简单的模型之一，用于预测连续值输出。其基本思想是找到最佳的权重参数，使得通过这些参数的线性组合可以最好地拟合数据。在TensorFlow中实现线性回归可以帮助我们理解如何构建更复杂的机器学习模型。

## 1.3 TensorFlow中的线性回归实现

在TensorFlow中实现线性回归模型的流程一般包括定义计算图、初始化变量、运行会话以及计算损失和优化变量等步骤。通过具体的编程实践，我们可以掌握如何利用TensorFlow构建线性回归模型，并为后续学习更复杂模型打下坚实基础。

# 2. TensorFlow线性回归的理论基础

### 2.1 线性回归的数学原理

#### 2.1.1 线性回归的基本概念

线性回归是统计学中用来预测和解释两个或多个变量间关系的常用方法。其中最简单的是单变量线性回归，它试图通过一个独立变量x来预测因变量y。线性回归假设变量之间存在线性关系，即目标变量与预测变量的关系可以通过一条直线来表示。数学上，这种线性关系可以表示为:

y = ax + b + ε

其中，y是目标变量，x是预测变量，a是斜率，b是截距，ε是误差项，表示无法通过变量x来解释的y的变异部分。

#### 2.1.2 最小二乘法和损失函数

最小二乘法是线性回归中估计模型参数的常用方法。通过最小化误差的平方和来寻找最佳的拟合直线。在数学上，损失函数定义为所有误差平方和，表示为：

L = \sum_{i=1}^{n} (y_i - (ax_i + b))^2

其中，n是样本数量，y_i是第i个样本的目标值，x_i是第i个样本的预测值，L是损失函数值。目标是最小化损失函数，找到最佳的a和b值，使得预测值尽可能接近实际值。

### 2.2 TensorFlow中的线性回归模型

#### 2.2.1 TensorFlow的基本使用方法

TensorFlow是一个开源的机器学习库，用于进行数值计算。其核心是数据流图(data flow graph)，可以用来描述计算过程中的各种操作和变量。创建一个基础的TensorFlow程序通常包括以下步骤:

1. 导入TensorFlow库。
2. 定义模型参数和数据结构。
3. 构建模型结构。
4. 初始化变量。
5. 训练模型。
6. 输出训练结果。

一个基本的TensorFlow程序示例如下：

import tensorflow as tf

# 定义模型参数
a = tf.Variable([0.0], dtype=tf.float32)
b = tf.Variable([0.0], dtype=tf.float32)

# 构建模型结构
def linear_regression(x):
    return a * x + b

# 模型训练过程中的操作
loss_op = tf.reduce_mean(tf.square(y - linear_regression(x)))

# 优化器选择和训练步骤
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(loss_op)

# 初始化变量
init = tf.global_variables_initializer()

# 会话运行，执行模型训练
with tf.Session() as sess:
    sess.run(init)
    # 执行优化器进行模型训练...

#### 2.2.2 TensorFlow中的线性回归实现

使用TensorFlow实现线性回归模型的核心在于构建损失函数和优化器。在上述代码示例中，我们定义了一个`linear_regression`函数，它表示了预测的线性关系，并且构建了损失函数`loss_op`。接着我们选择了梯度下降优化器`GradientDescentOptimizer`，并指定了学习率。

在实际应用中，我们还会使用数据集来训练模型。TensorFlow提供了许多内置的数据集，例如MNIST手写数字识别数据集，用于快速实现模型训练。一旦数据集准备就绪，我们便可以利用其`train()`方法来训练模型，并通过迭代不断优化参数a和b的值，直到模型收敛。

TensorFlow还支持自动微分机制，这意味着用户无需手动计算偏导数，只需定义好损失函数，TensorFlow就能自动求解出梯度，极大地方便了模型的实现和优化过程。

以上所述，是对第二章“TensorFlow线性回归的理论基础”部分的深入解读。在下一章中，我们将继续探索TensorFlow线性回归的代码实现，了解如何通过具体的代码示例，将理论应用于实践。

# 3. TensorFlow线性回归的代码实现

在探讨了线性回归的基础理论之后，我们进入了实际编码的环节，这将让我们的学习之旅更加生动和贴近实际应用。本章节将聚焦于TensorFlow框架下的线性回归模型的构建过程，包括数据准备、处理、模型训练、测试与评估等关键步骤。

## 3.1 数据的准备和处理

线性回归模型的构建离不开数据的支持。在机器学习中，数据是构建模型的基石，而数据的准备和处理是构建有效模型的重要前提。

### 3.1.1 数据的加载和预处理

在实际应用中，数据常常以非结构化的形式存在，如文本、图片等，而模型需要的是结构化的数值数据。因此，数据的加载和预处理是至关重要的一步。

import tensorflow as tf
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split

# 使用sklearn内置的波士顿房价数据集
boston = datasets.load_boston()
X, y = boston.data, boston.target

# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 将数据转换为tensorflow中的常量类型
X_train = tf.constant(X_train, dtype=tf.float32)
X_test = tf.constant(X_test, dtype=tf.float32)
y_train = tf.constant(y_train, dtype=tf.float32)
y_test = tf.constant(y_test, dtype=tf.float32)

在上述代码中，我们首先使用sklearn库中的内置数据集进行演示。在加载数据集后，我们通过`train_test_split`方法将数据分为训练集和测试集，以便于后续的模型评估。然后，我们将NumPy数组转换为TensorFlow常量，以便于后续操作。

### 3.1.2 特征工程和数据标准化

特征工程是指从原始数据中选择、构造和转换特征的过程，这是机器学习项目中的关键步骤。数据标准化是特征工程中常见的处理方式，它可以消除不同量纲导致的影响，使模型训练更为稳定。

from sklearn.preprocessing import StandardScaler

# 对数据进行标准化处理
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 将标准化后的数据转换为tensorflow常量
X_train_scaled = tf.constant(X_train_scaled, dtype=tf.float32)
X_test_scaled = tf.constant(X_test_scaled, dtype=tf.float32)

在这段代码中，我们使用了`StandardScaler`对数据进行标准化处理，并将结果转换为TensorFlow常量。数据的标准化处理有助于加快模型的收敛速度，并提高模型的性能。

## 3.2 线性回归模型的训练和测试

在数据准备完毕后，接下来的步骤是模型的搭建和训练。这一过程涉及到模型的定义、参数的初始化、训练过程的实施、模型的评估等多个环节。

### 3.2.1 模型的搭建和训练

在TensorFlow中，模型可以使用`tf.keras`模块中的`Sequential`模型或者使用函数式API来搭建。本例中，我们使用`Sequential`模型来构建一个简单的线性回归模型。

# 定义线性回归模型
model = tf.keras.Sequential([
    tf.keras.layers.Dense(units=1, input_shape=(X_train_scaled.shape[1],))
])

# 编译模型
***pile(optimizer='sgd', loss='mse')

# 模型训练
model.fit(X_train_scaled, y_train, epochs=100, verbose=1)

在上述代码中，我们首先定义了一个Sequential