【过拟合防御术】：TensorFlow中的正则化技术实施指南

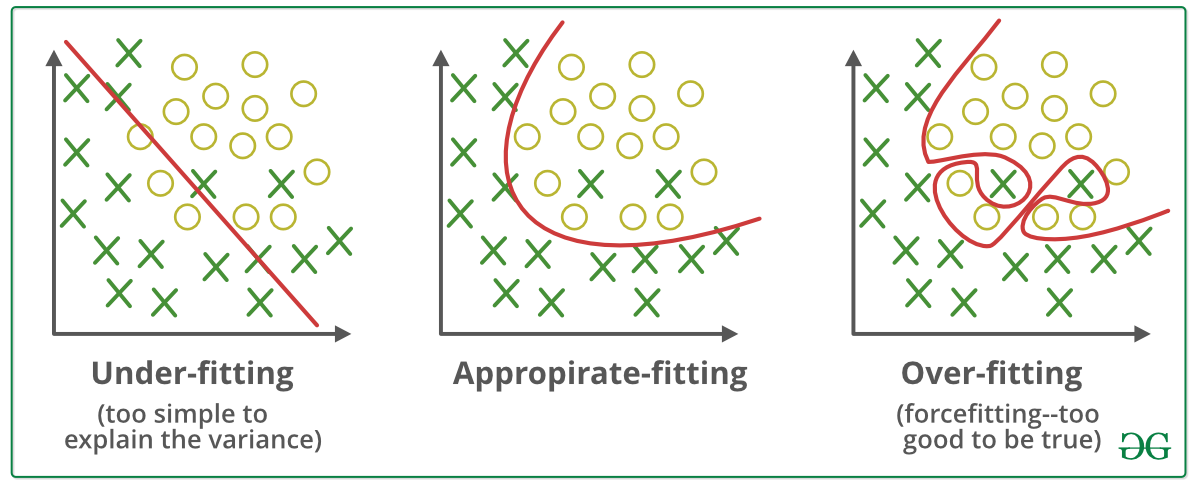
# 1. 过拟合现象及其影响

在机器学习中，尤其是深度学习领域，过拟合是影响模型泛化能力的主要问题之一。**过拟合现象**发生于模型在训练数据上学习得过于“细致”，捕捉到了数据中的随机噪声和异常值，而忽视了数据的真实分布规律。结果是，虽然模型在训练集上的表现极佳，但在未知的新数据上的表现却大打折扣。

过拟合的**影响**是深远的。首先，它导致模型的泛化能力弱，无法有效地推广到实际应用中。其次，过拟合会增加模型的复杂度，使得模型难以理解和维护。最后，模型在实际应用中的表现不佳，不仅降低了用户对模型的信任度，也可能影响到整个项目的成功。

为了避免过拟合，研究者们提出了许多**技术手段**，如数据增强、早停法、Dropout以及正则化技术等。其中，正则化技术是通过给模型的损失函数添加一个额外的惩罚项来控制模型复杂度，提高模型的泛化能力。本书后续章节将深入探讨正则化技术的理论与实践应用，帮助读者更好地理解和运用这一重要技术。

# 2. 理解正则化技术

正则化技术是防止机器学习模型过拟合的重要方法。在深度学习中，这一技术尤为重要，因为模型结构越复杂，就越容易发生过拟合现象。理解正则化技术，可以帮助我们更好地设计和训练模型。

## 2.1 正则化的基本概念

### 2.1.1 过拟合与正则化的关系

在机器学习中，过拟合是指模型在训练数据上表现良好，但在新数据上表现较差的现象。过拟合的模型捕捉了训练数据中的噪声和异常值，失去了泛化能力。

正则化技术是解决过拟合问题的有效手段。正则化通过向损失函数添加一个额外的惩罚项，限制了模型复杂度，从而使得模型能够在训练集和测试集上都保持良好的性能。

### 2.1.2 正则化的理论基础

正则化在数学上通常表达为在损失函数中添加一个惩罚项，使得模型在追求最小化训练误差的同时，也能控制模型参数的大小。这种方法基于一个基本假设，即简单的模型更有可能拥有更好的泛化能力。

## 2.2 正则化的方法论

### 2.2.1 L1正则化（Lasso回归）

L1正则化，又称Lasso回归，是在损失函数中添加绝对值惩罚项。这种正则化倾向于产生稀疏的权重矩阵，即将一些权重压缩至零，因此它对于特征选择特别有效。

公式表示为：
\[ J(w) = J_{loss}(w) + \lambda \sum_{i=1}^{n} |w_i| \]

其中，\( J_{loss}(w) \) 表示未正则化的损失函数，\( w \) 是模型参数，\( \lambda \) 是正则化强度参数。

代码实现示例（假设使用Python和Scikit-learn库）：

from sklearn.linear_model import Lasso
from sklearn.datasets import make_regression

# 创建一个回归数据集
X, y = make_regression(n_samples=100, n_features=10, noise=0.1)

# 创建并训练Lasso回归模型
lasso = Lasso(alpha=0.1) # alpha 是正则化强度
lasso.fit(X, y)

### 2.2.2 L2正则化（Ridge回归）

L2正则化，又称Ridge回归，在损失函数中添加平方惩罚项。它倾向于使权重值接近于零，但不会像L1正则化那样使它们完全为零。

公式表示为：
\[ J(w) = J_{loss}(w) + \lambda \sum_{i=1}^{n} w_i^2 \]

代码实现示例：

from sklearn.linear_model import Ridge

# 创建并训练Ridge回归模型
ridge = Ridge(alpha=0.1) # alpha 是正则化强度
ridge.fit(X, y)

### 2.2.3 弹性网络（Elastic Net）

弹性网络是结合了L1和L2正则化的正则化方法，它在损失函数中同时添加了绝对值和平方的惩罚项。这样既保留了L1正则化对特征选择的能力，也保留了L2正则化对权重大小的控制。

公式表示为：
\[ J(w) = J_{loss}(w) + \lambda_1 \sum_{i=1}^{n} |w_i| + \lambda_2 \sum_{i=1}^{n} w_i^2 \]

代码实现示例：

from sklearn.linear_model import ElasticNet

# 创建并训练弹性网络模型
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5) # alpha 是正则化强度，l1_ratio 是L1与L2正则化系数的比值
elastic_net.fit(X, y)

## 2.3 正则化在模型中的作用机制

### 2.3.1 权重衰减

正则化的主要作用之一是通过权重衰减来控制模型复杂度。权重衰减意味着模型会偏好较小的权重值。这有助于降低模型对训练数据中的小波动或噪声的敏感性，因此能提高模型的泛化能力。

### 2.3.2 降低模型复杂度

除了权重衰减，正则化还通过直接控制模型的复杂度来防止过拟合。L1和L2正则化通过惩罚项的添加，使得模型在复杂度和训练误差之间达到一种平衡，避免了模型过度适应训练数据。

在实际应用中，选择合适的正则化技术及其参数是非常关键的。模型的性能往往会随着正则化强度的不同而有显著的差异。因此，调整正则化参数以达到最佳效果是模型调优过程中的一个重要环节。

| 正则化技术 | 权重衰减 | 特征选择 | 泛化能力 |
|-----------|--------|---------|---------|
| L1正则化 | 强 | 有 | 一般 |
| L2正则化 | 适中 | 无 | 好 |
| 弹性网络 | 适中 | 有 | 较好 |

通过比较不同正则化技术的特点，我们可以根据具体问题和模型结构来选择合适的正则化方法，从而达到减少过拟合、提升模型泛化能力的目的。

# 3. TensorFlow中的正则化实现

在深度学习模型中，正则化技术是减少过拟合现象的关键手段之一。正则化能够通过向模型的损失函数中添加一个额外的项来限制模型的复杂度，防止模型在训练数据上学习到过于复杂的特征，从而在新的、未知的数据上泛化能力较差。TensorFlow作为一个开源的机器学习库，提供了丰富的工具来实现各种正则化技术。

## 3.1 TensorFlow简介及安装

### 3.1.1 TensorFlow的核心组件

TensorFlow的核心概念是张量（Tensor）和计算图（Graph）。张量类似于多维数组，它们可以是标量、向量、矩阵，也可以是更高维的数据结构。计算图描述了张量之间的运算关系，它由节点（操作）和边（数据流向）组成，每个节点执行特定的运算，边表示数据的流动。TensorFlow的优势在于自动微分和分布式执行能力，这使得其在大规模的机器学习任务中表现出色。

### 3.1.2 安装和配置TensorFlow

安装TensorFlow相对简单，可以通过Python的包管理工具pip进行安装。推荐使用虚拟环境来安装TensorFlow，以避免版本冲突。以下是安装的常用命令：

# 创建并激活虚拟环境
python -m venv myenv
source myenv/bin/activate  # 在Windows下使用 myenv\Scripts\activate

# 安装TensorFlow
pip install tensorflow

为了验证TensorFlow是否安装成功，可以运行以下Python代码：

import tensorflow as tf

print(tf.__version__)

若打印出了版本号，则说明TensorFlow已经安装成功。

## 3.2 TensorFlow中正则化的代码实现

### 3.2.1 使用内置函数添加正则化

TensorFlow提供了内置的正则化函数，它们可以很容易地集成到模型中。对于L1和L2正则化，可以通过`tf.contrib.layers`模块中的`l1_regularizer`和`l2_regularizer`函数来实现。

import tensorflow as tf
from tensorflow.contrib import layers

def build_model():
    # 定义一个简单的模型结构
    inputs = tf.placeholder(tf.float32, shape=[None, 784])
    outputs = layers.fully_connected(inputs, 10, 
                                     regularizers={'l1': 0.01, 'l2': 0.01})
    return inputs, outputs

在这个例子中，我们创建了一个具有10个神经元的全连接层，并为该层的权重添加了L1和L2正则化项，正则化系数分别为0.01。

### 3.2.2 自定义正则化项

在某些情况下，内置的正则化函数可能无法满足特定的需求，这时我们可以自定义正则化项。自定义正则化函数可以被加入到损失函数中，从而实现正则化的效果。

def my_regularization(weights):
    reg = tf.nn.l2_loss(weights)
    return reg

weights = tf.Variable(tf.random_normal([784, 10]), name='weights')
bias = tf.Variable(tf.zeros([10]), name='bias')

regularization_loss = my_regularization(weights)
loss = tf.reduce_mean(tf.square(tf.matmul(in