ReLU激活函数：解决梯度弥散问题的关键

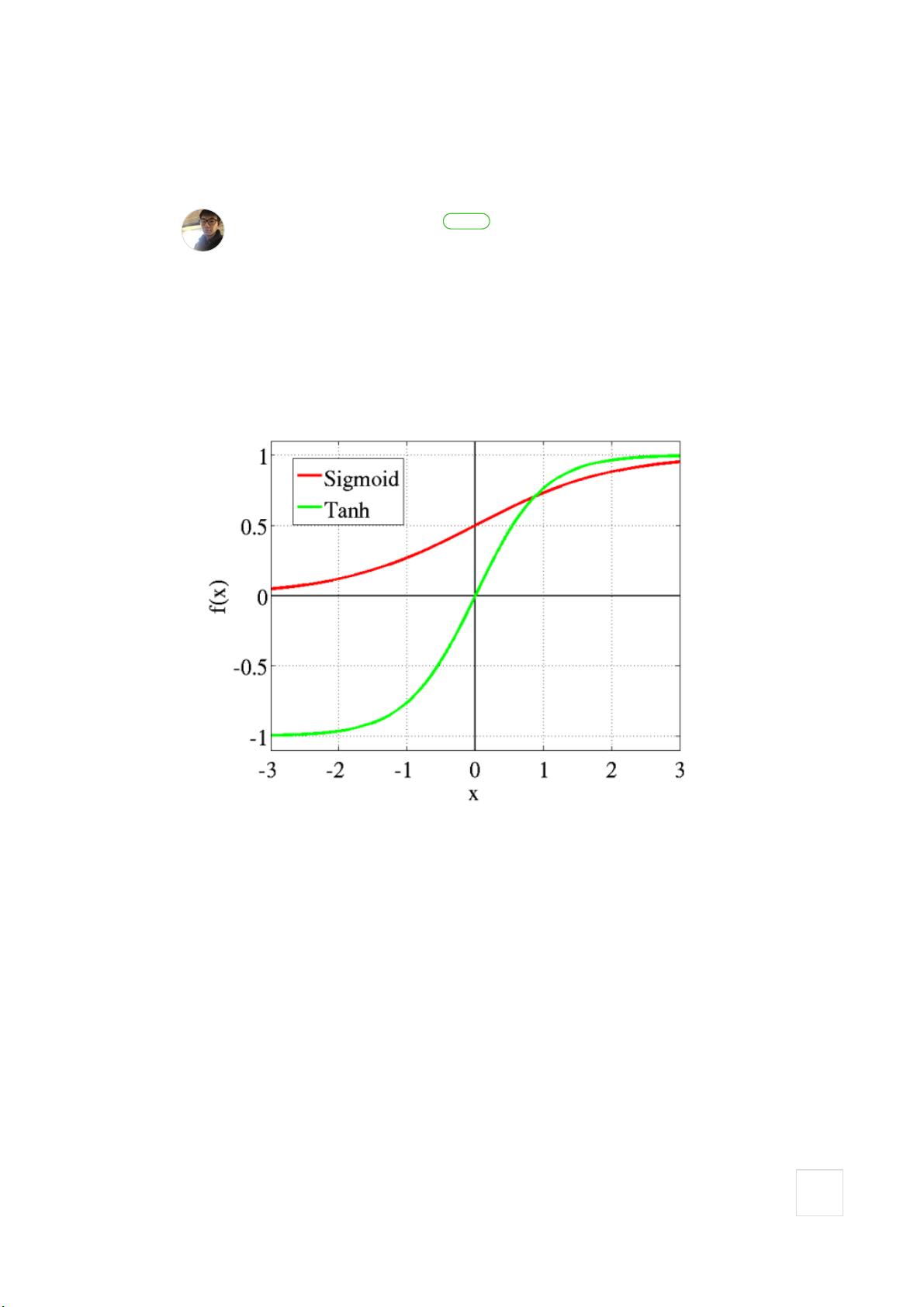
"这篇简书文章介绍了ReLU(Rectified Linear Units)激活函数，讨论了Sigmoid、Tanh等非线性激活函数的优缺点，并提到了ReLU如何缓解梯度消失问题。文章还提及了生物神经激活函数Softplus与ReLU的联系。" 在深度学习领域，激活函数是神经网络中的关键组成部分，它们引入非线性，使得神经网络能够学习更复杂的特征。ReLu，全称为Rectified Linear Units，是目前广泛使用的激活函数之一，尤其在卷积神经网络（CNNs）中表现优秀。 传统的激活函数如Sigmoid和Tanh在早期的神经网络中占据了重要地位。Sigmoid函数的输出值域在0到1之间，模拟了概率输出，且具有非线性特性，有助于特征的区分。然而，随着网络层次的增加，Sigmoid的梯度消失问题愈发严重，即在网络深层，反向传播的梯度值变得非常小，导致权重更新缓慢，训练过程近乎停滞。 相比之下，ReLU激活函数通过简单地将负值置零，保留正值不变，即f(x) = max(0, x)，显著改善了梯度消失的问题。ReLU的直截了当使其在正区间内拥有恒定的梯度1，这极大地加快了训练速度。然而，ReLU的一个缺点是可能存在“死亡ReLU”问题，即当输入为负时，梯度为0，导致某些神经元无法更新，可能在训练过程中“死亡”。 此外，为了进一步优化ReLU，出现了Leaky ReLU（LReLU）和Parametric ReLU（PReLU）。LReLU在负区间不完全置零，而是设为一个小的斜率，从而减少了死亡ReLU的发生。PReLU则更进一步，其负区间的斜率是可学习的，可以根据数据动态调整。 Softplus激活函数可以视为ReLU的平滑版本，形式为f(x) = log(1 + e^x)，它有一个连续的导数，避免了ReLU的阶跃性质可能导致的问题，但计算上稍复杂。 ReLU及其变体在解决梯度消失问题和提高训练效率方面取得了显著进展，成为了现代神经网络设计的首选激活函数。同时，这些函数的设计灵感来源于对生物神经元工作原理的理解，展现了理论与实践的结合。