循环码原理与应用：从定义到生成矩阵

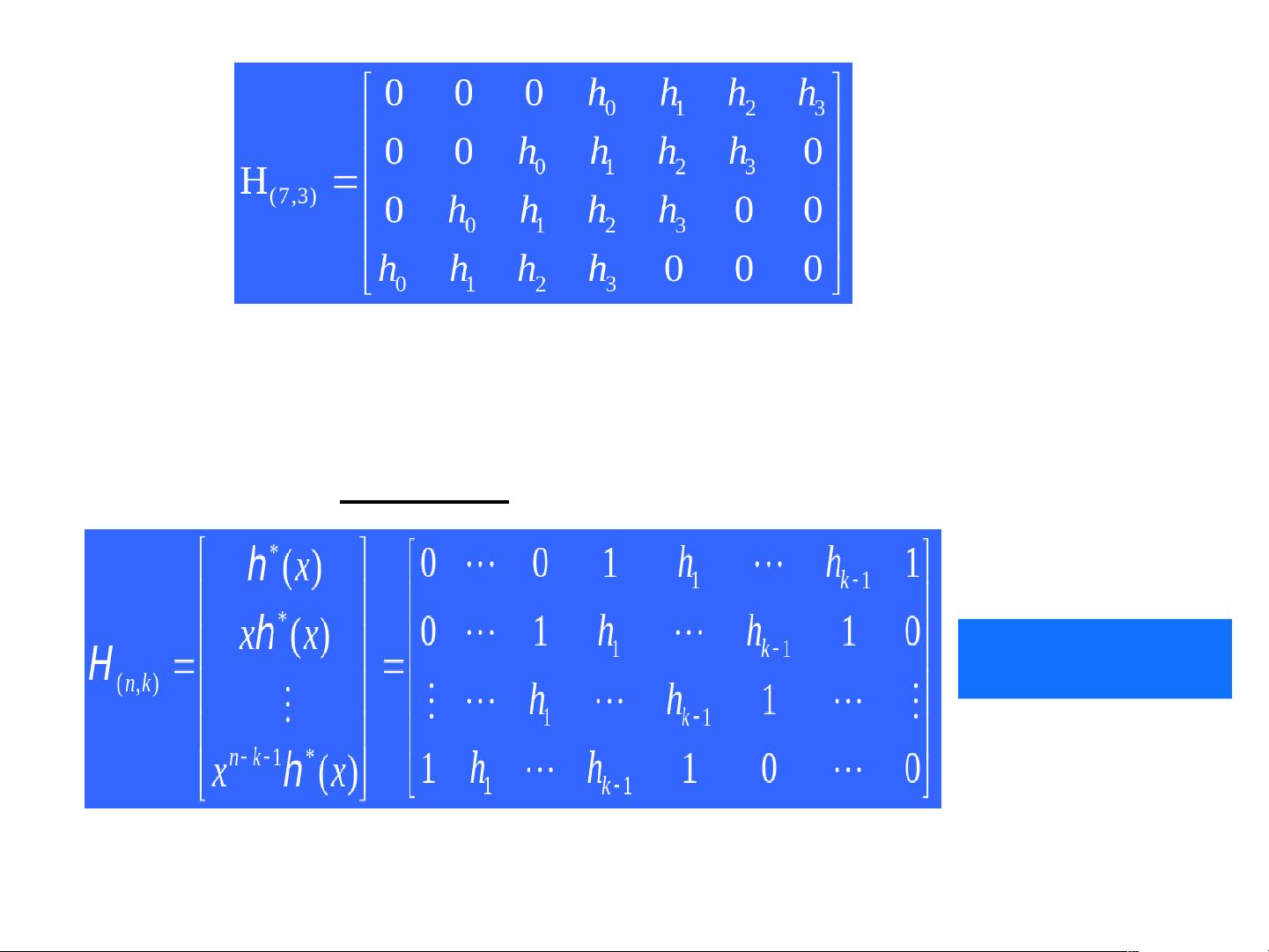
"循环线性码，特别是循环码，是一种重要的线性分组码类型，以其独特的循环性质和强大的错误检测与纠正能力而备受关注。循环码不仅具备线性码的基本特性，还允许码矢进行循环移位后仍保持有效。这种编码方式在实际应用中因其构造简单和解码效率高而广泛使用。 循环码的定义基于线性码的扩展，对于一个(n,k)线性分组码，如果它的任意码矢在进行循环移位后仍然属于码空间，那么这个码就是循环码。例如，一个n维码矢C经过i次循环移位，其码多项式可以通过乘以xi然后对xn+1取模来表示。这种方法简化了循环码的运算。 循环码通常用多项式来描述，码矢的每一个分量对应着多项式的系数。二进制循环码的码多项式所有系数仅为0或1。码多项式的循环移位可以转化为多项式乘以xi后对(xn+1)取模的过程。例如，码矢C(x)的一次循环移位C(1)(x)就是C(x)乘以x后对(xn+1)取模的结果。 生成多项式和生成矩阵是理解循环码的关键概念。生成多项式g(x)是一个n-k次的多项式，它用于生成所有可能的循环码多项式。通过g(x)以及它的循环移位，可以构建出整个(n,k)循环码的生成矩阵，这个矩阵包含了所有合法码矢的线性组合。生成矩阵的列向量是码空间中的基，码矢可以通过与生成矩阵做矩阵乘法得到。 对于解码，Berlekamp-Massey算法或Reed-Solomon算法常被用于循环码，这些算法利用了循环码的代数结构，能够在保持较低计算复杂度的同时有效地检测和纠正错误。 循环码的另一个重要应用是在卷积码中，卷积码是一种利用当前和过去的输入符号来生成输出符号的码型，它具有良好的连续错误校正性能。尽管描述较为复杂，但卷积码也可以通过类似的方法利用循环结构进行处理。 循环线性码在通信、存储等领域中有着广泛的应用，因为它们能够提供有效的错误保护机制，且其结构和运算都相对简洁。了解和掌握循环码的生成、描述以及解码方法对于理解和设计高效的数据传输系统至关重要。"