掌握树与二叉树基础:概念、结构与应用
需积分: 10 199 浏览量
更新于2024-08-02
收藏 979KB PPT 举报
在数据结构的学习中,树与二叉树是核心概念,尤其对于准备考试或考研的学生来说,理解它们至关重要。树是一种非线性数据结构,由一个根节点和若干互不相交的子树组成,每个子树本身也可以是一个树。基本概念包括:
1. 定义:树由n个结点构成,其中根节点特殊,若n=0则为空树;非根节点分为子树,每个子树也是树。结点有前驱和后继的概念,根节点没有前驱,除根外每个节点有唯一前驱,而节点的后继可能多个。
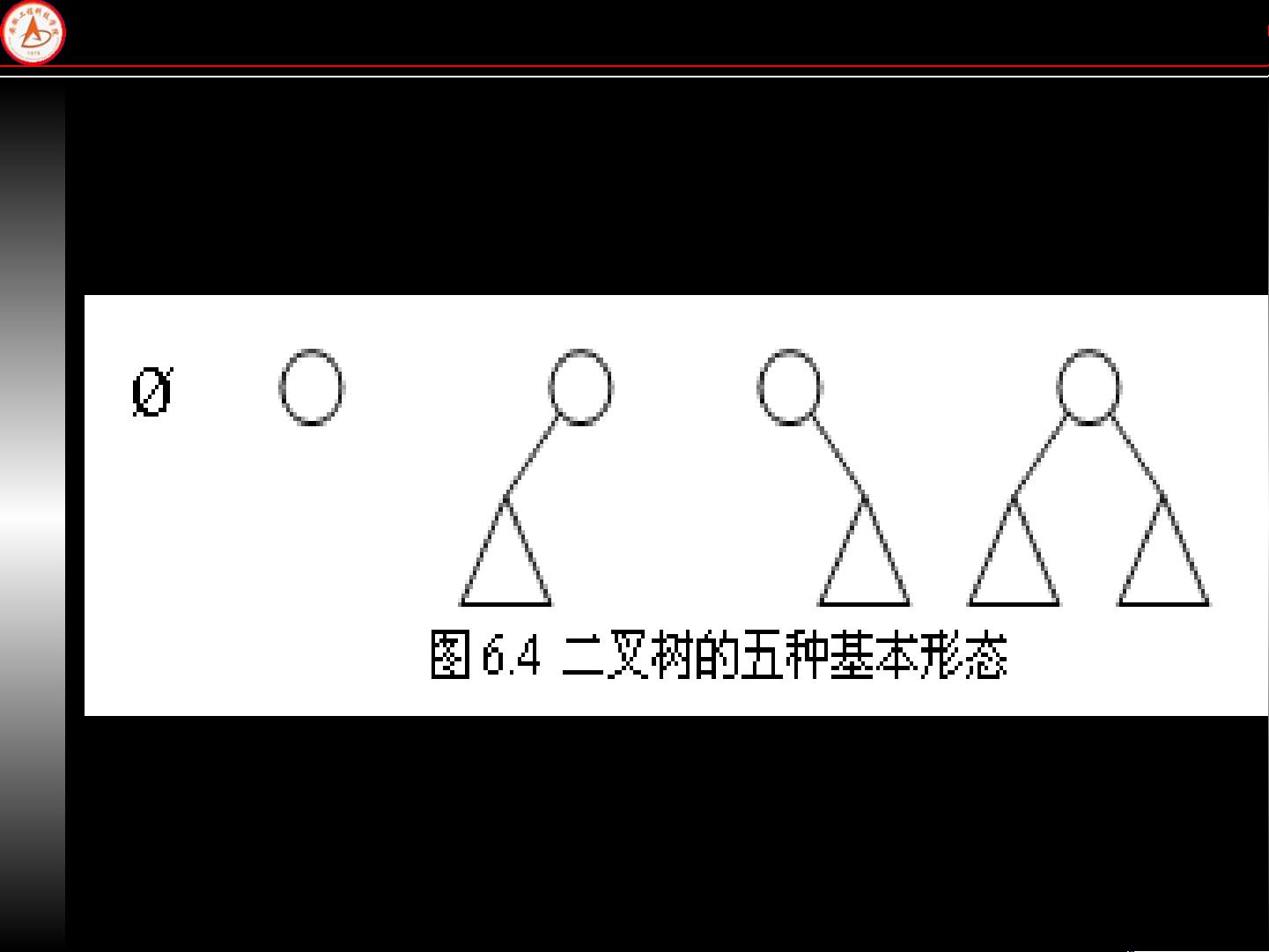
2. 结构形态:树有不同的形态,如满二叉树、完全二叉树等,这些特性会影响树的存储和遍历效率。
3. 特征:结点包含数据和指向子树的指针,度表示结点的分支数,终端结点(叶子)度为0,非终端结点度不为0。层次和深度分别指结点的层级和整个树的最大层级。
4. 有序与无序:根据子树的排列顺序,树可以分为有序树(如二叉搜索树)和无序树(数据没有特定排序)。
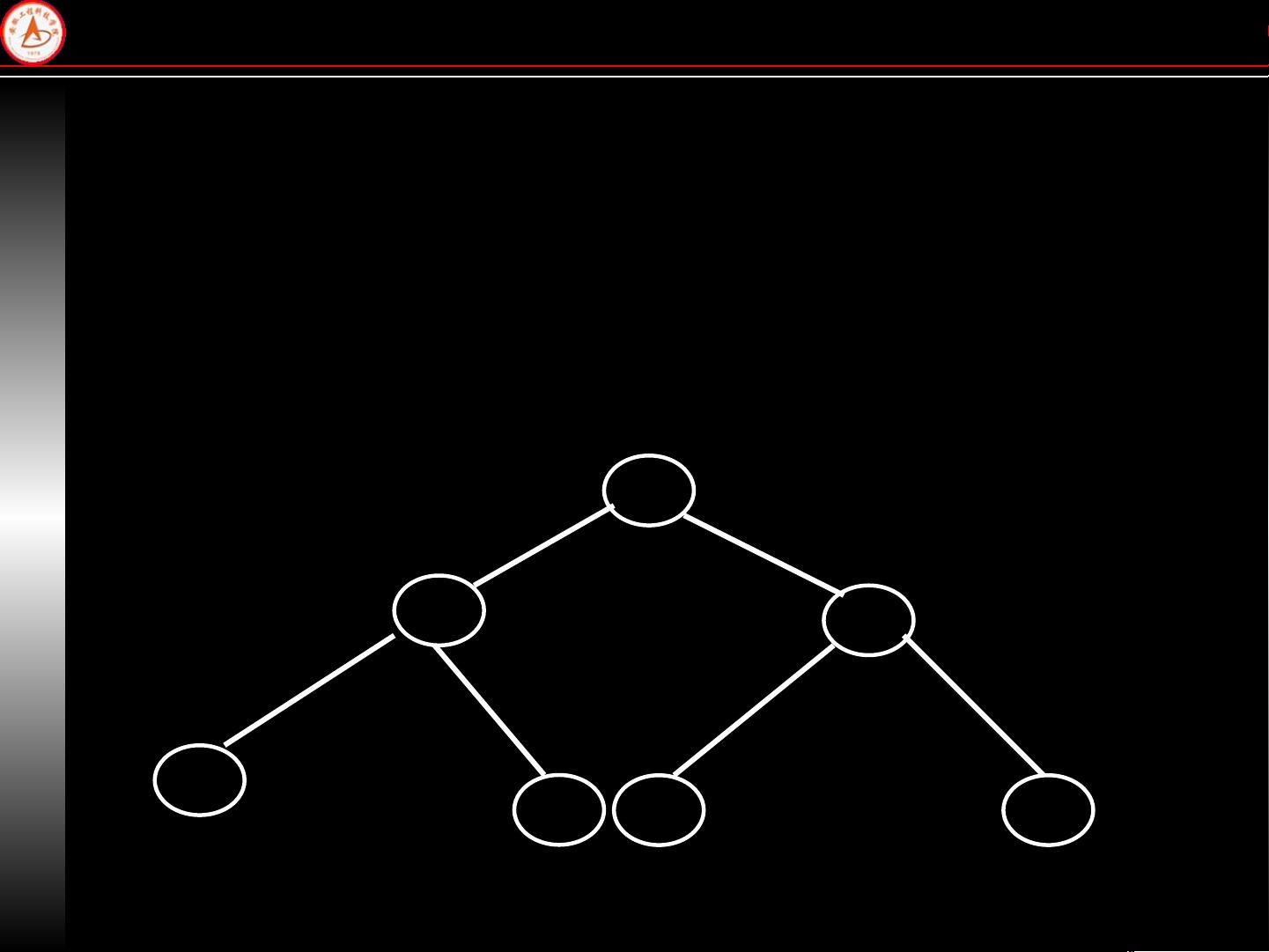
二叉树是特殊的树,每个节点最多有两个子节点,通常分为左子树和右子树。二叉树的特点和操作更为细化:
- 二叉树概念:根节点、左孩子和右孩子,度为2的结点称为满二叉树,度为1或0的结点分别称为单支树和叶子。
- 逻辑结构:递归和非递归遍历算法,如前序、中序、后序遍历,以及线索化技术提高遍历效率。
- 二叉树与树的关系:二叉树是树的一种特例,而森林则是由多个树组成的结构。
- Huffman树(最优二叉树)与Huffman编码:这是一种用于数据压缩的特殊二叉树,通过构建带权路径长度最短的二叉树,实现数据编码。
教学重点集中在二叉树的基础概念、遍历算法、线索化技术以及它们在实际问题中的应用,如Huffman编码。而教学难点主要在于非递归遍历的实现、线索化的理解以及如何构建并优化Huffman树。
掌握树和二叉树的知识,不仅有助于理解数据结构的基本原理,还能应用于实际的编程问题解决,是数据结构学习的重要组成部分。在备考过程中,深入理解这些概念并进行练习,能够显著提升算法理解和编程能力。
1114 浏览量
175 浏览量
409 浏览量
156 浏览量
113 浏览量
110 浏览量
228 浏览量
160 浏览量
yang7531388
- 粉丝: 15
- 资源: 16
最新资源
- 10-Days-of-[removed]该存储库包含针对Hackerrank的10天Javascript挑战的代码解决方案
- 初级java笔试题-jwasham:杰瓦萨姆
- commons-net-jar包.zip
- seed-datepicker:Seed框架的可自定义的datepicker组件
- Bloc_Api_token
- lxdfile:LXD容器的类似于Dockerfile的文件格式
- 蔬菜品种的分类——果菜类
- Unity 2018.1 中文手册 中文文档
- pugsql:一个受HugSQL启发的Python数据库库
- 人机交互项目
- abpMVC.zip
- 生鲜商品:超市生鲜食品经营要求
- Shipped.io Iraq-crx插件
- Machine-Learning-Project:机器学习天气对酒点的影响
- ENV Alert - 本番環境で警告表示-crx插件
- lain:Rust内置的Fuzzer框架