Python实现迪杰斯特拉(Dijkstra)算法详解

"本文主要介绍了Python实现狄克斯特拉算法的过程和步骤，以及如何通过代码进行实际操作。" 狄克斯特拉算法(Dijkstra's algorithm)是由荷兰计算机科学家艾兹格·迪科斯彻提出的一种寻找有向图中单源最短路径的算法。在IT领域，这种算法广泛应用于网络路由、地理信息系统以及任何需要找到两点间最短路径的问题。本文将详细阐述狄克斯特拉算法的工作原理，并提供一个Python实现的例子。 一、算法简介 狄克斯特拉算法的核心思想是从起点开始，逐步找到到达各个节点的最短路径。它维护一个优先队列（通常使用二叉堆实现），用于存储待处理的节点，优先队列中的节点按照当前已知的最短路径长度排序。算法不断从队列中取出距离起点最近的节点，更新其邻居节点的最短路径，直到所有节点都被处理。 二、算法步骤 1. 初始化：设置所有节点的最短路径为无穷大，除了起点的最短路径设为0；同时记录每个节点的前驱节点（即到达该节点的路径来源）。 2. 将起点加入优先队列。 3. 每次从优先队列中取出当前最短路径长度的节点，遍历其所有邻居，如果通过该节点到达邻居的路径更短，则更新邻居的最短路径长度和前驱节点。 4. 将更新后的邻居节点加入优先队列。 5. 重复上述过程，直到优先队列为空，即所有节点都被处理过。 6. 最终，通过前驱节点记录的路径可以重建从起点到任意节点的最短路径。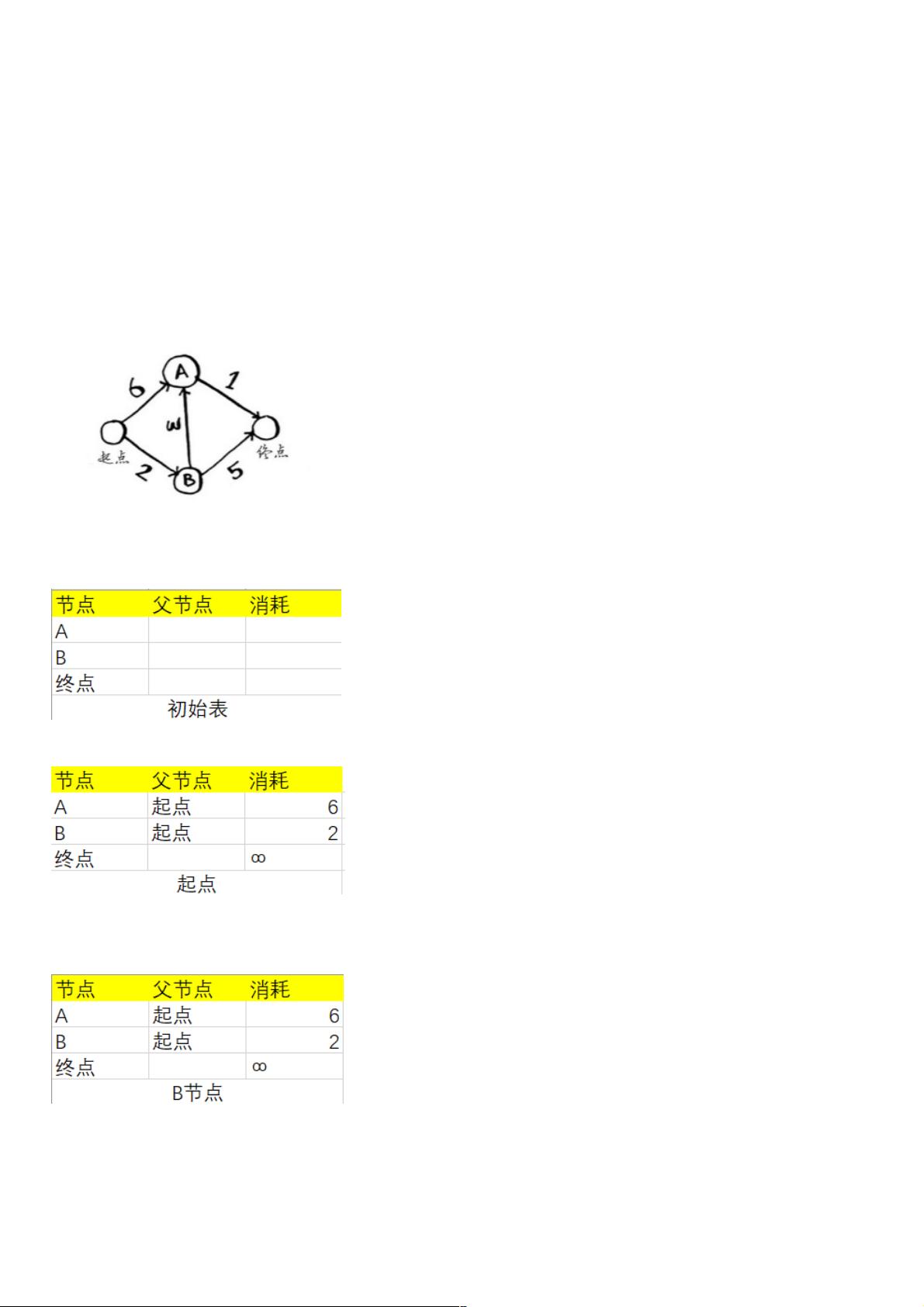 三、图解示例 以包含5个节点的有向图为例，每个节点之间的边表示消耗的时间。算法开始时，首先创建一个初始表，记录从起点到每个节点的最短路径。然后，按照算法步骤更新节点状态，每次选择当前最短路径的节点，更新其邻居节点，直到找到终点的最短路径。 四、Python代码实现 在Python中，可以使用字典来表示图和节点的开销，同时利用heapq库实现优先队列。以下是一个简单的代码实现： ```python import heapq def dijkstra(graph, start): costs = {node: float('inf') for node in graph} costs[start] = 0 parents = {node: None for node in graph} queue = [(0, start)] while queue: current_cost, current_node = heapq.heappop(queue) if current_cost > costs[current_node]: continue for neighbor, weight in graph[current_node].items(): path_cost = current_cost + weight if path_cost < costs[neighbor]: costs[neighbor] = path_cost parents[neighbor] = current_node heapq.heappush(queue, (path_cost, neighbor)) return costs, parents # 示例图 graph = { 'start': {'a': 6, 'b': 2}, 'a': {'end': 1}, 'b': {'a': 3, 'end': 5}, 'end': {} } costs, parents = dijkstra(graph, 'start') ``` 在这个例子中，`dijkstra`函数接收一个字典表示的图和起始节点，返回每个节点的最短路径成本和前驱节点信息。通过调用这个函数，我们可以找到从"start"到"end"的最短路径和其成本。 五、总结 狄克斯特拉算法是解决有向图单源最短路径问题的高效方法，尤其适用于权值非负的情况。通过理解算法的原理和实现，我们可以将其应用到各种实际场景中，例如优化网络路由、路径规划等。在Python中，利用数据结构和库支持，我们可以轻松地实现并运行这个算法。