1416 IEEE TRANSACTIONS ON INDUSTRY APPLICATIONS, VOL. 45, NO. 4, JULY/AUGUST 2009
Analysis of Double-Star Permanent-Magnet
Synchronous Generators by a General
Decoupled
d–q Model
Mauro Andriollo, Giulio Bettanini, Giovanni Martinelli, Augusto Morini, and Andrea Tortella
Abstract—This paper proposes a technique to analyze double-
star permanent-magnet synchronous generators by transforming
the two three-phase winding sets into two couples of windings on
the d-andq-axes of the rotor reference frame. The technique
introduces improvements with respect to other approaches, as
it takes into account the harmonic content of the no-load flux
linkages of the armature windings, it applies to a generic angular
displacement between the two winding sets, and it greatly sim-
plifies the analysis since the two transformed winding sets are
decoupled with respect to each other.
Index Terms—Electric machine modeling, permanent-magnet
(PM) machines, windings.
I. INTRODUCTION
I
N THE frame of the growing utilization of distributed
generation and, in particular, of the renewable sources and
of the industrial and agricultural by-products and wastes, low-
and medium-rating permanent-magnet synchronous generators
(PMSGs) meet with increasing application. Although the three-
phase winding configurations are dominant, nevertheless, the
double-star windings offer several benefits in terms of lower dc-
link current/voltage ripple, lower torque pulsation (particularly
critical in systems driven by high speed microturbines), and
higher reliability. Furthermore, the series–parallel connection
of the rectified outputs of two distinct three-phase groups may
represent a favorable option for a variable-speed wind-turbine-
driven generation system.
The proposed technique analyzes the double-star PMSG by
transforming the stator three-phase winding sets {1
, 2
, 3
}
and {1
, 2
, 3
} (Fig. 1) into two couples of windings on the
d- and q-axes of the rotor reference frame. With respect to
other approaches [1]–[4], the methodology offers the following
improvements.
1) It takes into account the harmonic content of the no-load
flux linkages of the armature windings.
2) It applies to a generic angular displacement 2α between
the two winding sets.
Paper 2008-EMC-042.R1, presented at the 2007 IEEE International Electric
Machines and Drives Conference, Antalya, Turkey, May 3–5, and approved
for publication in the IEEE T
RANSACTIONS ON INDUSTRY APPLICATIONS
by the Electric Machines Committee of the IEEE Industry Applications Society.
Manuscript submitted for review July 23, 2008 and released for publication
February 19, 2009. First published June 2, 2009; current version published
July 17, 2009.
The authors are with the Department of Electrical Engineering, University
of Padova, 35131 Padova, Italy (e-mail: mauro.andriollo@unipd.it; giulio.
bettanini@unipd.it; giovanni.martinelli@unipd.it; augusto.morini@unipd.it;
andrea.tortella@unipd.it).
Digital Object Identifier 10.1109/TIA.2009.2023553
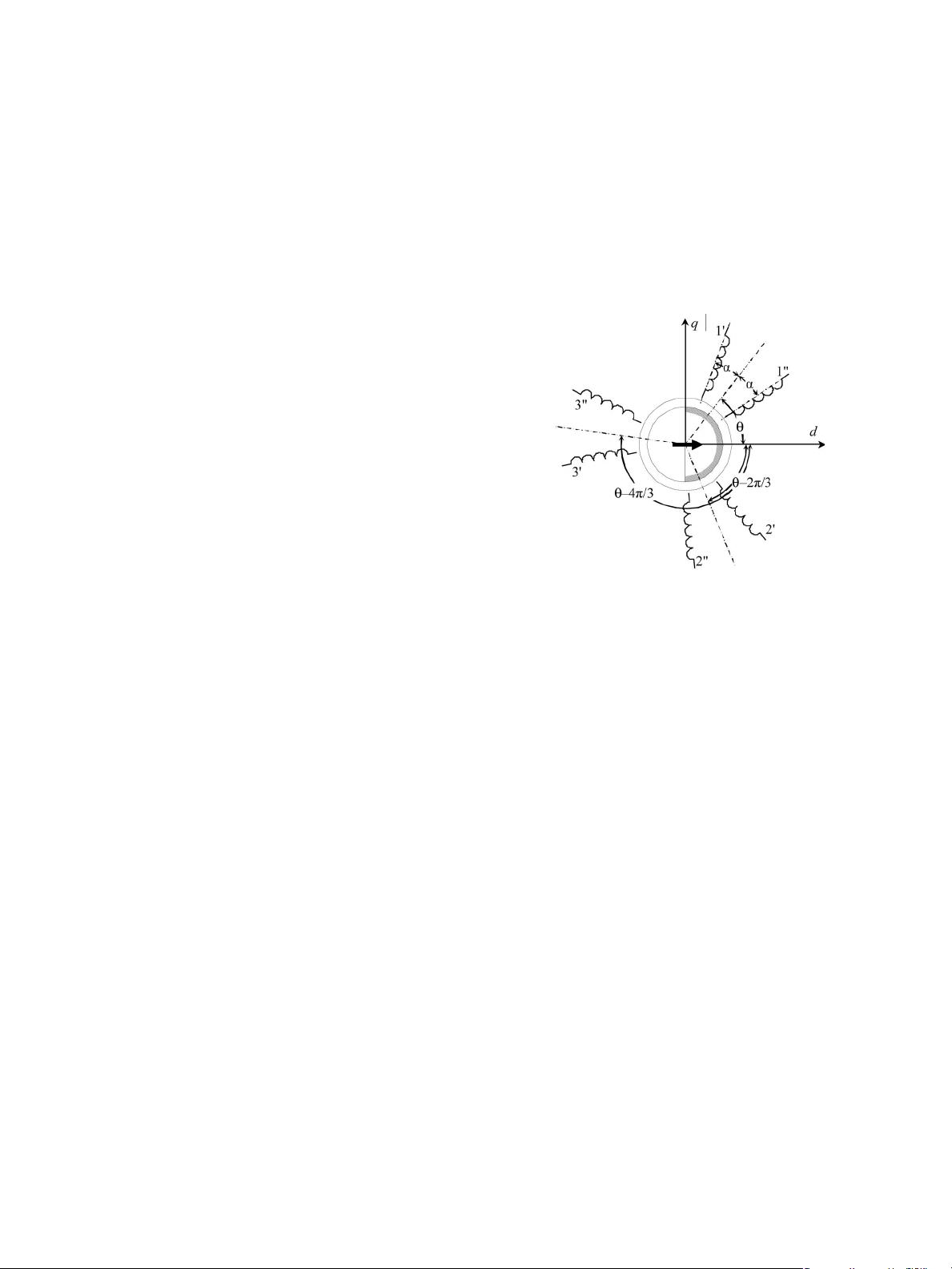
Fig. 1. Winding arrangement and definition of angular quantities (θ: rotor
position expressed by the angle between the d-axis and the 1
− 1
phase axes
bisector).
3) It greatly simplifies the analysis since the two trans-
formed winding sets are decoupled with respect to each
other.
II. D
ESCRIPTION OF THE METHOD
In the hypotheses of equal symmetrical three-phase wind-
ings, rotor isotropic magnetic structure, and negligible satu-
ration effects, the following equalities hold for the armature
inductances:
L
1
1
= L
2
2
= L
3
3
= L
1
1
= L
2
2
= L
3
3
= L
s
M
1
2
= M
2
3
= M
3
1
= M
1
2
= M
2
3
= M
3
1
= M
s
M
1
1
= M
2
2
= M
3
3
= M
a
M
1
2
= M
2
3
= M
3
1
= M
b
M
1
3
= M
2
1
= M
3
2
= M
c
. (1)
Let δ = θ ± α be the angular displacement of the axis of the
reference stator winding (1
or 1
) with respect to the d-axis,
and let λ
fs
(δ) be its no-load flux linkage due to the permanent
magnets (PMs). To evaluate the winding voltages, the PMs
can be replaced by an equivalent rotor winding supplied by a
constant current I
f
, where M
fs
(δ)=λ
fs
(δ)/I
f
is the mutual
inductance with the stator winding, and L
f
(θ)=λ
f
(θ)/I
f
is
0093-9994/$25.00 © 2009 IEEE









