Simulink模拟振动系统：单自由度无阻尼振动分析

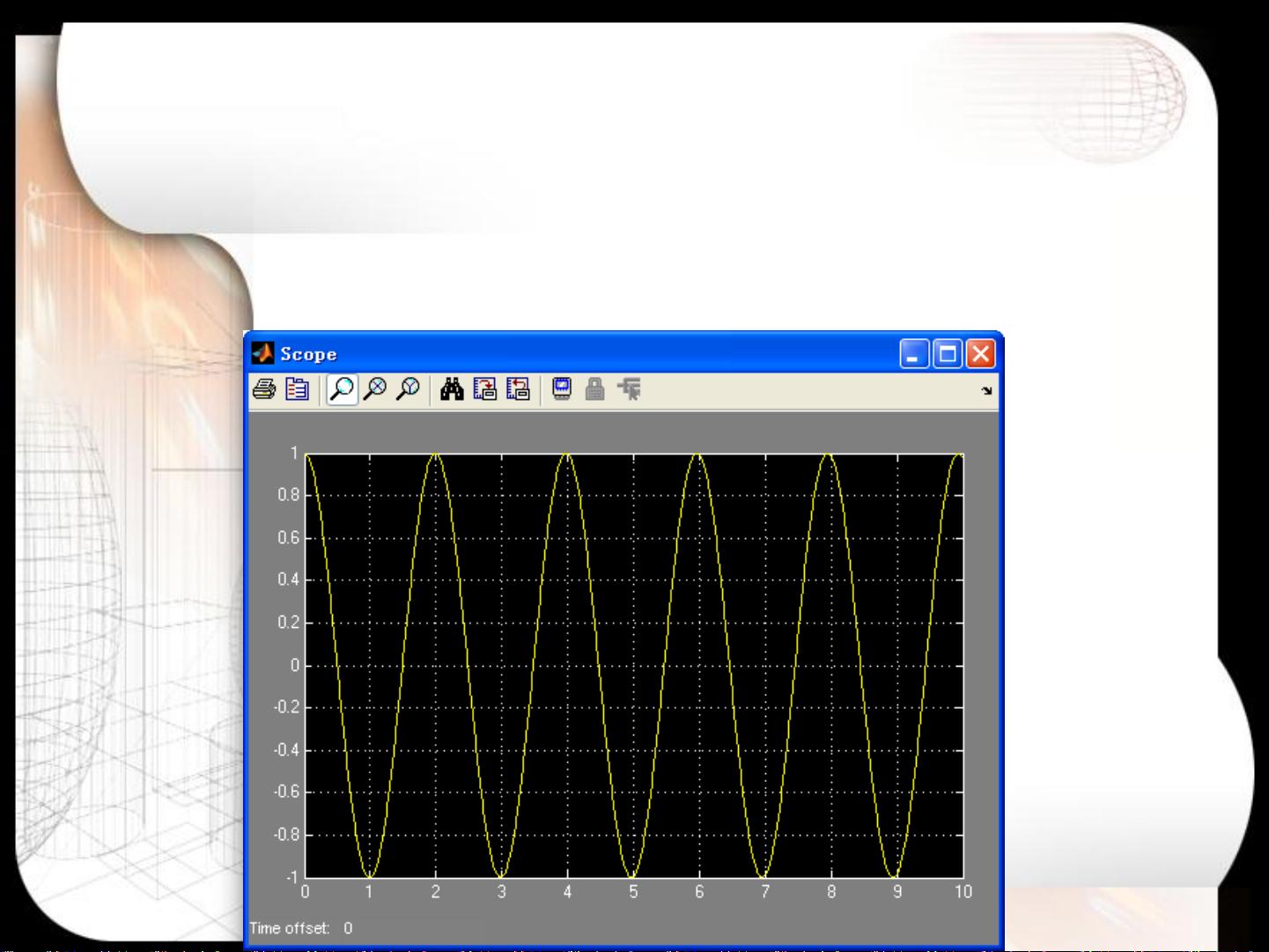
"Simulink机械振动仿真简例" 在Simulink中进行机械振动仿真是一项重要的工程实践，它可以帮助我们理解和分析动态系统的响应。Simulink是MATLAB环境中的一个强大工具，它提供了对连续系统、离散系统以及混合系统的建模、仿真和分析功能。在机械振动领域，Simulink可以用来模拟各种振动现象，例如单自由度无阻尼自由振动。 首先，我们来看单自由度无阻尼自由振动的例子。这是一个基础的弹簧-质量系统，其中质量m受到弹簧力kx的影响，根据牛顿第二定律，系统满足微分方程m * x'' + k * x = 0。在这个例子中，x代表位移，x''是加速度。为了在Simulink中构建这个模型，我们需要设定合适的参数，如k和m，并确定初始状态，比如初始位移和速度。通过设置乘法器的值（-k/m）和积分器的初始条件，我们可以得到振动的仿真结果。如果发现曲线不光滑，可能是因为时间步长设置过大，可以通过减小最大步长来提高仿真精度，从而获得更平滑的振动曲线。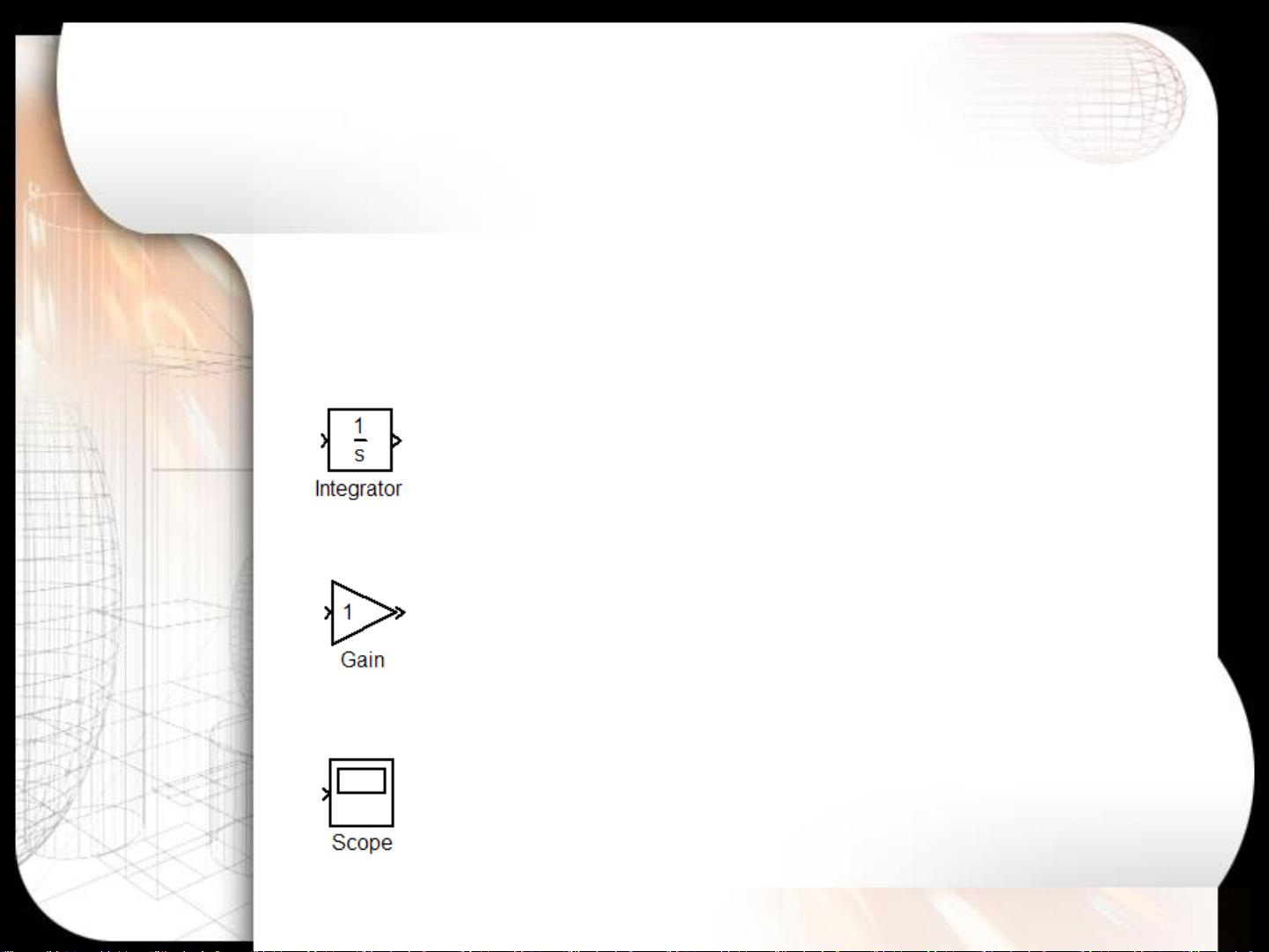 在Simulink的仿真过程中，常用的模块包括积分器（用于数值积分），增益模块（调整信号强度），以及示波器模块（展示仿真结果）。这些模块的组合使用能帮助我们直观地观察和理解振动系统的动态行为。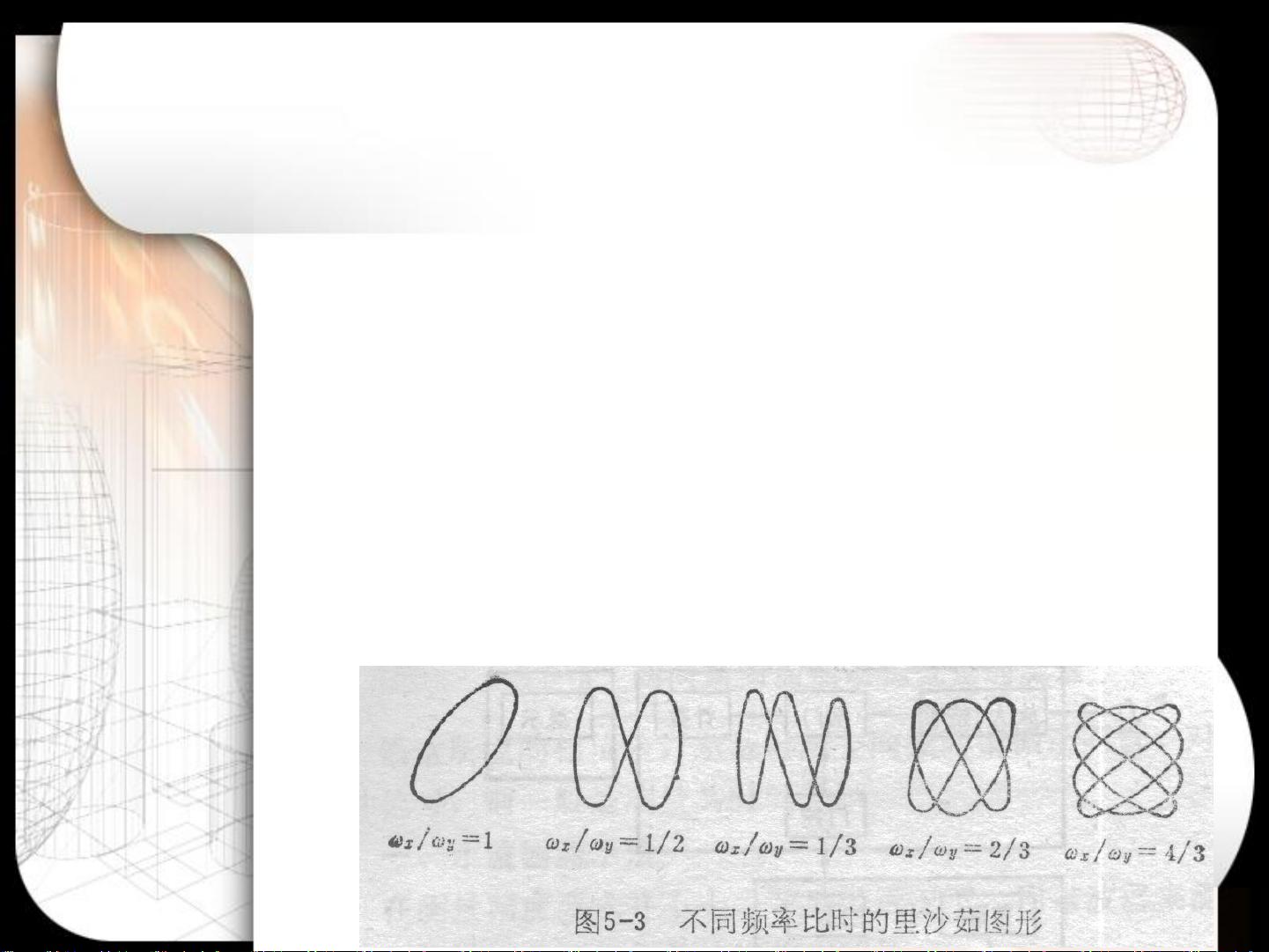 接下来，我们讨论了简谐波形的里沙茹图形分析。里沙茹图形是当两个简谐振动信号在示波器上叠加时产生的稳定轨迹。如果这两个信号的频率比是正有理数，那么示波器上会出现特定的图形，例如椭圆。这个原理在频谱分析和信号处理中非常有用，因为它可以揭示信号之间的频率关系。当两个信号的相位差为90度时，形成的图形是正椭圆。通过观察里沙茹图，我们可以直接读出两个信号的频率比，这对于识别和测量复杂的振动模式非常有帮助。 Simulink的机械振动仿真不仅能够帮助工程师理解基本的振动理论，还能应用于更复杂系统的研究，如多自由度振动、有阻尼振动以及非线性振动等。通过这种可视化的方法，我们可以直观地模拟和分析振动系统的行为，从而优化设计，预测性能，以及解决实际工程问题。