ACM竞赛入门：深度解析线段树及其应用

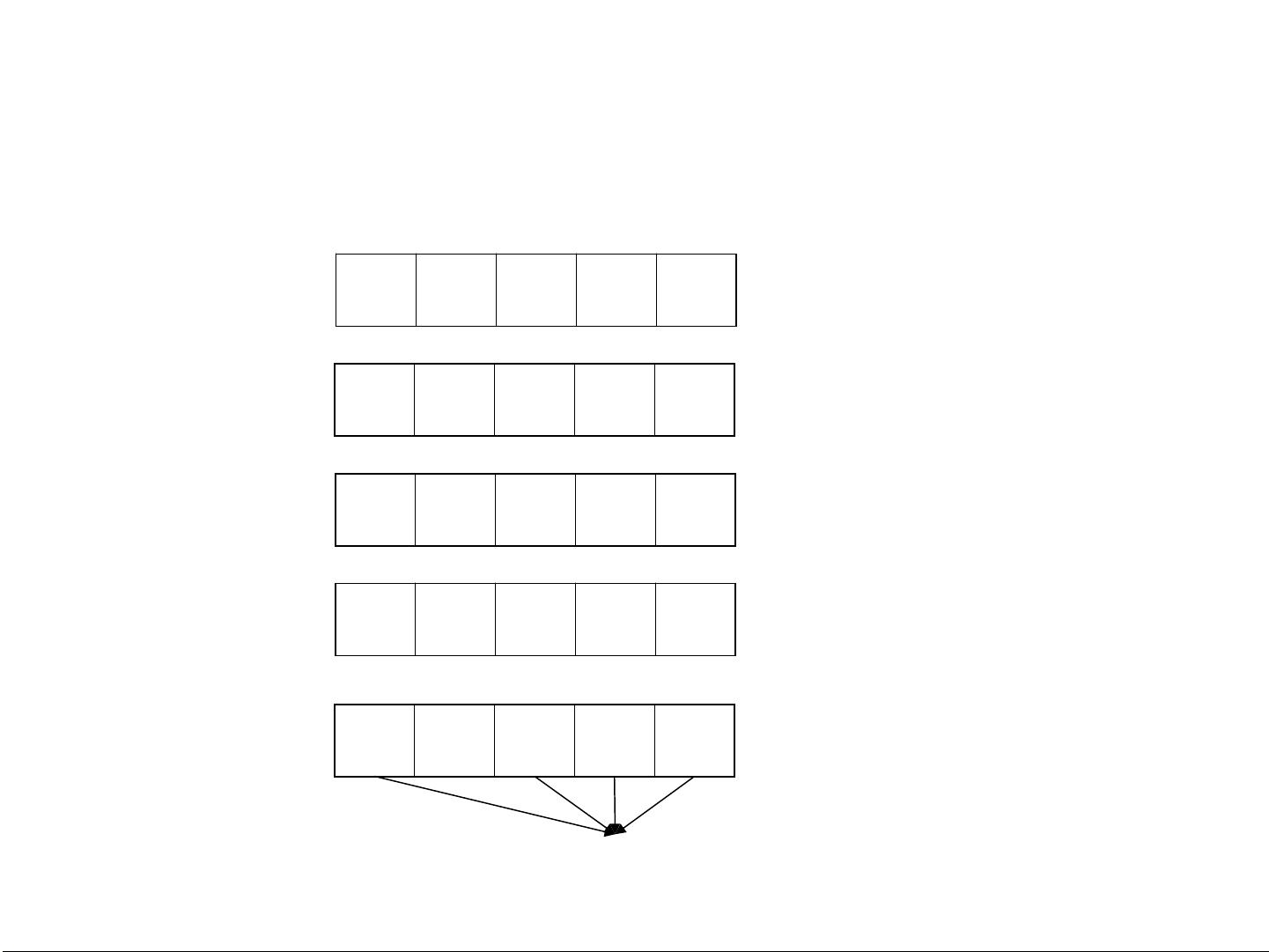
线段树是一种高效的数据结构，特别适用于解决与区间相关的动态查询问题，在ACM程序设计竞赛中被广泛应用。它是一种二叉树结构，用于对区间进行组织和操作，使得我们可以快速进行诸如区间长度求和、区间个数计算等任务。 在浙江大学ACM校队的教程中，线段树的基本构造思想是通过递归构建。每个节点代表一个区间，叶子节点表示长度为1的区间，非叶节点的左右子节点分别代表区间的左右半部分。这种划分方式使得查询区间内的信息可以通过路径查询在树中高效地实现。例如，一个区间 [1,10] 在线段树中会被拆分为 [1,5], [5,10], [1,3], [3,5], [5,7] 等更小的区间，便于存储和处理。 线段树的每个节点除了包含原始区间的信息外，还会附加一些额外域，这些域通常用来存储动态维护的统计数据，比如区间长度的和或个数。这种灵活性使得线段树能够适应不同的问题需求，提高了算法的效率。 在解决实际问题时，比如题目中提到的关于盒子投影长度的问题，线段树可以帮助我们快速计算所有盒子投影在墙上的影子的总宽度。通过将线段的起始和结束坐标离散化，排序后与顺序号关联，我们可以用线段树来替代直接遍历所有可能的区间，大大减少时间复杂度，避免在区间范围很大时导致效率低下。 传统的解决方案是用一个一维数组来存储每个区间是否被遮挡，然后通过遍历数组计算1的个数，但这种方法的时间复杂度是O(n^2)，当区间数量较大时效率较低。相比之下，线段树的方法通常能提供线性或者接近线性的查询时间复杂度，O(logn)，这对于解决大规模数据问题具有显著优势。 线段树作为ACM编程中的一个重要工具，不仅帮助参赛者理解和处理区间问题，还能提升算法的性能，对于提升竞赛中的竞争力具有重要作用。学习和掌握线段树是ACM初学者不可或缺的一部分。