JPEG压缩标准详解：基础与核心技术

需积分: 12 178 浏览量更新于2024-07-16 收藏 77KB PDF 举报

"JPEG图片压缩标准" JPEG（Joint Photographic Experts Group，联合图像专家组）是一种广泛使用的图像压缩标准，由ISO和CCITT（现在的ITU-T）联合制定。这个标准首次在1991年4月的《ACM通讯》上发布，并在此后进行了修订。JPEG的目标是创建一个通用的压缩标准，适用于灰度和彩色的连续色调静止图像，以适应各种不同的应用需求。该标准包含两种基本的压缩方法：基于ADCT（离散余弦变换）的"有损"压缩方法和基于预测的"无损"压缩方法。有损压缩通常会导致图像质量的轻微下降，但能实现更高的压缩率，适合存储空间有限的情况。无损压缩则保留所有原始数据，压缩后可以完全恢复原始图像，但压缩比相对较低。其中，基础线方法（Baseline method）是JPEG标准中最简单且被最广泛实施的有损压缩技术，它是其他DCT模式的一个子集。基础线方法通过执行一系列步骤，包括颜色空间转换（通常从RGB到YCbCr）、8x8像素块的离散余弦变换、量化和熵编码，来降低图像数据的冗余。量化过程是造成图像质量损失的关键步骤，因为它会舍弃一些对人眼感知影响较小的高频信息。基础线方法的压缩程度可以通过调整量化表来控制，这允许用户在压缩率和图像质量之间进行权衡。对于许多应用来说，基础线方法已经足够满足需求，尤其是在网络传输和存储限制较大的场景下。 JPEG标准还支持自定义选项，如不同的色度采样率，这可以根据图像内容和应用需求来优化压缩效果。此外，JPEG还提供了用于编码图像元数据的框架，如EXIF信息，这对于照片的管理和编辑非常重要。总结来说，JPEG图片压缩标准提供了一套灵活且高效的图像压缩方案，其基础线方法在平衡压缩效率和图像质量方面表现出色。尽管随着技术的发展，新的压缩标准如JPEG 2000和WebP等相继出现，但原始的JPEG标准仍然在很多领域得到广泛应用，特别是在互联网和数字摄影中。

typically vary slowly from point to point across an

image, the FDCT processing step lays the foundation

for achieving data compression by concentrating most

of the signal in the lower spatial frequencies. For a

typical 8x8 sample block from a typical source image,

most of the spatial frequencies have zero or near-zero

amplitude and need not be encoded.

At the decoder the IDCT reverses this processing step.

It takes the 64 DCT coefficients (which at that point

have been quantized) and reconstructs a 64-point ouput

image signal by summing the basis signals.

Mathematically, the DCT is one-to-one mapping for

64-point vectors between the image and the frequency

domains. If the FDCT and IDCT could be computed

with perfect accuracy and if the DCT coefficients were

not quantized as in the following description, the

original 64-point signal could be exactly recovered. In

principle, the DCT introduces no loss to the source

image samples; it merely transforms them to a domain

in which they can be more efficiently encoded.

Some properties of practical FDCT and IDCT

implementations raise the issue of what precisely

should be required by the JPEG standard. A

fundamental property is that the FDCT and IDCT

equations contain transcendental functions.

Consequently, no physical implementation can

compute them with perfect accuracy. Because of the

DCT’s application importance and its relationship to

the DFT, many different algorithms by which the

FDCT and IDCT may be approximately computed have

been devised [16]. Indeed, research in fast DCT

algorithms is ongoing and no single algorithm is

optimal for all implementations. What is optimal in

software for a general-purpose CPU is unlikely to be

optimal in firmware for a programmable DSP and is

certain to be suboptimal for dedicated VLSI.

Even in light of the finite precision of the DCT inputs

and outputs, independently designed implementations

of the very same FDCT or IDCT algorithm which differ

even minutely in the precision by which they represent

cosine terms or intermediate results, or in the way they

sum and round fractional values, will eventually

produce slightly different outputs from identical inputs.

To preserve freedom for innovation and customization

within implementations, JPEG has chosen to specify

neither a unique FDCT algorithm or a unique IDCT

algorithm in its proposed standard. This makes

compliance somewhat more difficult to confirm,

because two compliant encoders (or decoders)

generally will not produce identical outputs given

identical inputs. The JPEG standard will address this

issue by specifying an accuracy test as part of its

compliance tests for all DCT-based encoders and

decoders; this is to ensure against crudely inaccurate

cosine basis functions which would degrade image

quality.

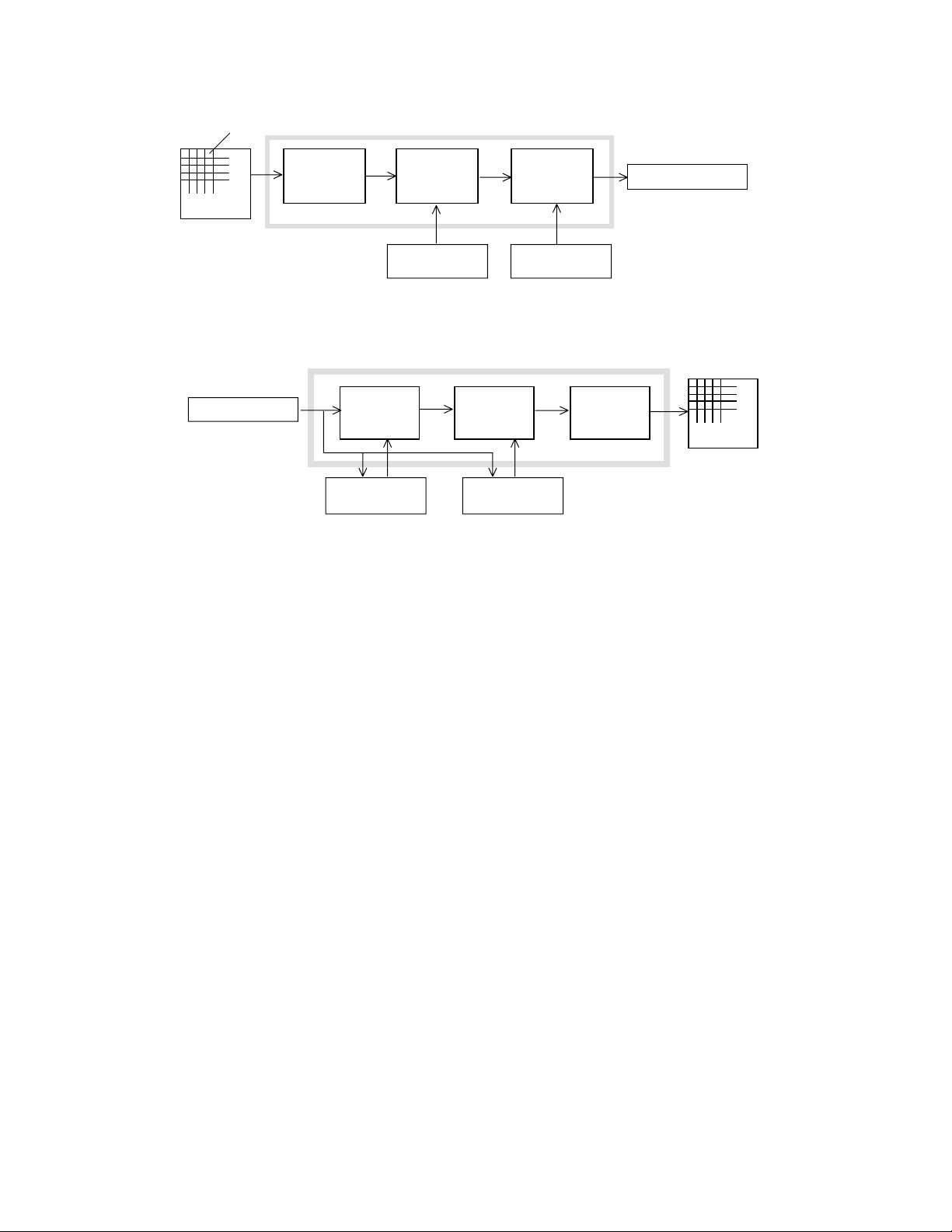
8x8 blocks DCT-Based Encoder

FDCT Quantizer

Entropy

Encoder

Source Table Table Compressed

•

Specifications Image Data

Specifications

Image Data

Entropy

Decoder

Dequantizer IDCT

DCT-Based Decoder

Table Table

Specifications Specifications

Compressed

Image Data

Reconstructed

Image Data

Figure 1. DCT-Based Encoder Processing Steps

Figure 2. DCT-Based Decoder Processing Steps

剩余16页未读，继续阅读

字由人

粉丝: 28
资源: 35

JPEG压缩标准详解：基础与核心技术

JPEG图像压缩算法

JPEG图片压缩程序(1/5)

JPEG静态图片压缩标准

JPEG图片压缩软件

JPEG -recompress Linux JPEG图片压缩工具

jpeg图片压缩库jpeg-9b

JPEG压缩标准

JPEG图片压缩jpopt3.rar

静态JPEG图像压缩标准.ppt

JPEG -recompress Windows x86 64位 JPEG图片压缩工具包

最新资源