马尔可夫决策过程：理论与应用

马尔可夫决策过程（Markov Decision Process, MDP）是一种在计算机科学中广泛应用的数学模型，用于处理那些决策者能够控制部分随机环境中的问题。MDPs由四个关键元素组成：状态集E、动作集A、转移概率分布Pr和奖励函数R。以下是这些元素的详细解释： 1. **状态集** (States, E): MDP中的环境由一组完全可观测的状态集合E构成，每个状态代表一个特定的系统或情境。例如，在一个游戏或机器人控制的环境中，状态可能包括棋盘位置、游戏关卡或机器人的传感器读数。 2. **动作集** (Actions, A): 动作集A定义了在每个状态下可以执行的一系列操作或决策，比如移动、选择菜单选项或执行特定操作。 3. **转移概率分布** (Transition Probability, Pr): 这是一个家庭式函数 {Pr(e, a, e') | e ∈ E, a ∈ A(e)}，表示在执行动作a后从状态e转移到状态e'的概率。这是一个关键特性，因为它反映了决策对环境动态的影响不确定性。 4. **奖励函数** (Reward Function, R): R是将每个状态映射到实数的函数，R(e)表示处于状态e时立即获得的奖励。它是MDP的核心目标导向，决策者的策略通常是为了最大化长期累积的奖励。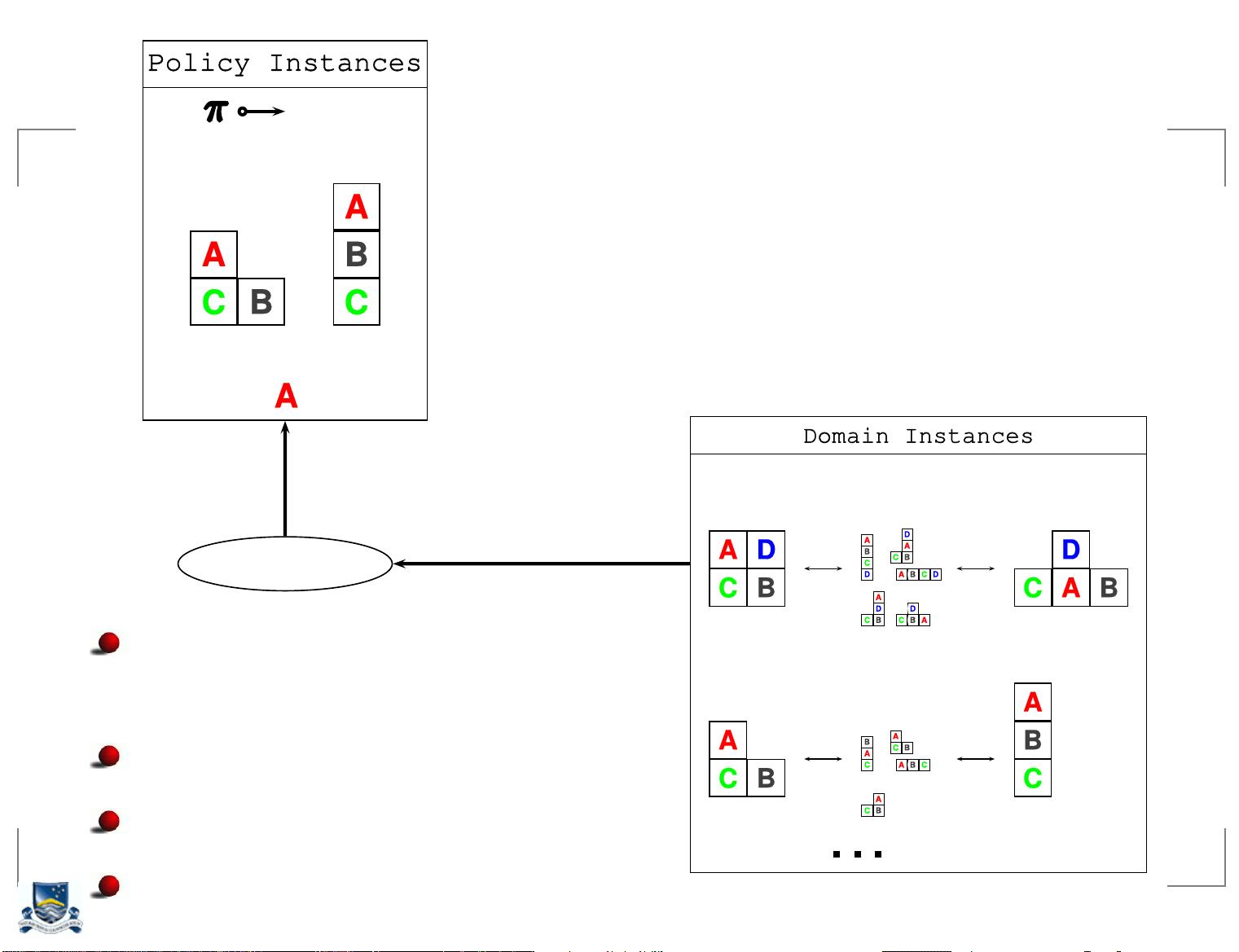 5. **策略** (Policy, π): 一个策略π是从状态E到动作A的映射，即π(e)给出在状态e下应采取的动作。策略可以是确定性的，即总是选择同一个动作，也可以是随机的。 6. **价值函数** (Value Function, Vπ): 给定策略π，每个状态的价值Vπ(e)是其长期期望累计奖励。Vπ(e)通过递归地计算未来奖励的期望值来确定，公式为Vπ(e) = lim(n→∞) E[Σ(γ^t * R(et)) | π, e0 = e]，其中γ是折扣因子，用于考虑未来奖励的重要性。 7. **最优策略** (Optimal Policy): 如果一个策略π满足对于所有状态e和所有其他策略π'，Vπ(e) ≥ Vπ'(e)，那么π就是最优策略，因为它提供了最大的长期期望收益。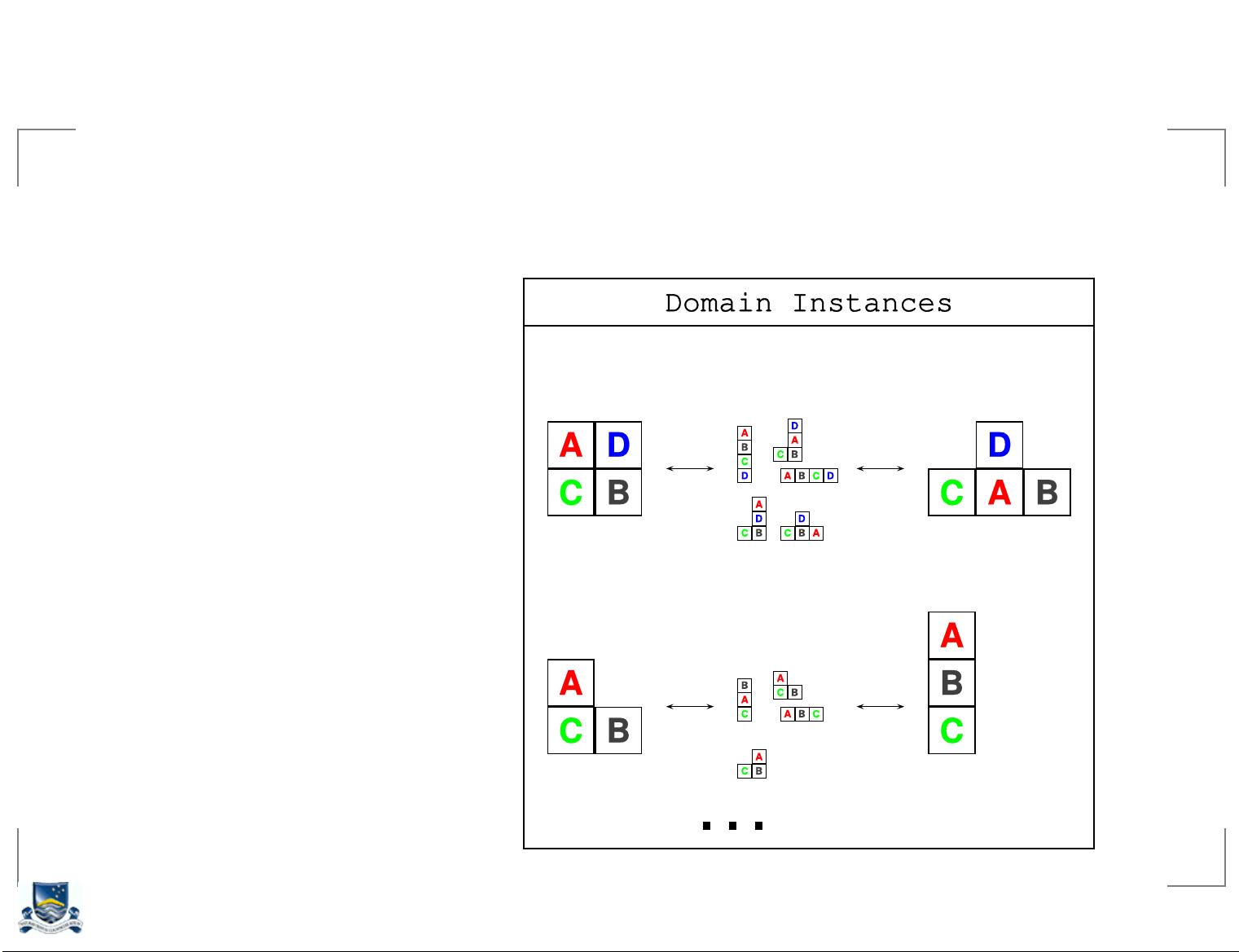 8. **规划（Planning in MDPs）**: MDPs常常与规划算法结合使用，如价值迭代、政策迭代或基于搜索的方法（如深度优先搜索、广度优先搜索）。规划旨在找到或学习一个最优策略，以解决给定的MDP实例。 **规划示例**: 给出的规划示例可能是一个简单的迷宫环境，其中有两个状态S和F，表示起点和终点，以及三个动作move(,), move(A,TAB), move(S,F)和move(F,S)。move(,)表示原地不动，而move(A,TAB)和move(S,F)分别对应向左和向右移动。在每个状态下，move(S,F)的概率较高（0.9），而move(F,S)的概率较低（0.1）。规划的任务是找到一个策略，使得从S出发，通过一系列决策最终到达F，同时最大化累积奖励。 MDPs广泛应用于强化学习、机器人控制、游戏AI等领域，为智能体在不确定环境中做出决策提供了一个理论基础。理解并应用MDPs的关键在于明确问题的结构，设计合理的奖励函数，并选择合适的算法来求解最优策略。