C++编程:中缀表达式转后缀表达式的栈实现
45 浏览量
更新于2024-09-01
收藏 232KB PDF 举报
"C++利用栈实现中缀表达式转后缀表达式"
中缀表达式是一种常见的数学表达式形式,其中运算符位于操作数之间,例如 `1 + 2 * 3`。后缀表达式,又称逆波兰表示法,是另一种表达方式,运算符放在操作数之后,如 `1 2 3 * +`。这种表示法在计算上更为方便,因为不需要考虑括号和运算符优先级。
转换中缀表达式为后缀表达式的关键在于使用栈来处理运算符。以下是一个详细的步骤解析:
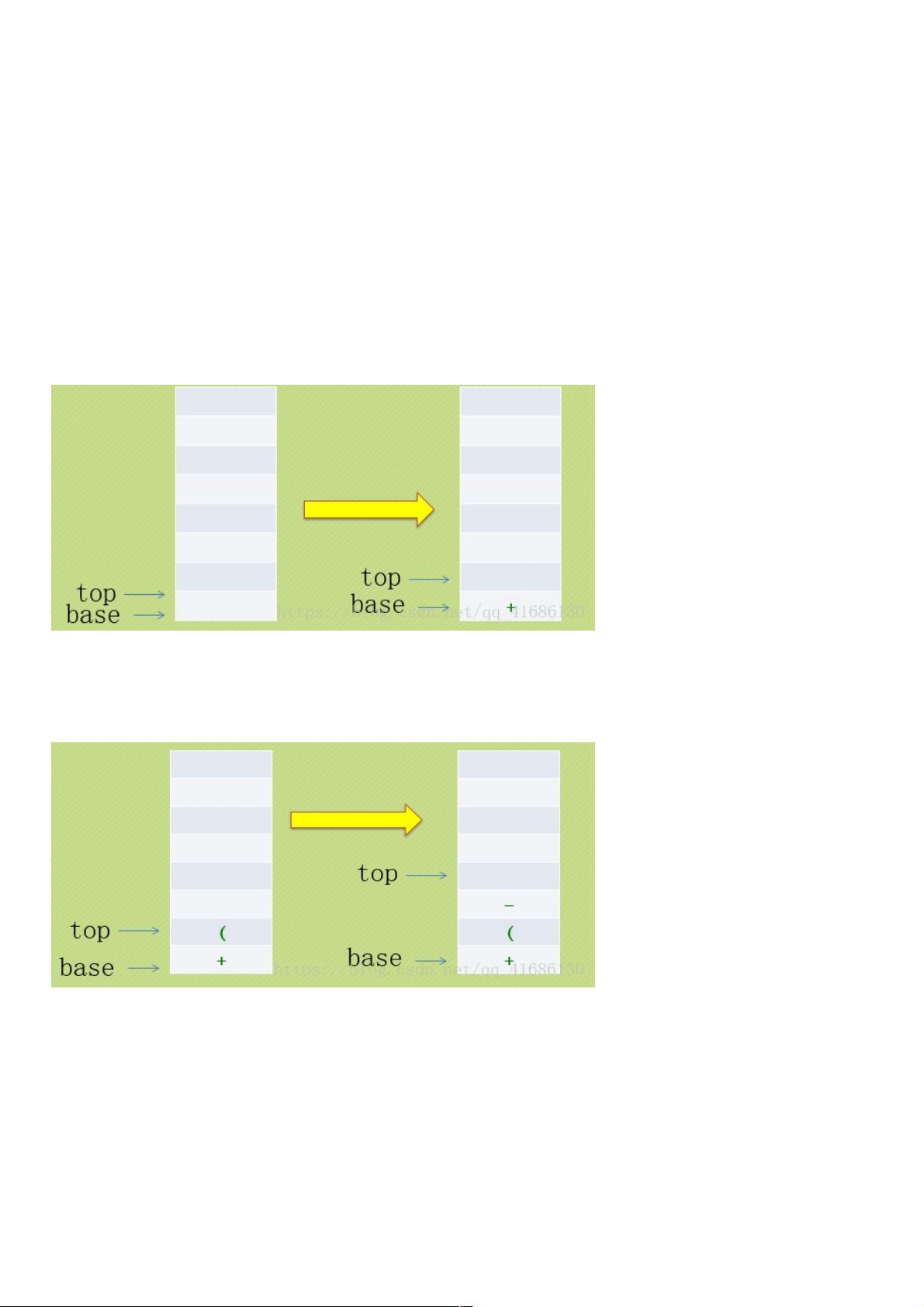
1. 初始化一个栈,通常用于存储运算符。
2. 从左到右逐个读取中缀表达式中的字符,如果是数字,直接输出到后缀表达式中;如果是运算符,则进行以下判断:
- 如果运算符是左括号 '(',将其压入栈中。
- 如果运算符是右括号 ')',则不断弹出栈顶运算符并输出,直到遇到左括号为止。
- 如果运算符的优先级高于栈顶运算符(或栈为空),将运算符压入栈中。
- 如果运算符的优先级低于或等于栈顶运算符,将栈顶运算符弹出并输出,重复此过程,直到当前运算符的优先级高于栈顶运算符,然后将当前运算符压入栈。
3. 当所有字符都被处理后,将栈中剩余的运算符依次弹出并输出,因为它们是未完成的操作。
运算符的优先级通常如下:
- 左括号 '(' 具有最低优先级,用于开始一个运算子组。
- 乘法 '*' 和除法 '/' 具有比加法 '+' 和减法 '-' 更高的优先级。
- 当遇到相同优先级的运算符时,遵循“先入后出”(LIFO,Last In First Out)原则,即后来的运算符先运算。
在C++中实现这个算法,通常会使用自定义栈结构,如文中示例所示,栈的元素类型可能是字符或者自定义的运算符结构体。栈的初始化、压栈、弹栈等操作都需要通过函数实现。在处理表达式时,还需要一个循环来遍历输入字符串,每次处理一个字符。
以下是一个简化的代码框架:
```cpp
#include <stack>
#include <string>
std::string infix_to_postfix(const std::string& infix_expr) {
std::stack<char> opStack;
std::string postfixExpr;
for (char c : infix_expr) {
if (isdigit(c)) { // 数字直接添加到后缀表达式
postfixExpr += c;
} else if (c == '(') { // 左括号入栈
opStack.push(c);
} else if (c == ')') { // 右括号,弹出栈顶运算符直至遇到左括号
while (!opStack.empty() && opStack.top() != '(') {
postfixExpr += opStack.top();
opStack.pop();
}
if (!opStack.empty()) {
opStack.pop(); // 弹出左括号
}
} else if (isoperator(c)) { // 运算符
while (!opStack.empty() && precedence(c) <= precedence(opStack.top())) {
postfixExpr += opStack.top();
opStack.pop();
}
opStack.push(c);
}
}
// 弹出栈中剩余的运算符
while (!opStack.empty()) {
postfixExpr += opStack.top();
opStack.pop();
}
return postfixExpr;
}
// 预定义的运算符优先级函数(此处省略实现)
int precedence(char op);
```
这段代码的核心逻辑与题目中的描述一致,但请注意,实际的代码实现需要包括对运算符优先级的处理以及错误检查,例如处理未匹配的括号。此外,`isoperator()` 和 `precedence()` 函数需要根据具体需求进行定义,以确定运算符的合法性及其优先级。
2023-05-30 上传
2023-12-18 上传
2023-07-25 上传
点击了解资源详情
weixin_38558659
- 粉丝: 6
- 资源: 917
最新资源
- SSM动力电池数据管理系统源码及数据库详解
- R语言桑基图绘制与SCI图输入文件代码分析
- Linux下Sakagari Hurricane翻译工作:cpktools的使用教程
- prettybench: 让 Go 基准测试结果更易读
- Python官方文档查询库,提升开发效率与时间节约
- 基于Django的Python就业系统毕设源码
- 高并发下的SpringBoot与Nginx+Redis会话共享解决方案
- 构建问答游戏:Node.js与Express.js实战教程
- MATLAB在旅行商问题中的应用与优化方法研究
- OMAPL138 DSP平台UPP接口编程实践
- 杰克逊维尔非营利地基工程的VMS项目介绍
- 宠物猫企业网站模板PHP源码下载
- 52简易计算器源码解析与下载指南
- 探索Node.js v6.2.1 - 事件驱动的高性能Web服务器环境
- 找回WinSCP密码的神器:winscppasswd工具介绍
- xctools:解析Xcode命令行工具输出的Ruby库