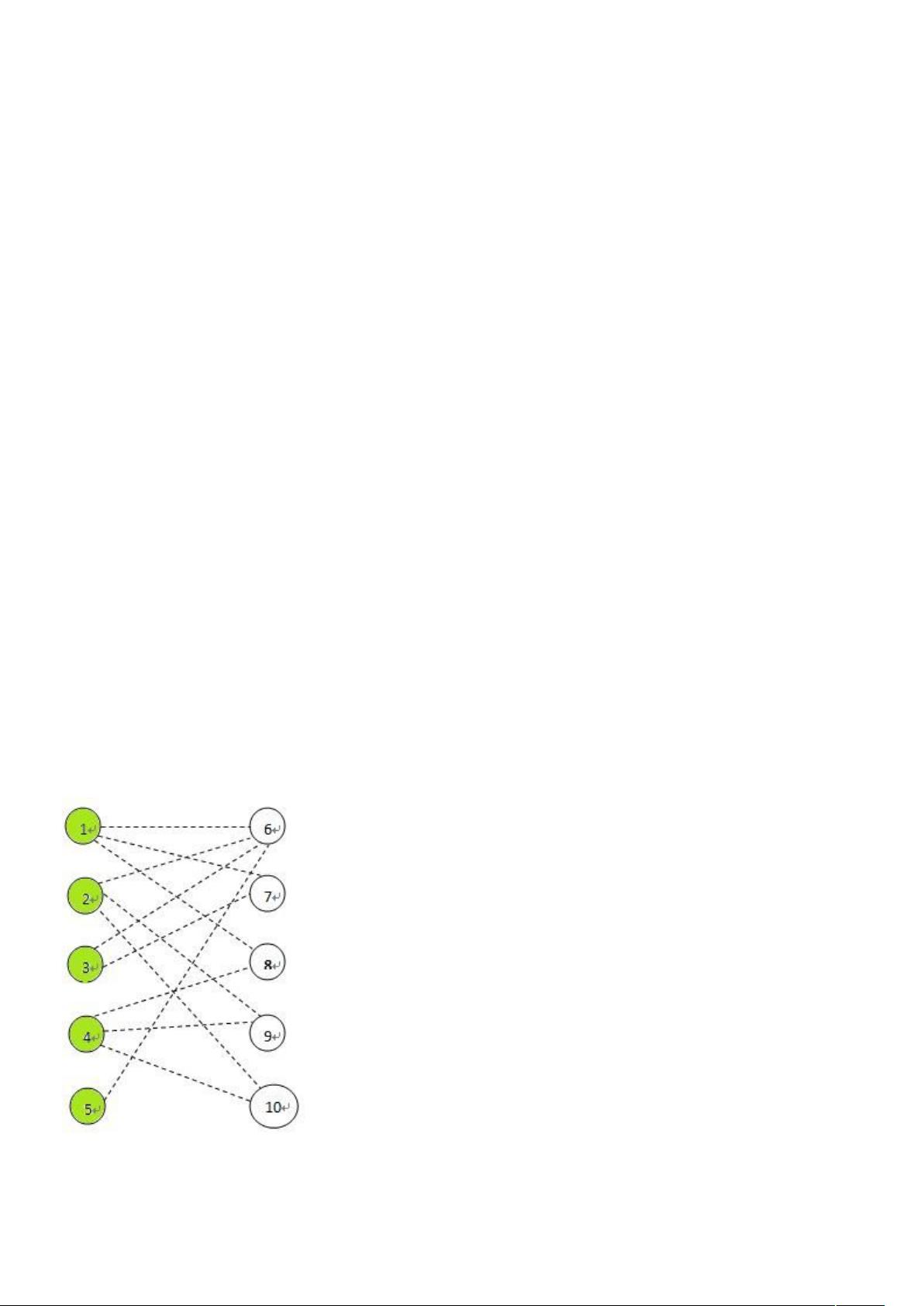
二分图匹配算法实现：DFS-Edmonds与Hopcroft-Karp

"二分图匹配的算法实现包括DFS-Edmonds、BFS-Edmonds和Hopcroft-Karp。二分图是一种特殊的无向图，其中的顶点可以被分割成两个互不相交的集合，所有边都连接不同集合内的顶点。二分图的匹配问题是寻找最大数量的边，使得每条边的两个顶点都不相同，即没有公共端点。最大匹配在图论中具有重要应用，例如在分配问题和网络流问题中。 1. 匹配和二分图的概念： 匹配是指在无向图中，一组边的集合，其中任意两条边没有共同的端点。最大匹配问题旨在找到尽可能多的匹配边，覆盖最多的顶点。二分图的匹配问题更易于处理，因为它们简化了问题的结构。 2. 二分图的性质： - 二分图的判定可以通过BFS进行，如果图能被染成两种颜色且所有路径的长度都是偶数，那么它就是二分图。 - Konig定理指出，在二分图中，顶点的度之和等于边的数。这与握手定理类似，意味着在一个无环图中，边的数量等于所有顶点的度之和的一半。 3. 匈牙利算法： 匈牙利算法，又称Kuhn-Munkres算法或KM算法，是一种求解二分图最大匹配的高效算法。它的核心思想是通过寻找增广路径来增加匹配的数量。在DFS和BFS版本中，算法会构建一个树状结构，通过递归的方式构造层次，并尝试找到未匹配的顶点，以增加匹配数。DFS适用于稠密图，而BFS适用于稀疏图，它们的时间复杂度均为O(n^3)。 4. Hopcroft-Karp算法： Hopcroft-Karp算法是另一种求解二分图最大匹配的方法，它利用了深度优先搜索和广度优先搜索的结合。算法首先寻找最短的增广路径，然后更新匹配。这种方法在稀疏图中效率更高，其时间复杂度为O(n^1.5)。 5. DFS-Edmonds和BFS-Edmonds算法： 这些是基于Edmonds算法的变体，同样用于解决二分图的最大匹配问题。DFS-Edmonds算法使用深度优先搜索策略，而BFS-Edmonds则采用广度优先搜索。它们也寻找增广路径，但具体的实现细节和优化可能有所不同。 在实际应用中，这些算法广泛用于解决实际问题，如任务调度、分配问题（如稳定婚姻问题）和网络路由等。理解并掌握这些算法对于解决复杂的图论问题至关重要。"