图灵机与递归可枚举语言解析

"形式语言与自动机：第十二讲 图灵机与递归可枚举语言" 本讲主要探讨了图灵机的概念及其在描述递归可枚举语言中的作用。图灵机是理论计算机科学的基础，它是一种抽象计算模型，用于模拟有限存储设备上的计算过程。图灵机由以下几个关键组成部分构成： 1. **有限状态控制**：包含一组状态，机器在执行过程中会从一个状态转移到另一个状态。 2. **带（Tape）**：无限长的单向分段介质，每个分段（单元格）可以存储一个符号。 3. **带头（Tapehead）**：可以读取当前单元格的符号，并根据需要改变这个符号或移动到下一个单元格。 4. **带符（Tapesymbols）**：带上的可写字符集。 5. **转移函数**：定义了当机器处于特定状态并读取特定符号时，如何更新状态、写入新符号以及移动带头的方向。 6. **开始状态（Start State）**：图灵机开始运行时的状态。 7. **空白符号（Blank Symbol）**：通常表示带上的空位。 8. **终态集合（Final States）**：图灵机达到这些状态时，表示计算完成。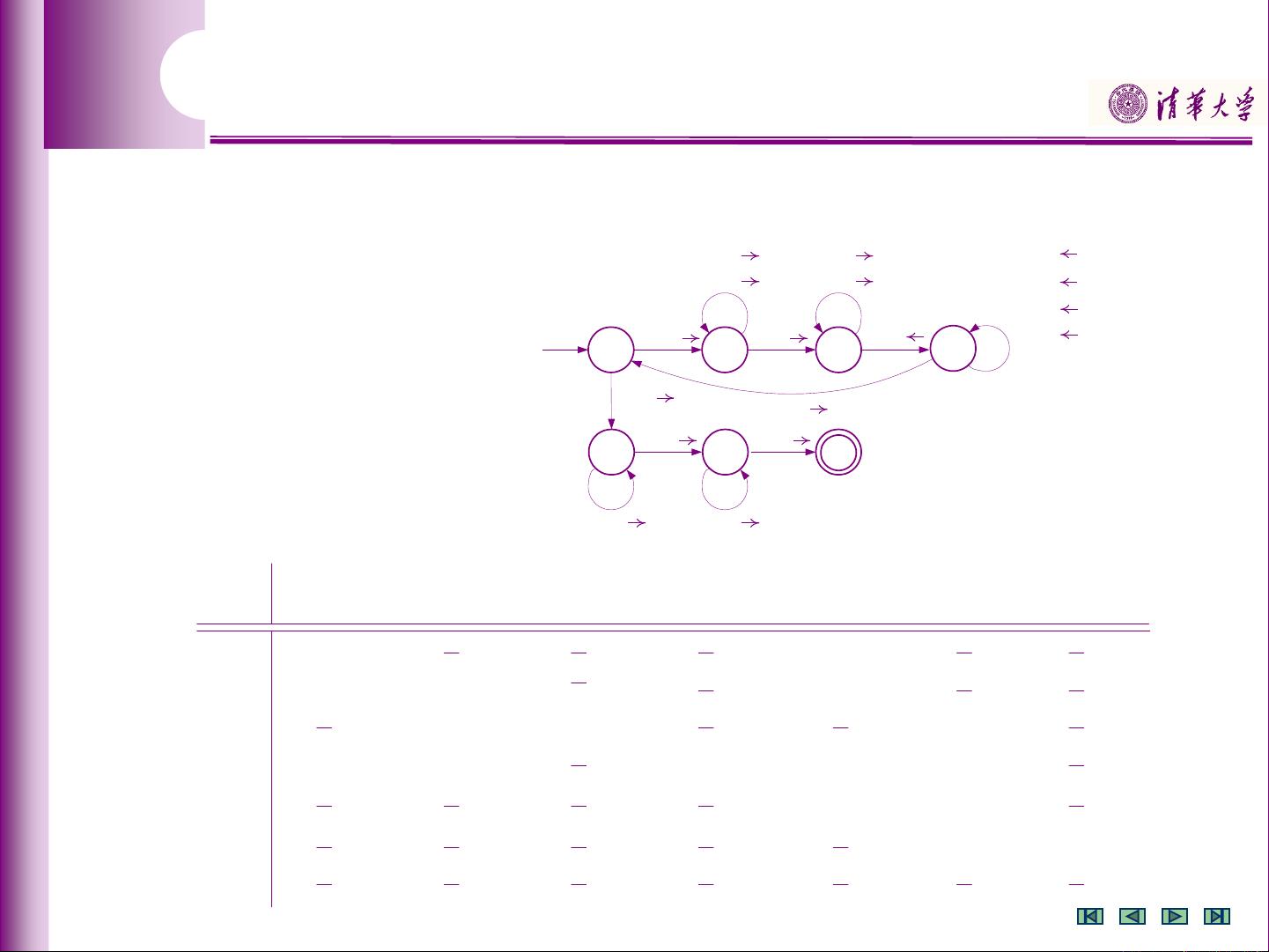 通过转移函数，图灵机可以模拟任何逻辑或算术过程，只要这些过程可以在有限步骤内完成。例如，给出的图灵机示例接受语言L={0^n1^n2^n|n≥1}，即由相同数量的0、1和2组成的字符串。 **递归可枚举语言（Recursively Enumerable Language, REL）**是指可以用图灵机识别但不一定能用图灵机决定的语言。如果一个语言L中的每个字符串都能被某个图灵机以有限的步骤接受，那么L就是递归可枚举的。然而，递归可枚举语言中可能存在某些字符串，没有图灵机能在有限步骤内确定它们是否属于该语言。 此外，**递归语言（Recursive Language）**是递归可枚举语言的一个子集，不仅可以用图灵机识别，而且可以用图灵机决定。也就是说，对于递归语言，存在一个图灵机，对于任何输入，它都能在有限步骤内确定该输入是否属于该语言。 **基本图灵机**是最简单的形式，通常有有限的输入和带符集，转移函数也是有限的。通过扩展基本图灵机，可以引入更复杂的结构，如多带图灵机、非确定性图灵机等。 **受限的图灵机**，如1/3-Turing机，是在某些方面限制了图灵机的能力，例如限制带头的移动速度或限制可用的带符数量。这样的限制可以用来研究计算能力的边界。 **图灵机与计算机**之间的关系在于，现代计算机的设计理念受到了图灵机的启发。尽管实际的计算机有内存限制，但它们在原理上可以被视为一个有限的、快速的、有错误处理功能的图灵机。 这一讲深入地探讨了图灵机作为计算模型的核心概念，以及它们在理解和分类可计算语言方面的应用。通过学习图灵机，我们可以更好地理解计算的界限以及计算机能够解决的问题类型。