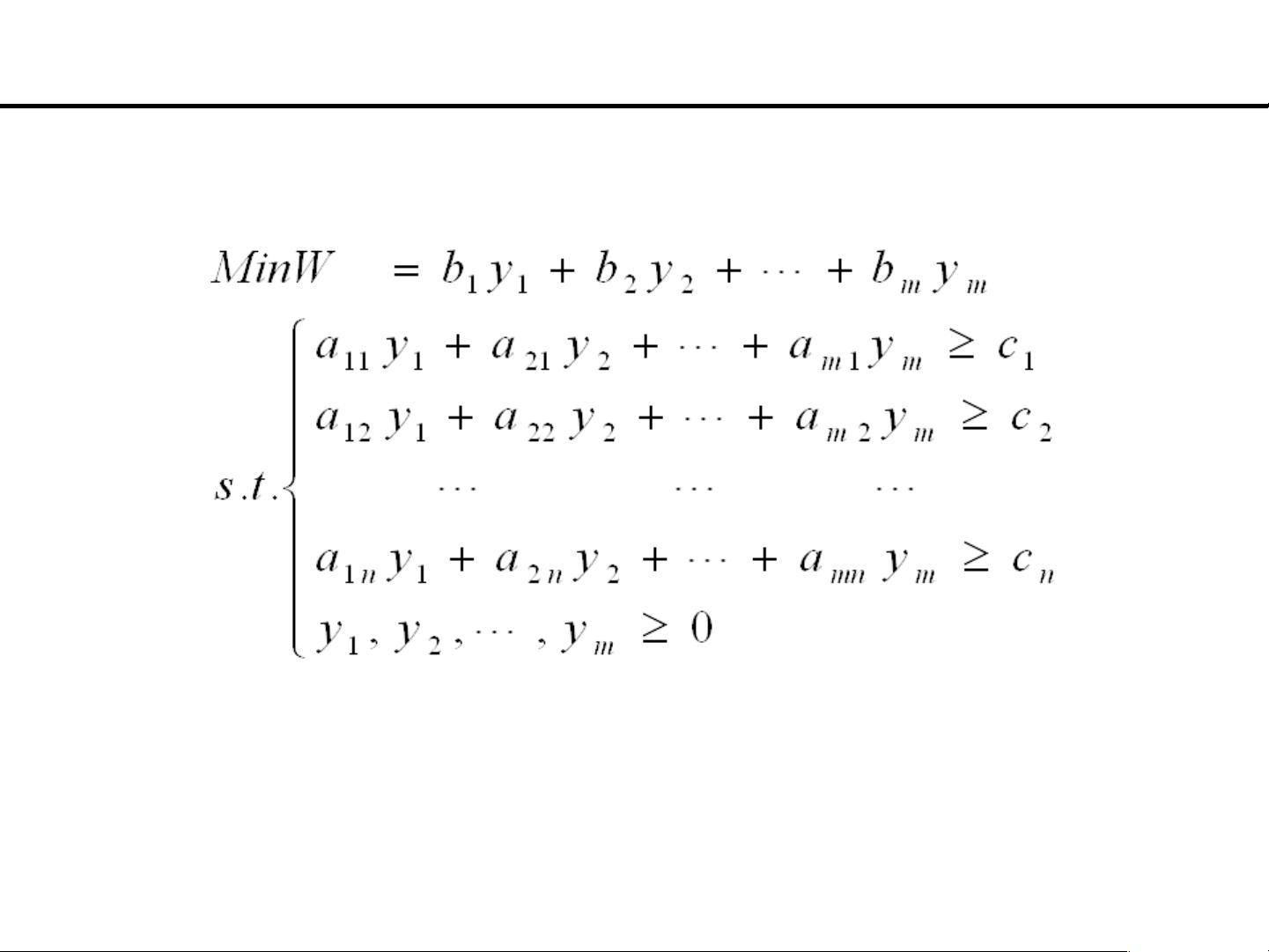线性规划对偶理论及其应用

线性规划的对偶理论 线性规划的对偶理论是运筹学中一个重要的概念，它研究的是对偶问题之间的关系及其解的性质。对偶理论的应用非常广泛，包括经济管理、生产计划、供应链管理等领域。 在线性规划中，对偶理论是指对任何一个求极大值的线性规划问题，都有一个求极小值的线性规划问题与之对应，反之亦然。其中一个为原问题，另一个就为对偶问题。对偶理论的研究就是研究对偶问题之间的关系及其解的性质。 对偶问题的一般概念可以通过一个简单的例子来说明。例如，周长一定的矩形中，以正方形面积最大；面积一定的矩形中，以正方形周长最小。这两个问题之间存在着对偶关系。对偶理论的应用可以帮助我们更好地理解和解决这类问题。 在经济管理中，对偶理论的应用是非常广泛的。例如，某工厂生产两种产品甲和乙，生产中需4种设备按A，B，C，D顺序加工，每件产品加工所需的机时数、每件产品的利润值及每种设备的可利用机时数可以列入表中。对偶问题的提出可以帮助工厂 अध्यापक充分利用设备机时，获得最大利润。 对偶理论的应用还可以帮助我们解决一些实际问题。例如，若厂长决定不生产甲和乙型产品，决定出租机器用于接受外加工，只收加工费，那么４种机器的机时如何定价才是最佳决策？对偶理论的应用可以帮助我们找到最佳决策。 在实际应用中，对偶理论的应用可以帮助我们解决一些复杂的问题。例如，采购甲、乙、丙、丁4种食品量分别为x1，x2，x3，x4，在保证人体所需维生素A、B、C前提下，使总的花费最小。对偶理论的应用可以帮助我们找到最佳的采购策略。 对偶理论是线性规划中一个非常重要的概念，它的应用非常广泛，可以帮助我们解决一些复杂的问题。但是，对偶理论的应用也需要我们具备一定的数学基础和计算机编程技能。 "线性规划的对偶理论"