卷积网络详解：概念、运算与深度学习应用

第九章主要探讨了卷积网络（Convolutional Neural Networks, CNNs）的基本概念和应用，它是专门针对具有网络结构数据如时间序列和图像数据设计的深度学习模型。卷积网络的核心在于其特有的卷积运算，这是一种在神经网络中替代传统矩阵乘法的计算方式。 卷积运算是数学上的一个重要概念，它涉及两个可积函数的交互作用，通过积分来形成新的函数。在卷积神经网络中，输入（input）通常是一个多维数组，如图像或信号，而核函数（kernel function）则是另一个多维数组，其参数通过学习算法优化。输出特征映射（feature map）是卷积结果，它反映了输入与核函数的特定卷积特性。 在机器学习的实现中，卷积运算通常针对输入数据的每个位置进行，并且可以同时在多个维度上进行，如一维、二维乃至更高维度。卷积运算具有交换性，即输入和核函数交换位置后不会改变结果，这是通过核的翻转（flipping）来确保的。实际上，许多神经网络库提供了互相关（cross-correlation）函数，它与卷积的区别在于不翻转核。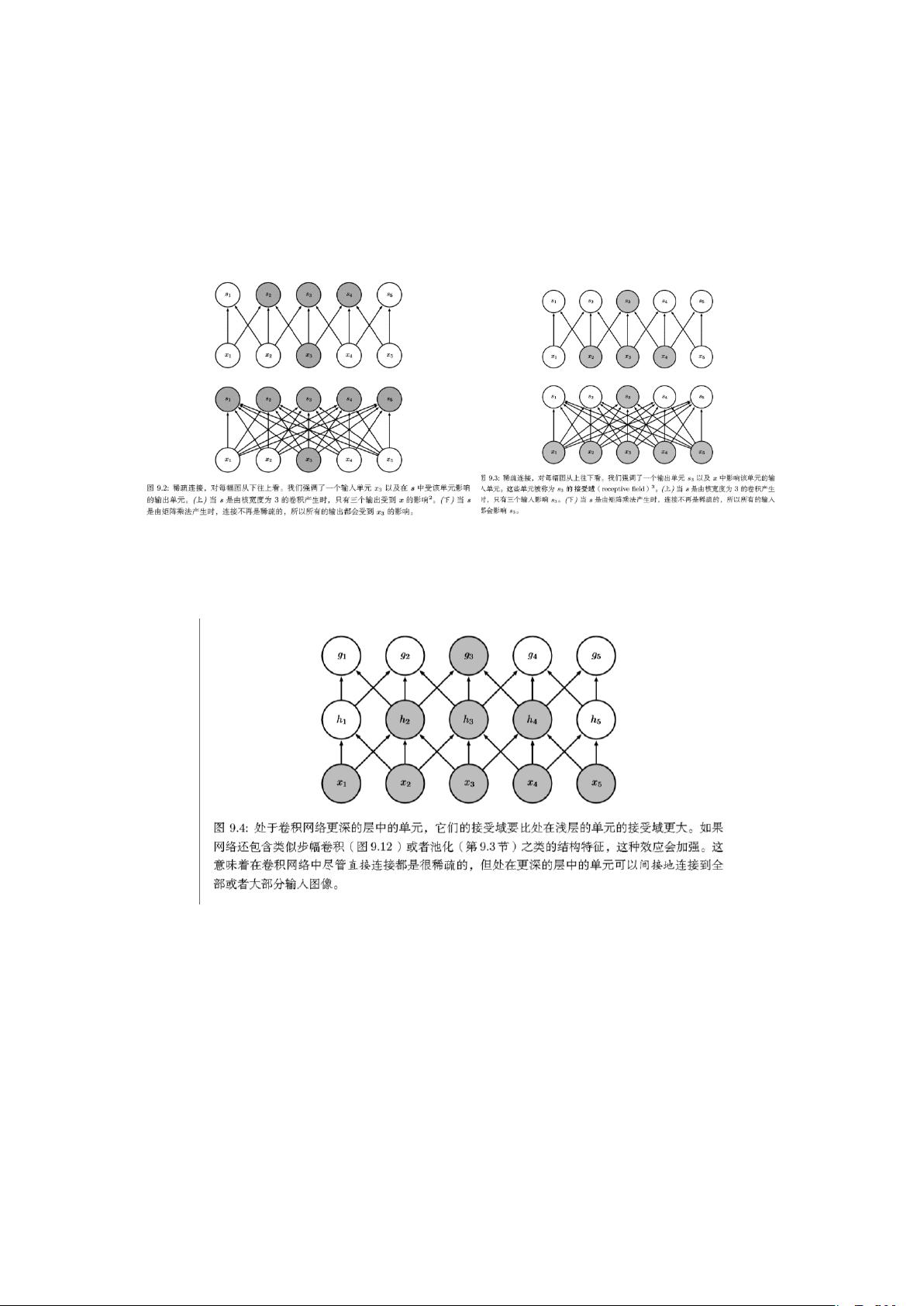 卷积操作可以看作是矩阵乘法的一种特殊情况，涉及到Toeplitz矩阵或双重分块循环矩阵，这些矩阵的特点是元素分布具有周期性和稀疏性。这意味着卷积操作不仅高效，而且能够捕捉输入数据中的局部特征，这是卷积网络在图像识别、语音处理等领域取得显著效果的关键。 在卷积网络的实际应用中，核的大小、步长和填充（padding）等因素会影响网络的性能。学习算法通过调整这些参数，使网络能够适应不同任务，如物体检测、分类或生成任务。卷积神经网络的结构设计使得它们在处理数据的平移不变性方面表现出色，这在很多视觉任务中是非常重要的。 第九章深入剖析了卷积网络的基础原理和优势，展示了如何利用卷积运算有效地处理具有网络结构的数据，这对于理解现代深度学习框架中的核心组件以及开发实际应用具有重要意义。