二维数组常见难题解析：分析问题，解决难题

# 1. 二维数组的基本概念**

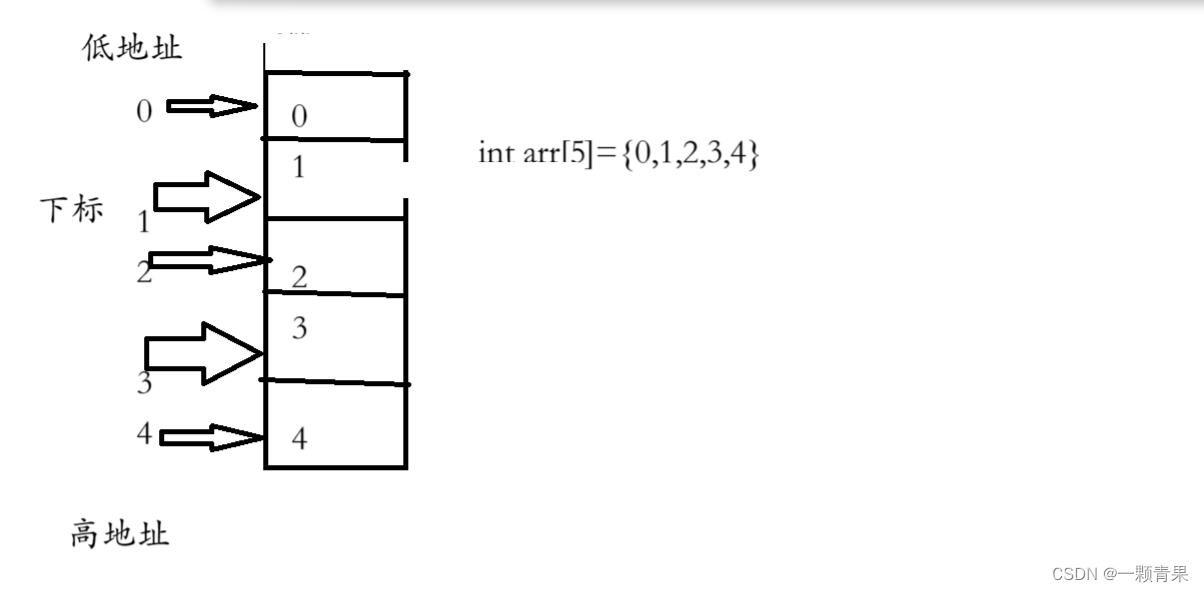
二维数组是一种数据结构，它可以存储具有两个索引的元素。它可以被视为一个由行和列组成的表格，其中每个元素都由其行和列索引唯一标识。

在 C++ 中，二维数组可以通过以下方式声明：

int arr[m][n];

其中，`m` 是行数，`n` 是列数。

二维数组中的元素可以通过以下方式访问：

arr[i][j]

其中，`i` 是行索引，`j` 是列索引。

# 2. 二维数组常见问题

### 2.1 数组越界问题

#### 2.1.1 越界原因分析

二维数组越界问题是指访问数组元素时，超出数组的有效范围。这通常是由以下原因引起的：

- **索引超出数组大小：**访问数组元素时，使用的索引超出数组的有效范围，例如访问一个不存在的元素。
- **数组未初始化：**在使用数组之前，未对其进行初始化，导致数组中包含垃圾值，访问这些值可能会导致越界。
- **数组指针操作不当：**在使用数组指针时，指针超出数组的有效范围，导致访问无效内存地址。

#### 2.1.2 越界解决方法

解决数组越界问题的方法包括：

- **边界检查：**在访问数组元素之前，检查索引是否在数组的有效范围内。
- **使用哨兵值：**在数组末尾添加一个哨兵值，以指示数组的结束。
- **动态分配数组：**使用动态分配的数组，可以根据需要调整数组的大小，避免越界问题。

### 2.2 数组元素访问问题

#### 2.2.1 元素访问方式

二维数组元素的访问方式有两种：

- **行优先访问：**按行遍历数组，先访问每一行的所有元素，再访问下一行。
- **列优先访问：**按列遍历数组，先访问每一列的所有元素，再访问下一列。

#### 2.2.2 元素访问异常处理

在访问数组元素时，可能会遇到以下异常：

- **数组索引越界异常：**访问超出数组有效范围的元素时，会引发此异常。
- **空指针异常：**访问未初始化的数组或数组指针时，会引发此异常。
- **段错误：**访问无效内存地址时，会引发此错误。

处理这些异常的方法包括：

- **边界检查：**在访问数组元素之前，检查索引是否在数组的有效范围内。
- **使用异常处理：**使用 try-catch 块捕获数组访问异常，并进行适当处理。
- **使用断言：**使用断言来检查数组的有效性，并及时发现越界问题。

# 边界检查示例
array = [[1, 2, 3], [4, 5, 6]]

try:
    # 访问超出数组有效范围的元素
    print(array[2][3])
except IndexError:
    print("数组越界！")

# 异常处理示例
try:
    # 访问未初始化的数组
    print(array[0][0])
except NameError:
    print("数组未初始化！")

# 断言示例
assert array[0][0] == 1, "数组元素访问错误！"

# 3. 二维数组常见算法

### 3.1 数组遍历算法

数组遍历算法是指对二维数组中的所有元素进行逐个访问和处理。常见的有两种遍历方式：行优先遍历和列优先遍历。

#### 3.1.1 行优先遍历

行优先遍历是指先遍历完第一行，再遍历第二行，依次遍历完所有行。

for (int i = 0; i < row; i++) {
    for (int j = 0; j < col; j++) {
        // 对第 i 行第 j 列的元素进行操作
    }
}

**代码逻辑分析：**

* 外层循环遍历行，从第 0 行到第 row-1 行。
* 内层循环遍历列，从第 0 列到第 col-1 列。
* 每次循环都会访问第 i 行第 j 列的元素。

#### 3.1.2 列优先遍历

列优先遍历是指先遍历完第一列，再遍历第二列，依次遍历完所有列。

for (int j = 0; j < col; j++) {
    for (int i = 0; i < row; i++) {
        // 对第 i 行第 j 列的元素进行操作
    }
}

**代码逻辑分析：**

* 外层循环遍历列，从第 0 列到第 col-1 列。
* 内层循环遍历行，从第 0 行到第 row-1 行。
* 每次循环都会访问第 i 行第 j 列的元素。

### 3.2 数组元素查找算法

数组元素查找算法是指在二维数组中查找特定元素的位置或存在性。常见的有顺序查找和二分查找。

#### 3.2.1 顺序查找

顺序查找是指从数组的第一个元素开始，逐个比较元素，直到找到目标元素或遍历完整个数组。

for (int i = 0; i < row; i++) {
    for (int j = 0; j < col; j+