算法竞赛中的二维数组：解决复杂问题，提升算法能力

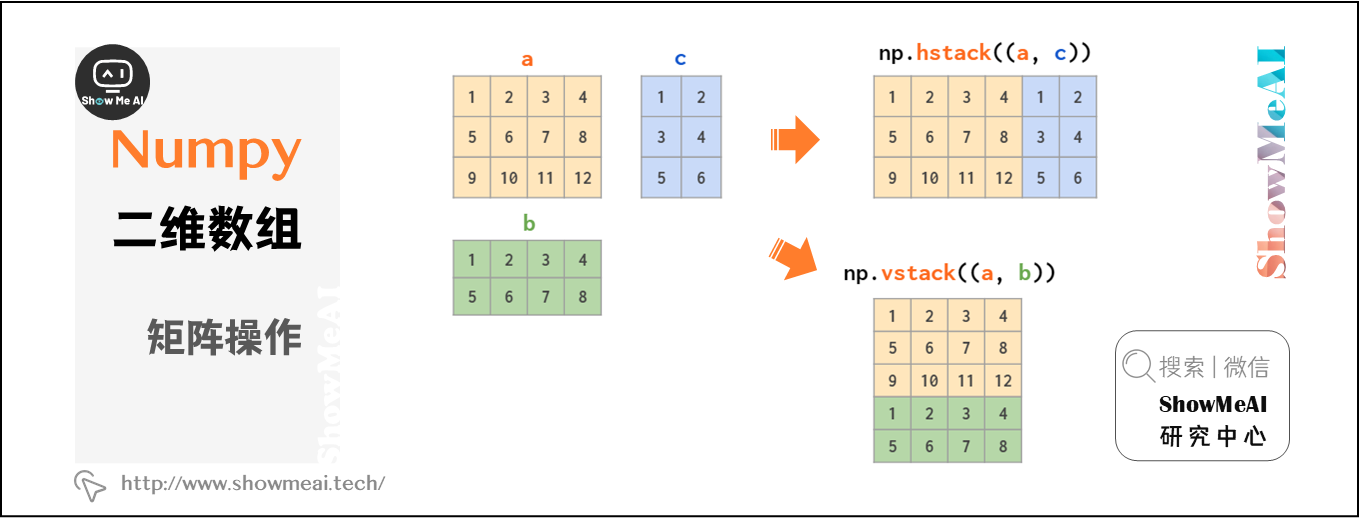
# 1. 二维数组基础

二维数组是一种数据结构，它由一系列行和列组成，每个单元格都存储一个值。与一维数组不同，二维数组允许您按行和列组织数据，从而提供更灵活和结构化的数据表示方式。

二维数组通常用于表示表格数据、图像或矩阵。例如，一个电子表格可以表示为一个二维数组，其中行代表记录，列代表字段。同样，一个图像可以表示为一个二维数组，其中每个单元格存储一个像素的颜色值。

二维数组可以使用嵌套循环进行访问。外层循环遍历行，内层循环遍历列。通过使用索引，您可以访问特定单元格中的值。例如，以下代码片段访问二维数组 `array` 中第二行第三列的元素：

array[1][2]

# 2. 二维数组的算法应用

二维数组在算法中的应用广泛，涉及查找、排序、动态规划等多个方面。本章节将介绍二维数组在算法中的典型应用，包括线性查找、二分查找、冒泡排序、快速排序、0-1背包问题和最长公共子序列问题。

### 2.1 查找算法

查找算法是算法中常用的基本操作，用于在数据结构中查找特定元素。二维数组中常用的查找算法包括线性查找和二分查找。

#### 2.1.1 线性查找

线性查找是一种简单的查找算法，从数组的第一个元素开始，依次比较每个元素是否与要查找的元素相等，直到找到目标元素或遍历完整个数组。

def linear_search(arr, target):
    for row in arr:
        for col in row:
            if col == target:
                return True
    return False

**代码逻辑逐行解读：**

* `for row in arr:`：遍历二维数组的每一行。
* `for col in row:`：遍历每一行的每一列。
* `if col == target:`：检查当前列元素是否等于目标元素。
* `return True`：如果找到目标元素，则返回 `True`。
* `return False`：如果遍历完整个数组都没有找到目标元素，则返回 `False`。

#### 2.1.2 二分查找

二分查找是一种更高效的查找算法，适用于有序数组。它通过不断将查找范围缩小一半，快速找到目标元素。

def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return True
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return False

**代码逻辑逐行解读：**

* `left, right = 0, len(arr) - 1`：初始化查找范围为数组的第一个元素和最后一个元素。
* `while left <= right:`：只要查找范围不为空，继续循环。
* `mid = (left + right) // 2`：计算查找范围的中点。
* `if arr[mid] == target:`：检查中点元素是否等于目标元素。
* `elif arr[mid] < target:`：如果中点元素小于目标元素，则将查找范围缩小到中点元素右侧。
* `else:`：如果中点元素大于目标元素，则将查找范围缩小到中点元素左侧。
* `return True`：如果找到目标元素，则返回 `True`。
* `return False`：如果遍历完整个查找范围都没有找到目标元素，则返回 `False`。

### 2.2 排序算法

排序算法用于将数据结构中的元素按特定顺序排列。二维数组中常用的排序算法包括冒泡排序和快速排序。

#### 2.2.1 冒泡排序

冒泡排序是一种简单的排序算法，通过不断比较相邻元素并交换顺序，将元素从小到大排序。

def bubble_sort(arr):
    for i in range(len(arr)):
        for j in range(len(arr[0])):
            for k in range(len(arr[0]) - 1):
                if arr[i][k] > arr[i][k + 1]:
                    arr[i][k], arr[i][k + 1] = arr[i][k + 1], arr[i][k]

**代码逻辑逐行解读：**

* `for i in range(len(arr)):`：遍历二维数组的每一行。
* `for j in range(len(arr[0])):`：遍历每一行的每一列。
* `for k in range(len(arr[0]) - 1):`：遍历每一行的相邻元素。
* `if arr[i][k] > arr[i][k + 1]:`：比较相邻元素的大小。
* `arr[i][k], arr[i][k + 1] = arr[i][k + 1], arr[i][k]`：如果相邻元素逆序，则交换顺序。

#### 2.2.2 快速排序

快速排序是一种高效的排序算法，通过分治法将数组划分为较小的子数组，然后递归地对子数组进行排序。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[0][0]
    left = []
    right = []
    for row in arr[1:]:
        for col in row:
            if col < pivot:
                left.append(col)
            else:
                right.append(col)
    return quick_sort(left) + [pivot] + quick_sort(right)

**