揭秘二维数组：掌握多维数据结构的奥秘

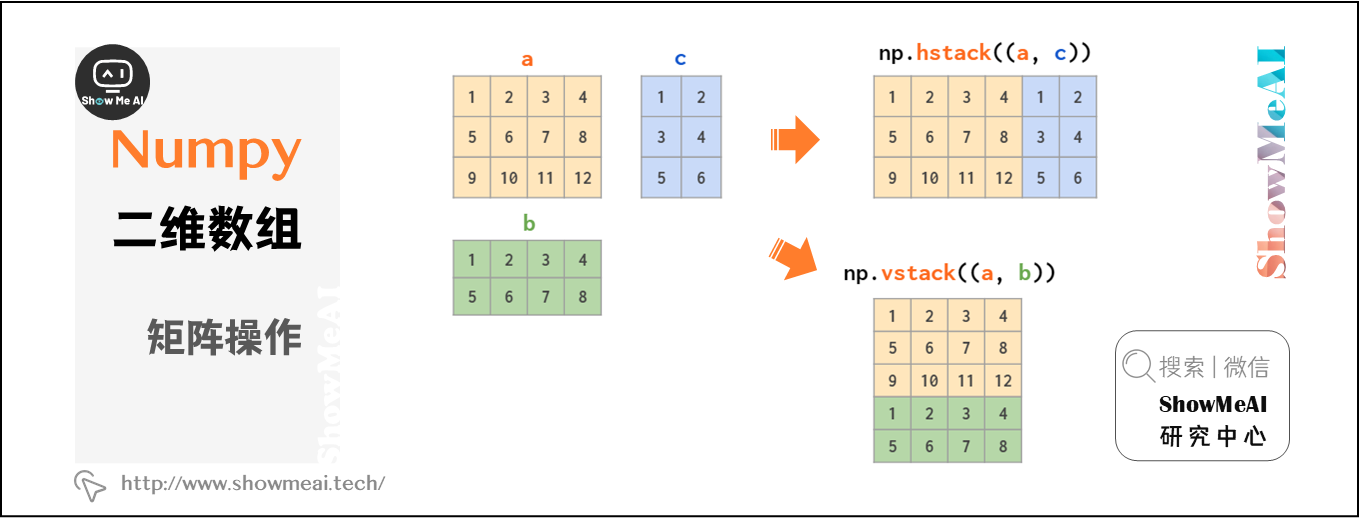
# 1. 二维数组的概念和基本操作**

二维数组是一种数据结构，它由行和列组成的矩形网格。每个元素都由一对索引标识，第一个索引表示行号，第二个索引表示列号。

**创建和初始化二维数组**

# 创建一个 3 行 4 列的二维数组
array = [[0] * 4 for _ in range(3)]

# 初始化二维数组
for i in range(3):
    for j in range(4):
        array[i][j] = i * 4 + j

**访问和修改元素**

# 访问元素
print(array[1][2])  # 输出 6

# 修改元素
array[1][2] = 10

# 2. 二维数组的遍历和搜索

二维数组是一种数据结构，它由行和列组成的元素集合组成。与一维数组不同，二维数组中的元素具有两个索引，分别表示行和列。这使得二维数组非常适合表示表格数据、图像和其他具有二维结构的数据。

### 2.1 顺序遍历

顺序遍历是遍历二维数组最简单的方法。它从左上角的元素开始，逐行逐列访问每个元素，直到到达右下角的元素。顺序遍历的伪代码如下：

for i in range(num_rows):
    for j in range(num_cols):
        # 访问元素 arr[i][j]

其中，`num_rows` 和 `num_cols` 分别表示二维数组的行数和列数。

**代码逻辑分析：**

* 外层循环 (`for i in range(num_rows)`) 遍历每一行。
* 内层循环 (`for j in range(num_cols)`) 遍历每一行的每一列。
* 在每个循环迭代中，都可以访问元素 `arr[i][j]”。

### 2.2 二分查找

二分查找是一种高效的搜索算法，用于在有序数组中查找特定元素。对于二维数组，我们可以将每一行视为一个有序数组，并对每一行应用二分查找。

**伪代码：**

def binary_search_2d(arr, target):
    for i in range(num_rows):
        low, high = 0, num_cols - 1
        while low <= high:
            mid = (low + high) // 2
            if arr[i][mid] == target:
                return i, mid
            elif arr[i][mid] < target:
                low = mid + 1
            else:
                high = mid - 1
    return -1, -1

其中，`target` 是要查找的元素。

**代码逻辑分析：**

* 外层循环 (`for i in range(num_rows)`) 遍历每一行。
* 内层循环 (`while low <= high`) 执行二分查找，直到找到目标元素或搜索范围为空。
* 在二分查找过程中，计算中间索引 `mid` 并将 `arr[i][mid]` 与 `target` 进行比较。
* 根据比较结果，更新 `low` 或 `high` 以缩小搜索范围。
* 如果找到目标元素，返回其行和列索引；否则，返回 `-1, -1`。

### 2.3 哈希查找

哈希查找是一种基于哈希表的快速搜索算法。对于二维数组，我们可以将每一行视为一个哈希表，并对每一行应用哈希查找。

**伪代码：**

def hash_search_2d(arr, target):
    for i in range(num_rows):
        hash_table = {}
        for j in range(num_cols):
            hash_table[arr[i][j]] = True
        if target in hash_table:
            return i, j
    return -1, -1

其中，`target` 是要查找的元素。

**代码逻辑分析：**

* 外层循环 (`for i in range(num_rows)`) 遍历每一行。
* 内层循环 (`for j in range(num_cols)`) 将每一行的元素插入哈希表中。
* 检查 `target` 是否存在于哈希表中。
* 如果找到目标元素，返回其行和列索引；否则，返回 `-1, -1`。

# 3.1 冒泡排序

冒泡排序是一种简单的排序算法，它通过不断比较相邻元素并交换位置，将最大元素逐个移动到数组末尾。

**算法流程：**

1. 初始化两个循环变量 `i` 和 `j`，其中 `i` 表示当前正在比较的元素，`j` 表示 `i` 左侧的元素。
2. 从 `i = 0` 开始，遍历数组。
3. 对于每个 `i`，从 `j = i + 1` 开始，遍历 `i` 右侧的元素。
4. 比较 `arr[i]` 和 `arr[j]`，如果 `arr[i] > arr[j]`，则交换这两个元素。
5. 重复步骤 2-4，直到 `i` 遍历完整个数组。

**代码实现：**

def bubble_sort(arr):
    """
    冒泡排序算法

    参数：
        arr: 待排序的二维数组

    返回：
        排序后的二维数组
    """

    for i in range(len(arr)):
        for j in range(i + 1, len(arr)):
            if arr[i] > arr[j]:
                arr[i], arr[j] = arr[j], arr[i]

    return arr

**逻辑分析：**

* 外层循环 `for i in range(len(arr))` 遍历数组每一行。
* 内层循环 `for j in range(i + 1, len(arr))` 遍历当前行右侧的元素。
* 如果 `arr[i]` 大于 `arr[j]`，则交换这两个元素，将 `arr[i]` 移动到右侧。
* 重复上述步骤，直到所有元素都比较完毕。

### 3.2 快速排序

快速排序是一种分治算法，它通过选择一个枢纽元素，将数组划分为两个子数组，然后递归地对子数组进行排序。

**算法流程：**

1. 选择一个枢纽元素 `pivot`。
2. 将数组划分为两个子数组：`left` 和 `right`，其中 `left` 包含所有小于 `pivot` 的元素，`right` 包含所有大于 `pivot` 的元素。
3. 递归地对 `left` 和 `right` 子数组进行排序。

**代码实现：**

def quick_sort(arr):
    """
    快速排序算法

    参数：
        arr: 待排序的二维数组

    返回：
        排序后的二维数组
    """

    def partition(arr, low, high):
        """
        分区函数

        参数：
            arr: 待排序的二维数组
            low: 分区开始索引
            high: 分区结束索引

        返回：
            枢纽元素在排序后的位置
        """

        pivot = arr[high]
        i = low - 1

        for j in range(low, high):
            if arr[j] <= pivot:
                i += 1
                arr[i], arr[j] = arr[j], arr[i]

        arr[i + 1], arr[high] = arr[high], arr[i + 1]

        return i + 1

    def sort(arr, low, high):
        """
        递归排序函数

        参数：
            arr: 待排序的二维数组
            low: 排序开始索引
            high: 排序结束索引
        """

        if low < high:
            pivot = partition(arr, low, high)
            sort(arr, low, pivot - 1)
            sort(arr, pivot + 1, high)

    sort(arr, 0, len(arr) - 1)

    return arr

**逻辑分析：**

* `partition` 函数选择最后一个元素作为枢纽元素，将数组划分为两个子数组。
* `sort` 函数递归地对子数组进行排序。
* 递归结束条件是 `low >= high`，表示子数组只有一个元素或为空。

### 3.3 筛选指定元素

筛选指定元素是指在二维数组中找到所有满足特定条件的元素。

**算法流程：**

1. 遍历数组每一行。
2. 对于每一行，遍历每一列。
3. 如果当前元素满足条件，则将其添加到结果列表中。

**代码实现：**

def filter_elements(arr, target):
    """
    筛选指定元素

    参数：
        arr: 待筛选的二维数组
        target: 目标元素

    返回：
        满足条件的元素列表
    """

    result = []

    for row in arr:
        for element in row:
            if element == target:
                result.append(element)

    return result

**逻辑分析：**

* 外层循环 `for row in arr` 遍历数组每一行。
* 内层循环 `for element in row` 遍历当前行每一列。
* 如果当前元素等于 `target`，则将其添加到结果列表中。

# 4. 二维数组的应用

二维数组在实际应用中有着广泛的用途，以下列举几个常见的应用场景：

### 4.1 图像处理

图像可以表示为二维数组，其中每个元素代表一个像素。通过对二维数组进行操作，可以实现图像的各种处理功能，例如：

- **图像灰度化：**将彩色图像转换为灰度图像，即将每个像素的 RGB 值转换为灰度值。
- **图像锐化：**增强图像的边缘和细节，通过使用卷积核对图像进行卷积运算。
- **图像模糊：**平滑图像，通过使用平均值或高斯滤波器对图像进行卷积运算。

import numpy as np
import cv2

# 读取图像
image = cv2.imread('image.jpg')

# 转换为灰度图像
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 显示图像
cv2.imshow('Original Image', image)
cv2.imshow('Grayscale Image', gray_image)
cv2.waitKey(0)
cv2.destroyAllWindows()

### 4.2 表格数据处理

二维数组可以用来存储表格数据，每一行代表一条记录，每一列代表一个字段。通过对二维数组进行操作，可以实现表格数据的各种处理功能，例如：

- **数据筛选：**根据指定的条件筛选出满足条件的数据。
- **数据排序：**根据指定的字段对数据进行排序。
- **数据聚合：**对数据进行聚合运算，例如求和、求平均值、求最大值等。

import pandas as pd

# 创建二维数组
data = [['John', 'Doe', 30], ['Jane', 'Smith', 25], ['Peter', 'Parker', 28]]

# 创建 DataFrame
df = pd.DataFrame(data, columns=['First Name', 'Last Name', 'Age'])

# 筛选年龄大于 25 的数据
filtered_df = df[df['Age'] > 25]

# 打印筛选后的数据
print(filtered_df)

### 4.3 游戏开发

二维数组在游戏开发中也扮演着重要的角色，例如：

- **游戏地图：**游戏地图可以表示为二维数组，其中每个元素代表一个地图单元格。
- **角色位置：**角色的位置可以用二维数组中的坐标表示。
- **路径查找：**通过对二维数组进行搜索，可以找到角色从一个位置移动到另一个位置的最短路径。

import pygame

# 创建游戏地图
map = [['#', '#', '#', '#', '#'],
       ['#', '.', '.', '.', '#'],
       ['#', '.', '.', '.', '#'],
       ['#', '.', '.', '.', '#'],
       ['#', '#', '#', '#', '#']]

# 创建角色
player = pygame.sprite.Sprite()
player.rect = pygame.Rect(1, 1, 32, 32)

# 移动角色
while True:
    # 处理事件
    for event in pygame.event.get():
        if event.type == pygame.KEYDOWN:
            if event.key == pygame.K_UP:
                player.rect.y -= 32
            elif event.key == pygame.K_DOWN:
                player.rect.y += 32
            elif event.key == pygame.K_LEFT:
                player.rect.x -= 32
            elif event.key == pygame.K_RIGHT:
                player.rect.x += 32

    # 渲染地图和角色
    screen.fill((0, 0, 0))
    for row in range(len(map)):
        for col in range(len(map[0])):
            if map[row][col] == '#':
                pygame.draw.rect(screen, (255, 255, 255), (col * 32, row * 32, 32, 32))
    screen.blit(player.image, player.rect)

    # 更新显示
    pygame.display.update()

# 5. 二维数组的优化

### 5.1 稀疏矩阵的表示和操作

#### 稀疏矩阵的概念

稀疏矩阵是指元素中大部分为零的矩阵。对于二维数组来说，稀疏矩阵的存储效率较低，因为大多数元素都是无意义的。为了优化稀疏矩阵的存储和操作，可以采用稀疏矩阵的表示方式。

#### 稀疏矩阵的表示

常用的稀疏矩阵表示方式有两种：

- **三元组表示法**：使用三个数组来存储稀疏矩阵，分别是行索引数组、列索引数组和值数组。其中，行索引数组和列索引数组分别存储非零元素所在的行和列，值数组存储非零元素的值。
- **压缩行存储（CSR）**：使用三个数组来存储稀疏矩阵，分别是值数组、行指针数组和列索引数组。其中，值数组存储非零元素的值，行指针数组存储每行的非零元素在值数组中的起始位置，列索引数组存储非零元素所在的列。

#### 稀疏矩阵的操作

对于稀疏矩阵，常见的操作包括：

- **转置**：将稀疏矩阵的行和列交换。
- **加法**：将两个稀疏矩阵相加，得到一个新的稀疏矩阵。
- **乘法**：将一个稀疏矩阵与一个稠密矩阵相乘，得到一个新的稠密矩阵。

### 5.2 数组的预分配

#### 预分配的概念

预分配是指在创建数组时，提前指定数组的大小。这可以避免数组在运行时自动扩容，从而提高程序的性能。

#### 预分配的优点

预分配的优点包括：

- **提高性能**：避免数组自动扩容的开销，提高程序运行效率。
- **减少内存碎片**：预分配可以确保数组在内存中连续分配，减少内存碎片。
- **避免内存错误**：如果数组未预分配，可能会在运行时出现内存错误。

#### 预分配的方式

在 Python 中，可以使用 `numpy.empty()` 或 `numpy.zeros()` 函数来预分配数组。例如：

import numpy as np

# 预分配一个 1000x1000 的数组
arr = np.empty((1000, 1000))

### 5.3 内存管理技巧

#### 内存泄漏

内存泄漏是指程序不再使用某块内存，但该内存仍然被程序占用，无法被释放的情况。内存泄漏会导致程序性能下降，甚至崩溃。

#### 内存管理技巧

为了避免内存泄漏，可以采用以下内存管理技巧：

- **使用引用计数**：Python 使用引用计数机制来管理内存。当一个对象不再被任何变量引用时，其引用计数为 0，会被自动释放。
- **使用垃圾回收**：Python 具有垃圾回收机制，会定期释放不再被引用的对象。
- **手动释放内存**：对于某些大型对象，可以手动释放其内存，以避免内存泄漏。可以使用 `del` 关键字来释放对象的内存。

# 6.1 多维数组

二维数组是一种存储在连续内存空间中的元素集合，它由行和列组成。多维数组是二维数组的扩展，它允许在二维数组的基础上增加额外的维度，形成三维、四维甚至更高维度的数组。

多维数组的声明与二维数组类似，只不过需要指定额外的维度大小。例如，声明一个三维数组：

array = numpy.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])

在这个例子中，`array`是一个三维数组，具有两个行维度和三个列维度。

### 多维数组的访问

访问多维数组中的元素与访问二维数组类似，只不过需要指定额外的索引。例如，要访问三维数组`array`中的元素`(1, 1, 2)`，可以使用以下语法：

element = array[1, 1, 2]

### 多维数组的遍历

遍历多维数组可以使用嵌套循环。例如，要遍历三维数组`array`中的所有元素，可以使用以下代码：

for i in range(array.shape[0]):
    for j in range(array.shape[1]):
        for k in range(array.shape[2]):
            element = array[i, j, k]

### 多维数组的应用

多维数组广泛应用于各种领域，包括：

- **图像处理：**存储图像数据，其中每个元素表示图像中的一个像素。
- **科学计算：**存储多维数据，例如模拟结果或实验数据。
- **机器学习：**存储训练数据或模型参数。