p值与假设检验：从入门到精通

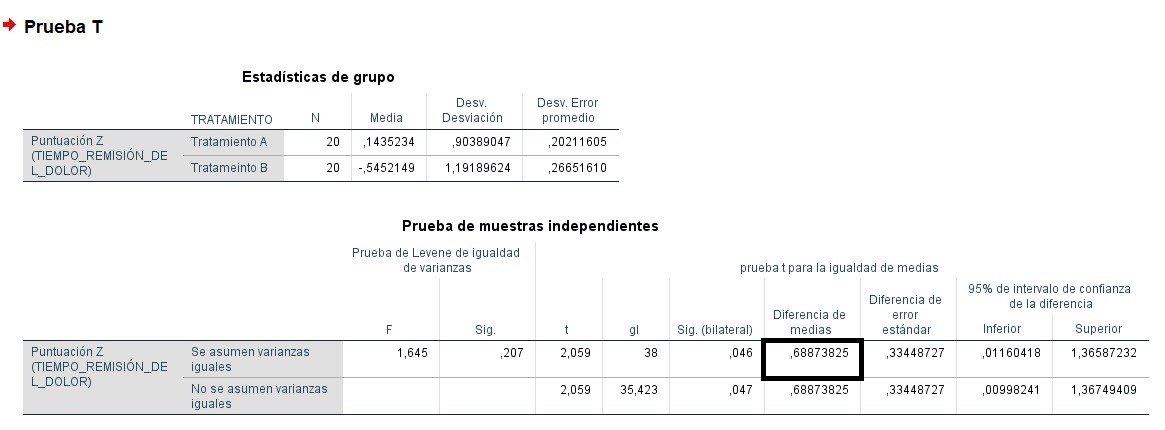
# 1. 统计学与假设检验简介

统计学是数据科学的核心，它为我们提供了一套理论和方法来处理不确定性，并从数据中提取有价值的信息。本章节中，我们首先将回顾统计学的基础知识，然后深入探讨假设检验的基本概念。假设检验是统计学中用于推断总体参数的一种重要方法，其核心在于通过样本数据来验证关于总体的假设是否成立。为了更直观地理解假设检验，我们将介绍它的基础理论和实际操作步骤。这不仅为接下来的p值的讨论奠定基础，也将帮助读者运用统计学原理在实际问题中做出科学的决策。

# 2. 理解p值的基本概念

p值作为统计推断中不可或缺的一部分，在统计检验中起到了至关重要的作用。理解p值，对于进行有效的假设检验至关重要。本章节将深入探讨p值的定义、计算方法以及它在假设检验中的关键角色。

## 2.1 p值的定义与解释
### 2.1.1 p值在统计推断中的角色
在统计学中，p值是用来衡量证据强度的指标，用于检验统计假设。在进行假设检验时，通常会设定一个零假设（通常表示为没有任何效应）和一个备择假设（表示为存在某种效应）。p值是在零假设为真的条件下，观察到当前结果或更极端结果出现的概率。如果这个概率很低，我们就有理由拒绝零假设，认为实验数据与零假设不一致。

p值在统计推断中的角色可以用以下三个主要方面来概括：

1. **决策依据**：p值常常作为接受或拒绝零假设的依据。传统上，如果p值小于预先设定的显著性水平（通常是0.05），则拒绝零假设。
2. **证据强度的度量**：p值也可以被看作是反对零假设的证据强度的度量。小的p值意味着观察到的数据不太可能在零假设为真的情况下发生。
3. **解释灵活性**：虽然p值提供了一个客观的检验统计假设的工具，但它并不提供效应大小或结果的实际重要性的信息。

### 2.1.2 如何理解p值的大小
理解p值的大小对于正确解释统计结果至关重要。以下是几个主要的思考角度：

1. **显著性水平（Alpha）**：在进行假设检验之前，研究者通常会设定一个显著性水平（如0.05或0.01）。p值如果小于显著性水平，意味着拒绝零假设，得到的结果在统计上是显著的。
2. **概率解释**：p值表示的是，在零假设为真的条件下，观察到当前结果或更极端结果的概率。p值越小，观察到的结果在零假设为真的情况下出现的可能性就越低。
3. **大小感**：虽然没有绝对的界限，但一般认为p值低于0.05为统计显著，而0.05到0.10之间的p值则被认为是边缘显著。不过，这不应成为硬性规则，因为p值只能说明证据的强度，而不是研究结果的重要性。

## 2.2 p值与假设检验的关系
### 2.2.1 假设检验的基本流程
假设检验是统计推断中的一个基本方法，用于决定一个样本数据是否支持某个统计假设。基本流程如下：

1. **定义假设**：首先明确定义零假设（H0）和备择假设（H1）。零假设通常表示没有效应或没有差异，而备择假设表示存在某种效应或差异。
2. **选择统计检验**：根据数据类型和研究设计选择合适的统计检验方法，如t检验、卡方检验等。
3. **计算检验统计量**：利用公式或软件计算出检验统计量的值。
4. **计算p值**：通过分布表或统计软件计算出该统计量对应的p值。
5. **做出决策**：根据p值与显著性水平的比较结果，决定是否拒绝零假设。

### 2.2.2 p值与拒绝域的概念
在假设检验中，拒绝域是指在零假设为真的条件下，导致检验统计量落在该区域的概率非常小的一组值。如果统计量落在拒绝域内，我们就拒绝零假设。

p值与拒绝域紧密相关。事实上，p值就是统计量落在拒绝域内的概率。如果p值小于显著性水平，我们就可以说统计量落在了拒绝域内，因此拒绝零假设。这个过程可以用下面的图示进行可视化：

graph LR
    A[开始] --> B[定义假设]
    B --> C[选择统计检验方法]
    C --> D[计算检验统计量]
    D --> E[计算p值]
    E --> F{p值与显著性水平比较}
    F -->|p < 显著性水平| G[拒绝零假设]
    F -->|p ≥ 显著性水平| H[不拒绝零假设]
    G --> I[结束]
    H --> I

## 2.3 p值的计算方法
p值的计算方法依赖于所进行的统计检验类型。以下，我们将介绍在连续型随机变量和离散型随机变量下p值的计算方法。

### 2.3.1 连续型随机变量下的p值计算
对于连续型随机变量，如正态分布，p值可以通过统计量和相应的概率密度函数来计算。例如，在进行单样本t检验时，可以通过以下步骤来计算p值：

1. 计算t统计量：t = (样本均值 - 总体均值) / (标准误差)
2. 根据自由度（n-1）和t统计量的值查找t分布表，找到相应的p值。
3. 或者使用统计软件直接计算p值。

### 2.3.2 离散型随机变量下的p值计算
对于离散型随机变量，如二项分布，计算p值稍微复杂。以二项检验为例，我们需要确定在零假设为真的情况下，观察到当前结果或更极端结果的概率。这需要使用概率质量函数（PMF）来计算。基本步骤如下：

1. 确定检验的二项分布参数：试验次数（n）和成功概率（p）。
2. 计算在零假设为真的条件下观察到当前结果的概率。
3. 如果是单尾检验，计算单边p值；如果是双尾检验，计算双边p值。
4. 使用适当的软件或手动计算来完成。

为了更直观地理解连续型随机变量和离散型随机变量下的p值计算，我们可以用以下的表格来总结这两种情况下计算的关键步骤：

| 类型 | 关键步骤 | 公式 | 说明 |
| --- | --- | --- | --- |
| 连续型 | 计算t统计量 | t = (样本均值 - 总体均值) / (标准误差) | 反映样本均值与总体均值的差异程度 |
| 连续型 | 查找t分布表 | p值 = P(T > t统计量) | 基于自由度和t统计量计算p值 |
| 离散型 | 确定参数 | n = 试验次数, p = 成功概率 | 参数用于计算PMF |
| 离散型 | 计算概率 | p值 = Σ P(X = x) | 概率反映了观察到当前结果或更极端结果的概率 |

以上表格展示了在不同随机变量类型下p值计算的关键步骤和公式。每一步的计算需要借助统计学的知识和工具来完成。

在下一章，我们将探讨p值的实际应用，包括在科学研究中的案例分析和数据分析软件中的实现方法。

# 3. p值的实际应用

在科学研究和数据分析中，p值扮演着至关重要的角色。这一章节将深入探讨p值在实际应用中的诸多方面，包括在科学研究中的应用、数据分析软件中如何实现对p值的计算，以及如何在实际工作中准确地表述和使用p值。

## 3.1 p值在科学研究中的应用

### 3.1.1 科学实验假设检验案例分析

在科学研究中，假设检验是一个关键步骤，它涉及到从实验数据中得出结论的过程。这里，我们通过一个简单的案例来分析p值如何在假设检验中发挥作用。

假设我们正在研究一种新药物对抗某种疾病的效力。在实验中，我们对比药物组和对照组之间的差异，以判断新药物是否有效。实验结果表明，药物组有显著的疗效提升。此时，我们就需要通过假设检验来确定这个结果是否具有统计学意义。

具体的检验步骤如下：

1. 提出零假设 \(H_0\) 和备择假设 \(H_1\)。
2. 根据实验数据计算统计量。
3. 根据统计量计算p值。
4. 将p值与显著性水平α进行比较。
5. 根据比较结果得出结论。

### 3.1.2 如何在研究报告中准确表述p值

在科学研究报告中，正确地表述p值非常重要。以下是撰写研究报告时的一些关键点：

- **清晰定义假设**：明确说明实验的零假设和备择假设是什么。
- **描述统计方法**：详细描述所使用的统计方法和分析过程。
- **展示p值结果**：报告中应展示p值的结果，并说明其意义。
- **解读统计显著性**：在p值基础上，解释实验结果是否统计显著，并讨论其科学含义。
- **谨慎语言使用**：避免使用绝对化的语言，强调统计结果只是在特定样本和条件下得到的结论。

## 3.2 p值在数据分析软件中的实现

### 3.2.1 使用R语言计算p值

R语言是一个强大的统计分析工具，可以方便地进行p值的计算。以下是一个使用R语言进行t检验并计算p值的示例代码：

# 示例数据集
data <- c(18.3, 19.7, 19.2, 21.4, 17.9,