p值解读误区:常见错误及避免策略
发布时间: 2024-11-22 16:40:15 阅读量: 44 订阅数: 31 


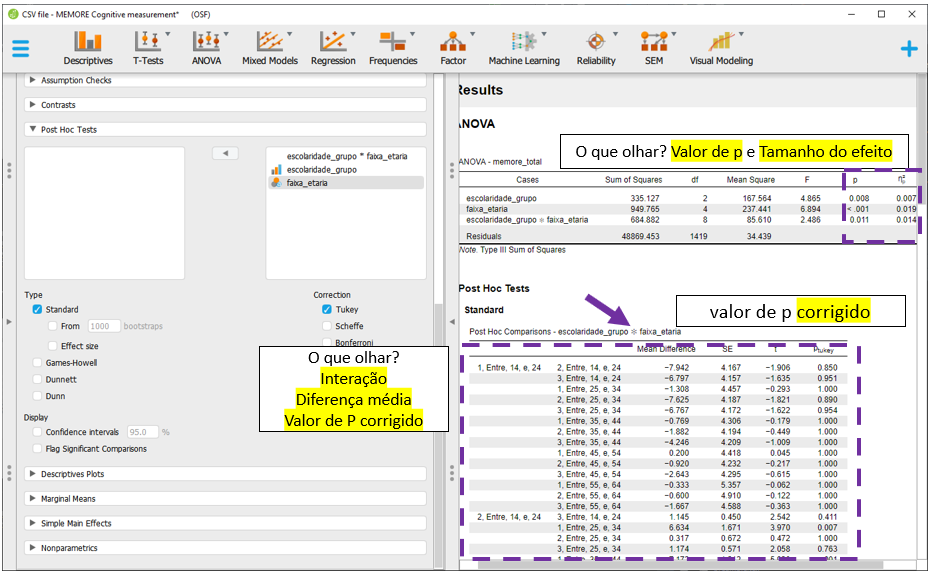
基于python实现计算两组数据P值
# 1. p值的基本概念与意义
在统计学中,p值是用来评估观测到的数据在零假设为真的情况下出现的概率。它的核心价值在于帮助研究者判断数据提供的证据强度。p值通常与一个预定的显著性水平(alpha水平)进行比较,以决定是否拒绝零假设。
## 1.1 p值的定义
p值是一个介于0和1之间的数值,表示在零假设成立的前提下,观测到当前结果或者更极端结果的概率。它并不是研究结果真实概率的直接度量,而是一种逆概率思维。
## 1.2 p值的意义
一个较低的p值表明,观测到的数据在零假设真实的情况下是不太可能发生的。这通常被解释为对零假设的拒绝,暗示可能存在的效应或关系。然而,它并不能证明这种关系就一定是因果关系,也不能提供效应大小的信息。
## 1.3 p值的误解
对p值的误解可能导致错误的结论。p值并不等同于发现效应的概率,也不能反映出效应的大小,它仅是一个统计学工具,必须谨慎使用,并且结合其他统计信息和实际背景来解释。
```markdown
[注意] 在接下来的章节中,我们将探讨p值解读的常见错误,并提出避免这些错误的策略,以确保科学结论的准确性。
```
# 2. p值解读中的常见错误
## 2.1 混淆p值与效应大小
### 2.1.1 理解p值与效应大小的关系
混淆p值和效应大小是统计推断中最常见的错误之一。p值表示在零假设(null hypothesis)为真的条件下,观察到当前样本结果或更极端结果的概率。而效应大小(effect size)是指研究中变量之间关系的实际强度或重要性。p值低并不意味着效应大小大;同样,效应大小大也不一定导致p值小。
举例来说,研究者在进行一个药物疗效的实验时,可能得到一个非常小的p值,表明药物效果显著,但这并不提供药物效果有多大的信息。如果样本量非常大,甚至极小的效应也可能产生统计显著性。因此,为了全面评价实验结果,研究者不仅需要关注p值,还要评估效应大小。
### 2.1.2 避免仅依赖p值的统计推断
为了更好地理解研究结果,仅依赖于p值来进行统计推断是不够的。应结合效应大小、置信区间等其他统计指标来进行综合评价。研究者应当报告效应大小,例如,Cohen's d用于度量均值差异的效应大小,相关系数r用于度量变量间的关联度。此外,研究者还应当注意测量误差、样本量以及样本选择偏差等因素的影响。
## 2.2 p值的误用与过度解释
### 2.2.1 p值不是发现真值的绝对指标
统计显著性并不意味着实际效应就是显著的,它反映的是在统计上可观察到的效果。p值很小,并不直接等同于效应在现实中是显著的或者有实际意义的。研究者常常误将统计显著性解释为实际效应显著,这是对p值的一种误用。
在决策过程中,仅依赖p值可能会忽略实际效应的存在,尤其是在样本量不足的情况下。例如,当一个实验的p值刚好为0.05时,意味着在100次相同实验中,我们有5次的几率得到与当前结果等同或更极端的结果,即使零假设实际上是真的。因此,p值既不是发现"真值"的绝对指标,也不应被用作决策的唯一依据。
### 2.2.2 p值与统计显著性的区别
统计显著性经常与p值混淆。p值表示的是数据观测结果在零假设下出现的概率,而统计显著性是一个更宽泛的概念,是指研究结果在统计上有意义,即结果不太可能是由随机误差造成的。统计显著性通常与显著性水平(如α=0.05)相比较,以判断是否拒绝零假设。
研究者应当明确,即使p值很小,也不能保证统计显著性就是实际显著性。例如,当研究的样本量非常大时,即使效应非常微小,p值也可能非常小,导致过度解释统计显著性。
### 2.2.3 避免“胜者诅咒”与p值操纵
“胜者诅咒”是指在多个研究中,只有那些结果显著的研究才被发表和认可,而不显著的研究则被忽略或隐藏,从而造成对某现象或效应的过度乐观评估。这种现象在科研领域普遍存在,会导致科学知识积累的偏差。
为了减少“胜者诅咒”,研究者应避免对p值的操纵,例如通过选择性报告、数据挖掘、HARKing(Hypothesizing After the Results are Known,即结果后假设)等不道德的研究实践。应该报告所有研究结果,无论其统计显著性如何,并且透明地公开研究设计、数据收集和分析过程。
## 2.3 p值计算的假设条件
### 2.3.1 检验的假设前提理解
进行假设检验时,通常需要一些前提假设,比如正态性、方差齐性等。这些假设条件是推断统计学的基础,违反这些假设条件可能会导致p值的误解。
例如,在进行t检验时,一般要求数据符合正态分布且方差相等。如果数据明显偏离正态分布或者两组方差差异很大,此时直接计算出的p值可能不可靠。在这种情况下,研究者应使用非参数检验方法或先进行数据转换。
### 2.3.2 假设条件违反时的p值解读
在假设条件被违反时,仍进行传统的统计检验并依据该检验的p值来做推断是不恰当的。此时得到的p值可能会误导研究者。
当数据不满足检验的前提假设时,可以采取以下几种策略:1)对数据进行变换,使之更符合假设条件;2)使用非参数统计方法,如曼-惠特尼U检验(Mann-Whitney U test)代替t检验;3)利用自助法(bootstrap methods)对统计量进行重采样以估计p值。这些方法可以在不同程度上缓解违反假设条件时的统计问题。
```markdown
表:假设检验的常见类型及前提假设
| 检验方法 | 前提假设 | 适用情况 |
|----------|----------|----------|
| t检验 | 正态分布,方差齐性 | 两组独立样本均值比较 |
| 方差分析 | 正态分布,方差齐性 | 三组或以上独立样本均值比较 |
| 卡方检验 | 分类数据的独立性 | 分类数据的频率分布比较 |
| 非参数检验 | 无需正态分布假设 | 样本量小、数据不满足正态分布的情况 |
```
通过表格,可以清晰地看到不同检验方法对应的假设条件以及它们的适用情况,从而在进行统计分析时选择合适的检验方法。
```mermaid
graph TD
A[开始统计分析] --> B{数据是否符合正态分布}
B -->|是| C[进行参数检验]
B -->|否| D{是否可以进行数据转换}
D -->|是| E[转换数据后进行参数检验]
D -->|否| F[进行非参数检验]
C --> G[计算并解读p值]
E --> G
F --> G
```
在上述mermaid流程图中,我们可以看到一个关于如何根据数据特点选择合适的统计检验方法的决策路径。
通过上述内容的讨论,我们可以看到p值解读中常见错误的产生原因及其纠正方法,有助于研究者更加准确地使用统计工具进
0
0





