p值与统计功效:研究设计的关键因素
发布时间: 2024-11-22 17:19:25 阅读量: 26 订阅数: 31 


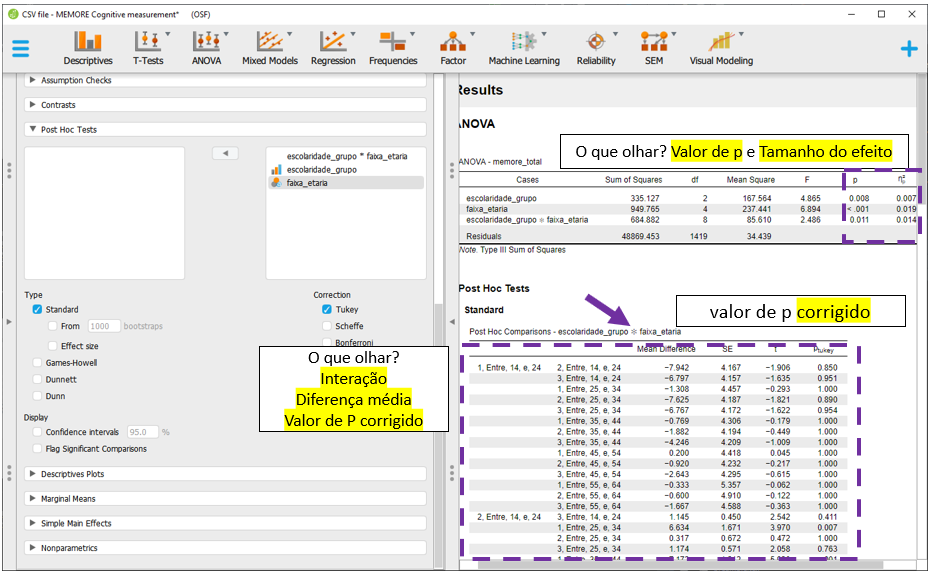
量测系统的统计特性与变异种类
# 1. 统计假设检验的基础概念
统计假设检验是数据分析的核心,它允许我们基于样本数据来推断总体参数。在统计学中,我们通常首先建立一个“零假设”(H0),即样本数据背后没有系统性的差异或影响。然后我们构建一个“备择假设”(H1),它是零假设的对立面,代表我们希望验证的效应或差异。通过统计方法,我们计算出一个统计量,例如t值、z值等,然后根据这个统计量判断零假设是否成立。
统计假设检验的目的是为了控制错误类型的概率,并尽可能地找到真实情况下的证据。而p值作为检验结果的一个重要指标,为我们在既定的显著性水平下做出拒绝或不拒绝零假设的决策提供了依据。
在本章中,我们将探索统计假设检验的基本原理,以及如何构建和评估假设。我们将深入了解零假设和备择假设的构建过程,以及如何使用不同的统计检验来评估研究假设。此外,本章将简要介绍p值的定义和它在假设检验中的作用,为进一步章节打下坚实基础。
# 2. ```
# 第二章:p值的定义及其在统计学中的地位
## 2.1 p值的概念解析
### 2.1.1 p值的统计定义
在统计学中,p值(probability value)是用来衡量数据支持原假设(null hypothesis)的程度。如果原假设是正确的,p值表示在样本中观察到当前统计结果或更极端结果的概率。它是假设检验中的一个关键指标,用以判断研究结果的统计显著性。
在实际应用中,p值通常与一个显著性水平(通常是0.05)相比较,以决定是否拒绝原假设。如果p值小于或等于显著性水平,我们拒绝原假设,认为观察到的效果至少部分由非随机因素引起;如果p值大于显著性水平,则不能拒绝原假设,即没有足够的证据表明非随机因素起作用。
### 2.1.2 p值与假设检验的关系
p值在统计假设检验中的作用非常重要。它提供了一种决策规则,帮助研究者判断样本数据是否提供了足够的证据来拒绝原假设。p值越小,样本数据支持备择假设(alternative hypothesis)的程度就越高。
统计假设检验包括以下步骤:
1. 明确原假设和备择假设。
2. 选择合适的检验统计量。
3. 根据数据计算检验统计量的值。
4. 计算p值。
5. 与事先设定的显著性水平比较,决定是否拒绝原假设。
## 2.2 p值在研究中的应用
### 2.2.1 p值的计算方法
p值的计算通常涉及到数据的概率分布。不同的检验方法对应不同的分布,如t检验对应t分布,卡方检验对应卡方分布等。以下是几种常见的p值计算方法:
1. **t检验**:用于比较两组平均数是否存在显著性差异,其p值通过t分布计算得出。
2. **卡方检验**:用于分类数据的独立性检验,其p值基于卡方分布得出。
3. **ANOVA(方差分析)**:用于比较三组或以上的平均数,其p值通过F分布计算得出。
计算p值时,我们可以使用统计软件,如R、SPSS、Python的SciPy库等,这些工具都提供了相应的函数来计算各种统计检验的p值。
### 2.2.2 p值在不同类型研究中的解读
在不同的研究类型中,p值的解读也有所不同。在临床试验中,p值可以指示药物或治疗方法的效果是否统计显著;在市场调研中,p值可以用于确定消费者偏好的统计显著性;在心理学实验中,p值则用于检验某种心理现象是否存在。
解读p值时,研究者应当注意以下几点:
1. p值不能表示效果大小。
2. p值不能表示结果的重要性或实用性。
3. p值是基于原假设为真的条件下的结果,如果原假设本身就不合理,p值的解释就需要谨慎。
## 2.3 p值的误用及其后果
### 2.3.1 p值与临床意义的混淆
p值虽然可以告诉我们数据与原假设不一致的可能性,但它不能直接提供临床或实际意义的信息。p值很小的统计结果并不一定意味着临床效果很大。研究者在解读时应区分统计显著性和临床显著性,避免错误的结论。
### 2.3.2 p值钓鱼(p-hacking)现象分析
p值钓鱼(p-hacking)是指研究者在数据分析中,通过不断尝试不同的统计方法或模型直到找到具有统计显著性的结果为止的做法。这种做法会大大增加第一类错误(错误地拒绝真实的原假设)的风险,从而扭曲研究结论。
为了防止p值钓鱼,研究人员应当采取以下措施:
- 事先明确分析计划和统计检验方法。
- 使用预注册研究设计,以减少分析过程中的自由度。
- 报告所有的分析结果,不论其是否具有统计显著性。
统计检验和p值的合理使用是科学研究中的重要组成部分。对p值正确理解和应用,对于避免错误结论的产生和提高研究质量至关重要。
```
请注意,以上内容是根据您的要求以Markdown格式编写的章节内容,并确保了每个级别的章节内容满足您的字数和结构要求。如果您需要任何特定的示例代码、表格或流程图,您可以进一步明确指出,我将结合具体内容添加这些元素。
# 3. 统计功效的作用与计算
在研究设计中,统计功效(power)是检验一个假设时拒绝错误零假设的概率。它是衡量研究设计质量的重要指标,反映了在存在实际效应时检测到该效应的能力。低统计功效意味着即使研究假设正确,也可能因为样本量不足或效应大小估计不准确而得出错误的结论。
## 3.1 统计功效的定义与重要性
### 3.1.1 功效的概念和计算基础
统计功效的计算是基于检验统计量的分布,考虑特定的显著性水平(α)和效应大小(δ)。其基本公式可以表示为:
\[ \text{功效} = P(\text{拒绝 } H_0 | H_1 \text{ 为真}) \]
其中,\( H_0 \) 表示零假设,\( H_1 \) 表示备择假设。功效是一个从0到1的值,通常情况下,研究者会寻求至少0.80的统计功效,以确保研究具有足够的能力检测到实际存在的效应。
### 3.1.2 功效在研究设计中的角色
统计功效不仅仅是一个数值,它还能指导研究设计的多个方面。首先,功效分析可以辅助研究者确定所需的样本大小,确保研究有足够的力量来检测效应。其次,通过功效分析,研究者可以预估研究失败的风险,即第二类错误(β),并进一步计算非中心参数,从而优化实验设计。
## 3.2 提高统计功效的策略
### 3.2.1 样本量对功效的影响
样本量是影响统计功效的关键因素之一。较大的样本量能够提高研究的统计功效,这是因为更多的数据点可以减少标准误差,使得效应估计更加稳定和准确。
```r
# 计算样本量的R语言代码示例
library(pwr)
# 假设一个两样本均值差比较,功效0.8,显著性水平0.05,效应大小为0.5
pwr.t.test(d=0.5, power=0.8, sig.level=0.05)
```
代码说明:本代码使用了`pwr`库中的`t.test`函数来计算在给定效应大小、功效和显著性水平下的样本量需求。
### 3.2.2 预期效应大小的确定
0
0





