MATLAB稀疏数组：高效存储和处理稀疏数据的技术，提升代码的内存效率

# 1. MATLAB稀疏数组简介

稀疏数组是一种专门用于存储和处理稀疏数据的特殊数据结构，其中大部分元素为零。在实际应用中，许多数据都具有稀疏性，例如图论中的邻接矩阵、机器学习中的特征矩阵等。MATLAB中提供了丰富的稀疏数组功能，可以高效地处理和分析这些数据。

稀疏数组的存储格式与普通数组不同，采用专门的压缩格式来节省内存空间。MATLAB支持多种稀疏数组存储格式，包括坐标格式（COO）、压缩行存储格式（CSR）和压缩列存储格式（CSC）。这些格式各有优缺点，根据具体应用场景选择合适的格式可以提高计算效率。

# 2.1 稀疏性概念和表示

### 稀疏性的定义和度量

稀疏性描述了矩阵中非零元素相对于总元素数量的比例。一个稀疏矩阵是指其非零元素数量远少于总元素数量的矩阵。稀疏性的度量通常使用稀疏度（sparsity）来表示，定义为：

稀疏度 = 1 - (非零元素数量 / 总元素数量)

稀疏度范围从 0 到 1，其中 0 表示稠密矩阵（所有元素都非零），1 表示完全稀疏矩阵（所有元素都为零）。

### 稀疏矩阵的表示

稀疏矩阵可以用各种方式表示，以有效地存储和操作非零元素。最常见的表示形式包括：

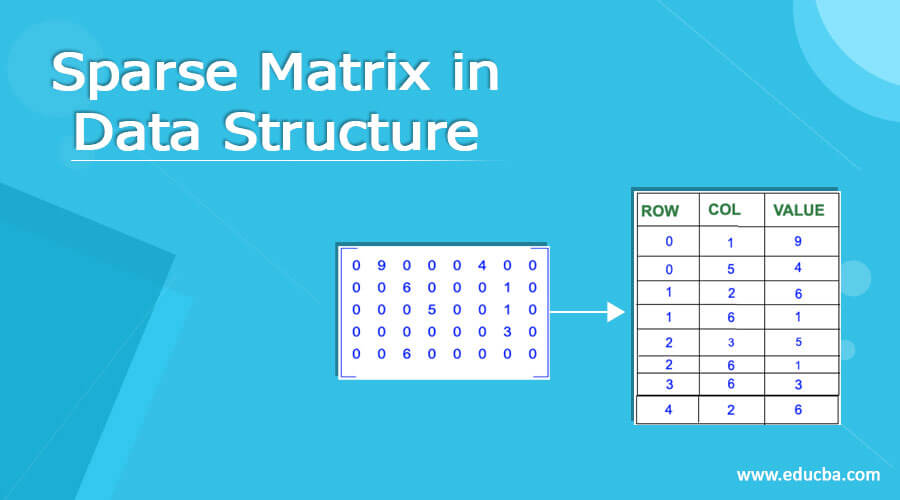
- **坐标格式（COO）**：存储非零元素的行列索引和值。
- **压缩行存储格式（CSR）**：存储每个行的非零元素的列索引和值，以及每行非零元素的起始位置。
- **压缩列存储格式（CSC）**：存储每个列的非零元素的行索引和值，以及每列非零元素的起始位置。

### 不同表示形式的比较

不同表示形式的优缺点如下：

| 表示形式 | 优点 | 缺点 |
|---|---|---|
| COO | 存储紧凑，易于插入和删除元素 | 随机访问效率低 |
| CSR | 随机访问行元素效率高 | 存储开销较大 |
| CSC | 随机访问列元素效率高 | 存储开销较大 |

选择合适的表示形式取决于稀疏矩阵的特性和预期操作。对于随机访问行元素较多的应用，CSR 格式更合适；对于随机访问列元素较多的应用，CSC 格式更合适。

# 3. 稀疏数组的实践应用

### 3.1 稀疏矩阵的创建和操作

在 MATLAB 中创建稀疏矩阵有几种方法：

- **sparse 函数：**这是创建稀疏矩阵最常用的方法。它接受三个参数：行索引、列索引和非零元素值。例如：

A = sparse([1, 2, 3], [1, 2, 3], [1, 2, 3]);

- **spdiags 函数：**用于创建对角线非零的稀疏矩阵。它接受三个参数：对角线元素值、对角线偏移量和矩阵大小。例如：

A = spdiags([1, 2, 3], 0, 3, 3);

- **speye 函数：**创建单位稀疏矩阵，即对角线元素为 1 的稀疏矩阵。它接受一个参数：矩阵大小。例如：

A = speye(3);

稀疏矩阵的操作与普通矩阵类似，但由于其稀疏性，某些操作可能需要特殊处理。例如：

- **加法和减法：**稀疏矩阵的加法和减法与普通矩阵相同。
- **乘法：**稀疏矩阵的乘法需要使用专门的算法，如稀疏矩阵-稀疏矩阵乘法（SpGEMM）或稀疏矩阵-向量乘法（SpMV）。
- **转置：**稀疏矩阵的转置可以通过 `transpose` 函数或 `.'` 运算符获得。

### 3.2 稀疏矩阵的数值计算

稀疏矩阵的数值计算是其一项重要应用。它涉及到各种线性代数操作，如：

#### 3.2.1 基本算术运算

稀疏矩阵的基本算术运算包括加法、减法和乘法。这些运算与普通矩阵类似，但由于稀疏性，需要使用专门的算法。例如，稀疏矩阵的乘法可以使用稀疏矩阵-稀疏矩阵乘法（SpGEMM）算法。

#### 3.2.2 矩阵分解

矩阵分解是稀疏矩阵数值计算中的一个重要工具。它可以将稀疏矩阵分解为更简单的形式，从而简化后续的计算。常用的矩阵分解包括：

- **LU 分解：**将稀疏矩阵分解为下三角矩阵和上三角矩阵的乘积。
- **QR 分解：**将稀疏矩阵分解为正交矩阵和上三角矩阵的乘积。
- **奇异值分解（SVD）：**将稀疏矩阵分解为三个矩阵的乘积：左奇异值矩阵、奇异值矩阵和右奇异值矩阵。

### 3.3