揭秘MATLAB数组：类型、维度和操作，掌握数据访问艺术

# 1. MATLAB数组基础**

MATLAB数组是MATLAB中用于存储和操作数据的基本数据结构。数组是一个有序的元素集合，每个元素都具有相同的数据类型。数组可以是一维、二维或多维的，并且可以存储各种类型的数据，包括数值、字符和逻辑值。

**数组创建与初始化**

MATLAB中可以通过多种方式创建和初始化数组：

* 使用内置函数：MATLAB提供了许多内置函数来创建特定类型的数组，例如`zeros`、`ones`和`rand`。
* 手动赋值：可以使用方括号`[]`手动为数组元素赋值。例如：`A = [1, 2, 3; 4, 5, 6]`创建一个二维数组。

# 2. MATLAB数组类型与维度

MATLAB中的数组是数据的基本存储单元，它可以存储各种类型和维度的元素。本章节将深入探讨MATLAB数组的类型和维度，为更高级别的数组操作奠定基础。

### 2.1 数值类型与数据表示

MATLAB支持多种数值类型，每种类型都使用不同的数据表示形式，从而影响其存储容量和精度。

#### 2.1.1 整数类型

整数类型用于存储整数值，包括有符号整数和无符号整数。有符号整数使用补码表示，而无符号整数使用原码表示。MATLAB提供了以下整数类型：

| 类型 | 字节 | 范围 |
|---|---|---|
| `int8` | 1 | -128 ~ 127 |
| `int16` | 2 | -32768 ~ 32767 |
| `int32` | 4 | -2147483648 ~ 2147483647 |
| `int64` | 8 | -9223372036854775808 ~ 9223372036854775807 |

#### 2.1.2 浮点数类型

浮点数类型用于存储小数或实数。MATLAB提供了以下浮点数类型：

| 类型 | 字节 | 精度 | 范围 |
|---|---|---|---|
| `single` | 4 | 6-7位 | ±1.175494351e-38 ~ ±3.402823466e+38 |
| `double` | 8 | 15-16位 | ±2.2250738585072014e-308 ~ ±1.7976931348623157e+308 |

#### 2.1.3 复数类型

复数类型用于存储复数，它由实部和虚部组成。MATLAB提供了以下复数类型：

| 类型 | 字节 | 范围 |
|---|---|---|
| `complex` | 16 | 实部和虚部均为`double`类型 |

### 2.2 数组维度与形状

MATLAB数组的维度是指数组中元素的排列方式。MATLAB支持一维、二维和多维数组。

#### 2.2.1 一维数组

一维数组是一个线性序列，其元素按顺序排列。一维数组的维度为1，形状为`[1, n]`，其中`n`为数组元素个数。

#### 2.2.2 二维数组

二维数组是一个矩阵，其元素按行和列排列。二维数组的维度为2，形状为`[m, n]`，其中`m`为行数，`n`为列数。

#### 2.2.3 多维数组

多维数组是具有三个或更多维度的数组。多维数组的维度和形状由`size()`函数返回。例如，一个三维数组的维度为3，形状为`[m, n, p]`，其中`m`为第一维度的长度，`n`为第二维度的长度，`p`为第三维度的长度。

**代码块：**

% 创建一维数组
a = [1, 2, 3, 4, 5];

% 创建二维数组
b = [1, 2, 3; 4, 5, 6; 7, 8, 9];

% 创建三维数组
c = [1, 2, 3; 4, 5, 6; 7, 8, 9];
c = reshape(c, [1, 3, 3]);

% 查看数组维度和形状
disp(['一维数组a的维度：', num2str(ndims(a))]);
disp(['一维数组a的形状：', num2str(size(a))]);
disp(['二维数组b的维度：', num2str(ndims(b))]);
disp(['二维数组b的形状：', num2str(size(b))]);
disp(['三维数组c的维度：', num2str(ndims(c))]);
disp(['三维数组c的形状：', num2str(size(c))]);

**逻辑分析：**

* `ndims()`函数返回数组的维度。
* `size()`函数返回数组的形状，即每个维度上的元素个数。
* `reshape()`函数可以改变数组的形状，而不改变元素的顺序。

**参数说明：**

* `ndims()`函数没有参数。
* `size()`函数的参数是数组本身。
* `reshape()`函数的参数包括数组本身、新的形状。

# 3. MATLAB数组操作**

### 3.1 数组创建与初始化

MATLAB提供多种方法创建和初始化数组：

#### 3.1.1 使用内置函数

* **zeros()：**创建指定大小的数组，元素值全部为0。
* **ones()：**创建指定大小的数组，元素值全部为1。
* **eye()：**创建单位矩阵，对角线元素为1，其余元素为0。
* **rand()：**创建指定大小的数组，元素值是[0, 1)之间的随机数。
* **randn()：**创建指定大小的数组，元素值是正态分布的随机数。

**示例：**

% 创建一个5行3列的零矩阵
A = zeros(5, 3);

% 创建一个4行4列的单位矩阵
B = eye(4);

% 创建一个3行5列的随机数矩阵
C = rand(3, 5);

#### 3.1.2 手动赋值

也可以使用赋值操作符手动创建和初始化数组：

% 创建一个包含元素[1, 2, 3]的数组
D = [1, 2, 3];

% 创建一个包含多行多列元素的数组
E = [
    1, 2, 3;
    4, 5, 6;
    7, 8, 9
];

### 3.2 数组索引与切片

MATLAB使用索引和切片机制访问和操作数组中的元素：

#### 3.2.1 线性索引

线性索引将多维数组视为一维数组，使用单个索引值访问元素。

% 获取数组A中第2行第3列的元素
element = A(2, 3);

#### 3.2.2 多维索引

多维索引使用多个索引值访问多维数组中的元素。

% 获取数组E中第2行第3列的元素
element = E(2, 3);

#### 3.2.3 切片操作

切片操作允许一次获取数组的多个元素，使用冒号(:)或索引范围。

% 获取数组A中第2行所有元素
row2 = A(2, :);

% 获取数组E中第2行第2列到第4列的元素
subarray = E(2, 2:4);

### 3.3 数组运算

MATLAB支持对数组进行各种运算，包括：

#### 3.3.1 算术运算

* 加法(+)：数组元素逐个相加。
* 减法(-)：数组元素逐个相减。
* 乘法(*)：数组元素逐个相乘。
* 除法(/)：数组元素逐个相除。

**示例：**

% 对数组A和B进行加法运算
C = A + B;

% 对数组E进行乘法运算
F = E * 2;

#### 3.3.2 逻辑运算

* 与(&)：数组元素逐个进行逻辑与运算。
* 或(|)：数组元素逐个进行逻辑或运算。
* 非(~)：对数组元素进行逻辑非运算。

**示例：**

% 对数组A和B进行逻辑与运算
G = A & B;

% 对数组E进行逻辑非运算
H = ~E;

#### 3.3.3 关系运算

* 等于(==)：比较数组元素是否相等。
* 不等于(~=)：比较数组元素是否不相等。
* 大于(>)：比较数组元素是否大于。
* 小于(<)：比较数组元素是否小于。
* 大于等于(>=)：比较数组元素是否大于等于。
* 小于等于(<=)：比较数组元素是否小于等于。

**示例：**

% 比较数组A和B是否相等
I = A == B;

% 比较数组E中元素是否大于5
J = E > 5;

# 4. MATLAB数组高级操作

### 4.1 数组连接与合并

#### 4.1.1 水平连接（cat）

水平连接（`cat`）函数用于将多个数组沿指定维度连接在一起。语法如下：

cat(dim, A1, A2, ..., An)

其中：

* `dim`：连接维度，取值范围为 1（行连接）或 2（列连接）
* `A1, A2, ..., An`：要连接的数组

**示例：**

A = [1 2 3; 4 5 6];
B = [7 8 9; 10 11 12];

% 水平连接（行连接）
C = cat(1, A, B);
% 输出：
% C =
%     1     2     3
%     4     5     6
%     7     8     9
%    10    11    12

% 水平连接（列连接）
D = cat(2, A, B);
% 输出：
% D =
%     1     2     3     7     8     9
%     4     5     6    10    11    12

#### 4.1.2 垂直连接（vertcat）

垂直连接（`vertcat`）函数是`cat`函数的特殊情况，用于将多个数组沿第一维度（行）连接在一起。语法如下：

vertcat(A1, A2, ..., An)

**示例：**

A = [1 2 3; 4 5 6];
B = [7 8 9; 10 11 12];

% 垂直连接
C = vertcat(A, B);
% 输出：
% C =
%     1     2     3
%     4     5     6
%     7     8     9
%    10    11    12

#### 4.1.3 合并数组（reshape）

合并数组（`reshape`）函数用于改变数组的形状，将一个多维数组合并成一个一维数组或将一个一维数组展开成一个多维数组。语法如下：

reshape(A, new_shape)

其中：

* `A`：要合并的数组
* `new_shape`：合并后的数组形状，是一个行向量，指定新数组的行数、列数等维度

**示例：**

A = [1 2 3; 4 5 6; 7 8 9];

% 将A合并成一维数组
B = reshape(A, 1, 9);
% 输出：
% B =
%     1     2     3     4     5     6     7     8     9

% 将B展开成三维数组
C = reshape(B, 3, 3, 1);
% 输出：
% C =
%     1     2     3
%     4     5     6
%     7     8     9

### 4.2 数组转换与类型转换

#### 4.2.1 类型转换（typecast）

类型转换（`typecast`）函数用于将一个数组中的数据从一种数据类型转换为另一种数据类型。语法如下：

typecast(A, new_type)

其中：

* `A`：要转换的数组
* `new_type`：要转换到的数据类型，可以是`'int8'、'int16'、'int32'、'int64'、'uint8'、'uint16'、'uint32'、'uint64'、'single'、'double'、'logical'`等

**示例：**

A = [1 2 3; 4 5 6];

% 将A中的数据从int32转换为double
B = typecast(A, 'double');
% 输出：
% B =
%     1.0000    2.0000    3.0000
%     4.0000    5.0000    6.0000

#### 4.2.2 维度转换（squeeze、expand）

维度转换函数用于改变数组的维度。`squeeze`函数用于去除数组中多余的维度，而`expand`函数用于增加数组的维度。

**squeeze**

语法：

squeeze(A)

**示例：**

A = [1 2 3; 4 5 6];

% 去除A中的多余维度
B = squeeze(A);
% 输出：
% B =
%     1     2     3
%     4     5     6

**expand**

语法：

expand(A, dim, n)

其中：

* `dim`：要增加维度的维度
* `n`：要增加的维度数

**示例：**

A = [1 2 3; 4 5 6];

% 在A的第二维度增加一个维度
B = expand(A, 2, 1);
% 输出：
% B =
%     1     2     3
%     4     5     6
%     NaN    NaN    NaN

### 4.3 数组函数与特殊操作

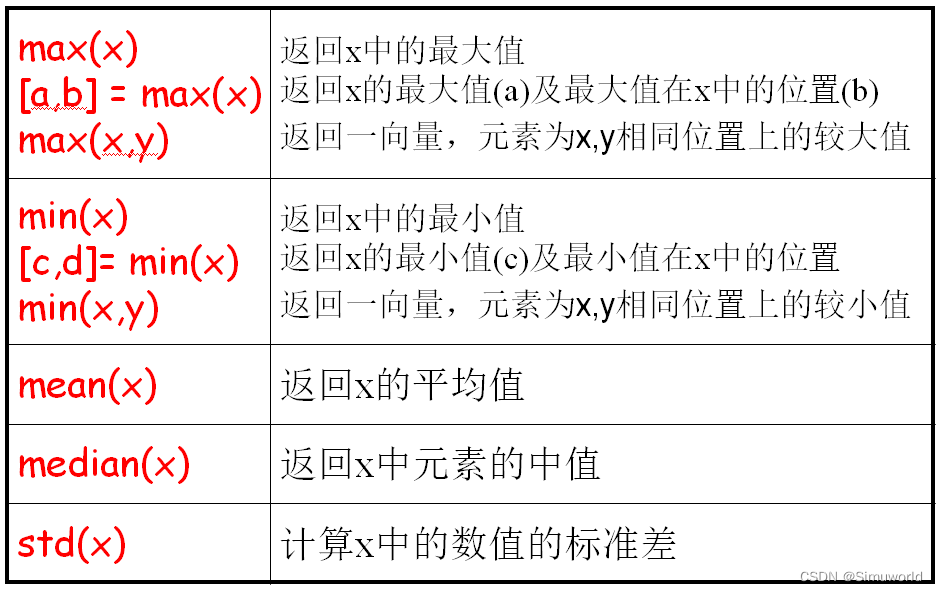
#### 4.3.1 统计函数（mean、std）

统计函数用于对数组中的数据进行统计计算。

**mean**

语法：

mean(A)

**示例：**

A = [1 2 3; 4 5 6];

% 计算A中的平均值
B = mean(A);
% 输出：
% B =
%     3.5000

**std**

语法：

std(A)

**示例：**

A = [1 2 3; 4 5 6];

% 计算A中的标准差
B = std(A);
% 输出：
% B =
%     1.8708

#### 4.3.2 排序函数（sort、unique）

排序函数用于对数组中的数据进行排序。

**sort**

语法：

sort(A)

**示例：**

A = [3 1 2 5 4];

% 对A中的数据进行升序排序
B = sort(A);
% 输出：
% B =
%     1     2     3     4     5

**unique**

语法：

unique(A)

**示例：**

A = [1 2 3 2 4 5 1];

% 找出A中的唯一元素
B = unique(A);
% 输出：
% B =
%     1     2     3     4     5

#### 4.3.3 逻辑函数（any、all）

逻辑函数用于对数组中的逻辑值进行操作。

**any**

语法：

any(A)

**示例：**

A = [true false true; false true false];

% 检查A中是否存在任何真值
B = any(A);
% 输出：
% B =
%     1     1

**all**

语法：

all(A)

**示例：**

A = [true false true; true true true];

% 检查A中是否所有元素都为真值
B = all(A);
% 输出：
% B =
%     0     1

# 5.1 数据分析与可视化

MATLAB在数据分析和可视化方面提供了强大的工具，可以帮助用户轻松高效地处理和展示数据。

### 5.1.1 数据统计与图表绘制

MATLAB提供了丰富的统计函数，可以对数据进行各种统计分析，如求取均值、标准差、方差等。此外，MATLAB还提供了多种图表绘制函数，如`plot`、`bar`、`scatter`等，可以将数据以直观的方式展示出来。

% 数据统计
data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
mean_value = mean(data);
std_value = std(data);
disp(['Mean: ', num2str(mean_value)]);
disp(['Standard Deviation: ', num2str(std_value)]);

% 图表绘制
figure;
plot(data, 'b-o');  % 蓝色实线和圆形标记
xlabel('Index');
ylabel('Value');
title('Data Plot');
grid on;

### 5.1.2 图像处理与分析

MATLAB在图像处理和分析方面也具有强大的功能。它提供了各种图像处理工具，如图像读取、转换、增强、分割等。此外，MATLAB还提供了图像分析工具，如边缘检测、特征提取、模式识别等。

% 图像读取
image = imread('image.jpg');

% 图像转换
gray_image = rgb2gray(image);  % 转换为灰度图像

% 图像增强
enhanced_image = imadjust(gray_image, [0.2, 0.8]);  % 调整对比度

% 图像分析
edges = edge(enhanced_image, 'canny');  % Canny边缘检测

% 显示结果
figure;
subplot(1, 3, 1);
imshow(image);
title('Original Image');
subplot(1, 3, 2);
imshow(gray_image);
title('Grayscale Image');
subplot(1, 3, 3);
imshow(edges);
title('Edge Detection');