矩阵乘法的历史发展：追溯矩阵乘法的发展历程，了解其演变和进步（历史发展大揭秘）

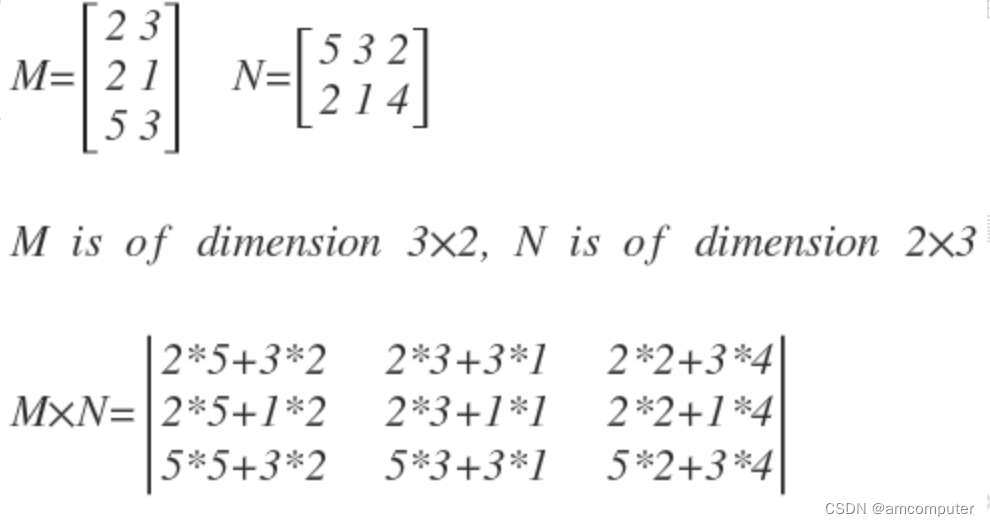
# 1. 矩阵乘法的概念和理论基础

矩阵乘法是一种数学运算，用于将两个矩阵相乘，产生一个新的矩阵。矩阵乘法的概念可以追溯到 19 世纪，当时数学家们开始研究线性代数。

矩阵乘法的基本原理是将第一个矩阵的每一行与第二个矩阵的每一列相乘，然后将结果相加。例如，如果 A 是一个 m×n 矩阵，B 是一个 n×p 矩阵，那么 A 与 B 的乘积 C 将是一个 m×p 矩阵。

矩阵乘法的理论基础建立在线性代数的原理之上。矩阵乘法满足结合律和分配律，并且可以用来表示线性变换。矩阵乘法在许多数学和科学领域都有着广泛的应用，包括求解线性方程组、图像处理和机器学习。

# 2. 矩阵乘法的历史发展

### 2.1 古代数学家的探索

矩阵乘法的概念最早可以追溯到公元前 1900 年的古巴比伦，当时数学家们使用泥板记录线性方程组的解法。这些解法本质上涉及矩阵乘法，尽管当时尚未明确定义矩阵的概念。

### 2.2 19 世纪的突破性进展

19 世纪，矩阵的概念正式诞生。1858 年，英国数学家凯莱（Arthur Cayley）提出了矩阵的现代定义，并将其命名为“矩阵”。此后，矩阵乘法作为线性代数中的一个基本运算，得到了广泛的研究。

1897 年，英国数学家西尔维斯特（James Joseph Sylvester）提出了“行列式”的概念，为矩阵乘法的性质和应用奠定了基础。行列式可以用来判断矩阵是否可逆，并计算矩阵的行列式值，这在求解线性方程组和计算矩阵的特征值时至关重要。

### 2.3 20 世纪的算法优化

20 世纪，矩阵乘法的算法不断优化。1969 年，德国数学家斯特拉森（Volker Strassen）提出了著名的“斯特拉森算法”，将矩阵乘法的复杂度从 O(n^3) 降低到 O(n^2.81)。斯特拉森算法通过将矩阵划分为更小的子矩阵，并使用递归的方式进行乘法运算，实现了算法的优化。

def strassen(A, B):
    """
    斯特拉森矩阵乘法算法

    参数：
        A：矩阵 A
        B：矩阵 B

    返回：
        矩阵 A 和 B 的乘积
    """

    n = len(A)
    if n <= 32:
        return numpy.dot(A, B)

    # 将矩阵划分为四个子矩阵
    A11 = A[:n // 2, :n // 2]
    A12 = A[:n // 2, n // 2:]
    A21 = A[n // 2:, :n // 2]
    A22 = A[n // 2:, n // 2:]

    B11 = B[:n // 2, :n // 2]
    B12 = B[:n // 2, n // 2:]
    B21 = B[n // 2:, :n // 2]
    B22 = B[n // 2:, n // 2:]

    # 计算子矩阵的乘积
    M1 = strassen(A11 + A22, B11 + B22)
    M2 = strassen(A21 + A22, B11)
    M3 = strassen(A11, B12 - B22)
    M4 = strassen(A22, B21 - B11)
    M5 = strassen(A11 + A12, B22)
    M6 = strassen(A21 - A11, B11 + B12)
    M7 = strassen(A12 - A22, B21 + B22)

    # 组装结果矩阵
    C11 = M1 + M4 - M5 + M7
    C12 = M3 + M5
    C21 = M2 + M4
    C22 = M1 - M2 + M3 + M6

    return numpy.co