矩阵乘法的复杂度分析：深入理解矩阵乘法的时间和空间复杂度（复杂度大揭秘）

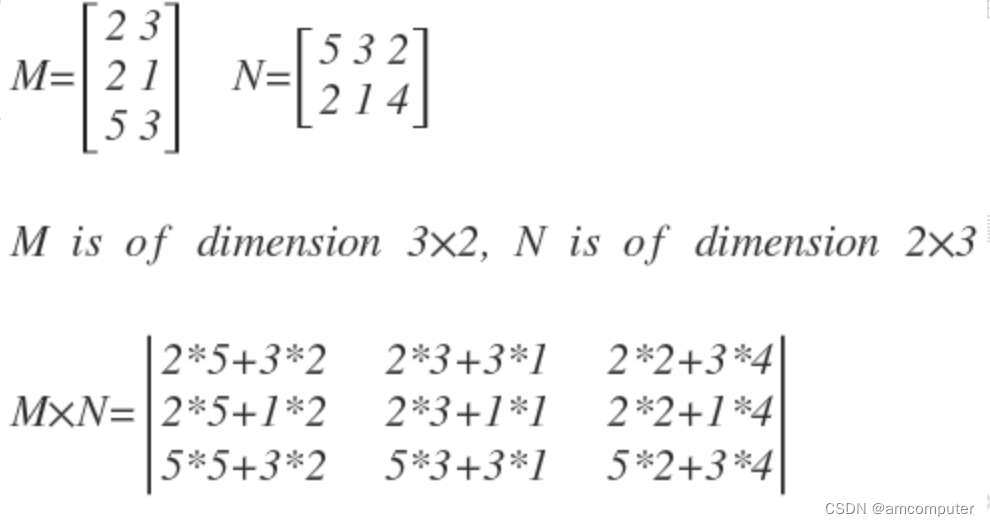
# 1. 矩阵乘法的基本概念**

矩阵乘法是线性代数中的一种基本运算，它将两个矩阵相乘，得到一个新的矩阵。矩阵乘法的定义如下：

C = A * B

其中：

* A 和 B 是两个矩阵
* C 是 A 和 B 相乘得到的矩阵

矩阵乘法的规则是：A 的第 i 行和 B 的第 j 列的元素相乘，然后将结果加到 C 的第 i 行和第 j 列的元素上。例如，以下矩阵 A 和 B 相乘：

A = [[1, 2], [3, 4]]
B = [[5, 6], [7, 8]]

则 C = A * B 为：

C = [[19, 22], [43, 50]]

# 2.1 矩阵乘法的时间复杂度

### 2.1.1 朴素算法

朴素算法是矩阵乘法最直接的实现方法，它按照矩阵乘法的定义逐行逐列计算每个元素。对于两个大小为 $m \times n$ 和 $n \times p$ 的矩阵 $A$ 和 $B$，朴素算法的时间复杂度为 $O(mnp)$。

def matrix_multiplication_naive(A, B):
    m, n = A.shape
    n, p = B.shape
    C = np.zeros((m, p))
    for i in range(m):
        for j in range(p):
            for k in range(n):
                C[i, j] += A[i, k] * B[k, j]
    return C

### 2.1.2 分治算法

分治算法将矩阵乘法分解为更小的子问题，从而降低时间复杂度。它采用递归的方式将矩阵划分为更小的块，直到块的大小为 $1 \times 1$，然后逐层计算子块的乘积并合并结果。

def matrix_multiplication_divide_and_conquer(A, B):
    m, n = A.shape
    n, p = B.shape

    if m == 1 or n == 1 or p == 1:
        return A @ B

    # 将矩阵 A 和 B 分成四个子块
    A11 = A[:m//2, :n//2]
    A12 = A[:m//2, n//2:]
    A21 = A[m//2:, :n//2]
    A22 = A[m//2:, n//2:]

    B11 = B[:n//2, :p//2]
    B12 = B[:n//2, p//2:]
    B21 = B[n//2:, :p//2]
    B22 = B[n//2:, p//2:]

    # 递归计算子块的乘积
    C11 = matrix_multiplication_divide_and_conquer(A11, B11)
    C12 = matrix_multiplication_divide_and_conquer(A11, B12)
    C21 = matrix_multiplication_divide_and_conquer(A21, B11)
    C22 = matrix_multiplication_divide_and_conquer(A21, B12)

    # 合并结果
    C = np.block([[C11, C12], [C21, C22]])
    return C

分治算法的时间复杂度为 $O(n^3 \log n)$，比朴素算法的 $O(mnp)$ 复杂度有了显著的降低。

# 3. 矩阵乘法的实践复杂度

### 3.1 不同算法的实践比较

#### 3.1.1 朴素算法

朴素算法的实践复杂度与矩阵大小呈三次方关系，即 $O(n^3)$。当矩阵规模较小时，朴素算法的运行时间尚可接受。但当矩阵规模增大时，朴素算法的运行时间将急剧增加，变得不可行。

def naive_matrix_multiplication(A, B):
    """
    朴素矩阵乘法算法

    参数：
        A：m x n 矩阵
        B：n x p 矩阵

    返回：
        C：m x p 矩阵
    """
    m, n = A.shape
    n, p = B.shape
    C = np.zeros((m, p))

    for i in ra