矩阵乘法的容错性：构建容错的矩阵乘法算法，提升系统可靠性（容错性大揭秘）

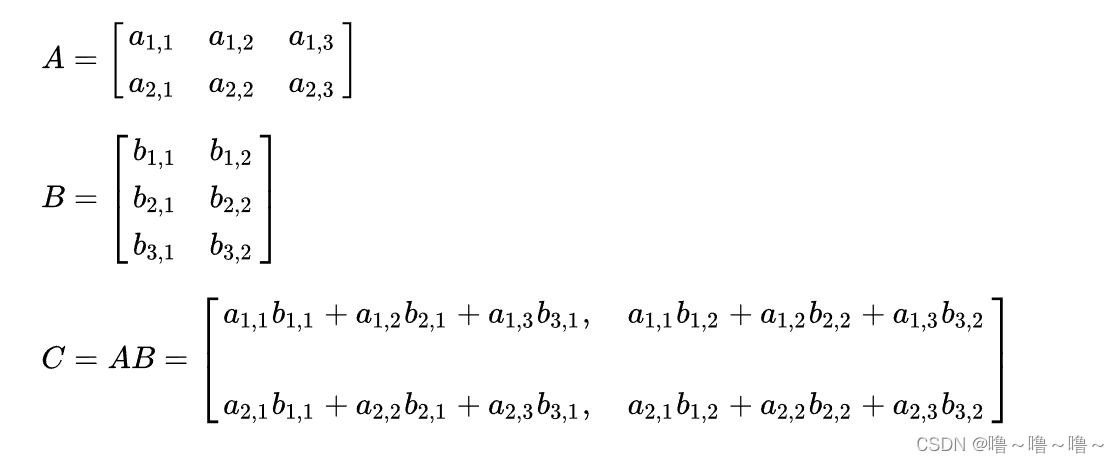
# 1. 矩阵乘法概述**

矩阵乘法是一种基本线性代数运算，用于计算两个矩阵的乘积。它在计算机图形学、机器学习和数据分析等领域有广泛的应用。矩阵乘法的基本定义如下：

给定两个矩阵 A 和 B，其中 A 的维度为 m×n，B 的维度为 n×p，它们的乘积 C 为 m×p 矩阵，其元素 c_ij 由以下公式计算：

c_ij = ∑(a_ik * b_kj)

其中，a_ik 表示矩阵 A 中第 i 行第 k 列的元素，b_kj 表示矩阵 B 中第 k 行第 j 列的元素。

# 2. 矩阵乘法容错性理论

### 2.1 容错性的概念和重要性

**容错性**是指系统在出现故障或错误时，仍能继续正常运行或维持一定水平的性能的能力。在矩阵乘法中，容错性至关重要，因为它可以确保即使在存在错误的情况下，矩阵乘法运算也能产生正确的结果。

### 2.2 矩阵乘法的容错性分析

矩阵乘法的容错性取决于以下因素：

- **错误类型：**错误可以是随机的（例如，数据损坏）或系统性的（例如，算法缺陷）。
- **错误位置：**错误可以发生在输入矩阵、乘法运算本身或输出矩阵中。
- **错误幅度：**错误可以是轻微的（例如，单个元素的错误）或严重的（例如，整个矩阵的丢失）。

根据这些因素，可以将矩阵乘法的容错性分为以下几个级别：

- **完全容错：**算法可以在任何错误情况下产生正确的结果。
- **部分容错：**算法可以在某些错误情况下产生正确的结果，但在其他情况下会失败。
- **不容错：**算法在任何错误情况下都会失败。

在实际应用中，完全容错的算法往往是不可行的，因此通常需要权衡容错性与算法复杂度和性能之间的关系。

# 3.1 容错矩阵乘法的基本原理

容错矩阵乘法算法的基本原理是通过引入冗余信息来增强矩阵乘法的容错性。具体来说，对于给定的两个矩阵 A 和 B，其乘积 C 可以表示为：

C = A * B

在容错矩阵乘法算法中，我们将 A 和 B 扩展为冗余矩阵 A' 和 B'，其中：

A' = [A, A_redundant]
B' = [B, B_redundant]

其中，`A_redundant` 和 `B_redundant` 是 A 和 B 的冗余部分，它们包含了 A 和 B 的部分信息。通过引入冗余信息，我们可以增强矩阵乘法算法的容错性，使其能够在存在错误的情况下仍然能够得到正确的结果。

### 3.2 容错矩阵乘法算法的实现

容错矩阵乘法算法的实现主要分为以下几个步骤：

1. **矩阵扩展：**将 A 和 B 扩展为冗余矩阵 A' 和 B'。
2. **矩阵乘法：**计算 A' 和 B' 的乘积 C'。
3. **错误检测：**检查 C' 中是否存在错误。
4. **错误恢复：**如果存在错误，则利用冗余信息恢复 C' 中的错误元素。
5. **结果输出：**输出恢复后的 C'，即为容错矩阵乘法的结果。

以下是一个使用 Python 实现的容错矩阵乘法算法示例：

import numpy as np

def fault_tolerant_matrix_multiplication(A, B):
    """
    容错矩阵乘法算法

    参数：
        A (numpy.ndarray): 矩阵 A
        B (numpy.ndarray): 矩阵 B

    返回：
        C (numpy.ndarray): 容错矩阵乘法的结果
    """

    # 矩阵扩展
    A_redundant = np.random.rand(A.shape[0], A.shape[1])
    B_redundant = np.random.rand(B.shape[0], B.shape[1])
    A_prime = np.hstack((A, A_redundant))
    B_prime = np.hstack((B, B_redundant))

    # 矩阵乘法
    C_prime = np.matmul(A_prime, B_prime)

    # 错误检测
    errors = np.where(C_prime != np.matmul(A, B))

    # 错误恢复
    for i, j in zip(errors[0],