MATLAB高斯拟合误差分析：评估拟合结果，保障准确性

# 1. MATLAB高斯拟合简介**

高斯拟合是一种非线性回归技术，用于拟合数据点到高斯函数。高斯函数是一个钟形曲线，由平均值、标准差和幅度三个参数定义。MATLAB提供了一个名为`fit`的函数，用于执行高斯拟合。

% 创建数据点
x = linspace(-5, 5, 100);
y = exp(-x.^2 / 2) + 0.1 * randn(size(x));

% 高斯拟合
model = fit(x', y', 'gauss1');

% 获取拟合参数
mu = model.b1;
sigma = model.c1;
A = model.a1;

通过高斯拟合，我们可以获得高斯函数的三个参数，用于描述数据的分布特征。

# 2. 高斯拟合误差分析理论

### 2.1 误差来源和分类

高斯拟合中存在的误差可以分为两大类：随机误差和系统误差。

**2.1.1 随机误差**

随机误差是不可预测的，由测量过程中的随机波动或噪声引起。这些误差通常符合正态分布，其大小和方向都是随机的。

**2.1.2 系统误差**

系统误差是可预测的，由测量设备或方法中的系统性偏差引起。这些误差通常是不对称的，并且会系统性地影响拟合结果。

### 2.2 误差评估指标

为了量化高斯拟合的误差，可以使用以下指标：

**2.2.1 均方根误差（RMSE）**

RMSE 是误差的平方和的平方根，表示了拟合曲线与实际数据的平均偏差。RMSE 越小，拟合精度越高。

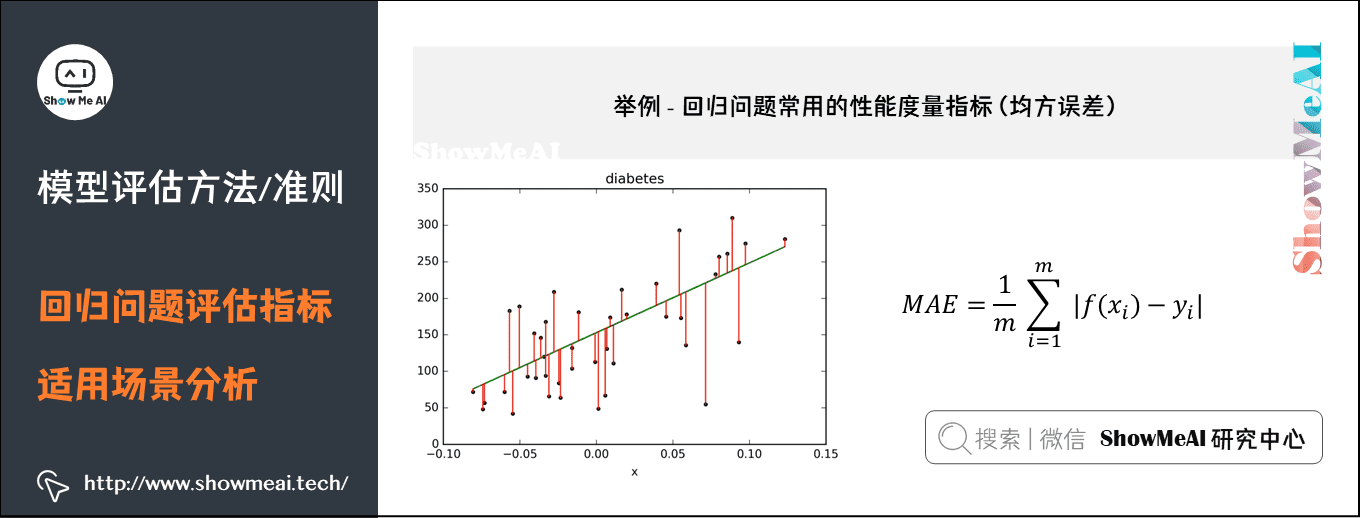
**2.2.2 最大绝对误差（MAE）**

MAE 是误差绝对值的平均值，表示了拟合曲线与实际数据之间最大的偏差。MAE 越小，拟合精度越高。

**2.2.3 相关系数（R^2）**

R^2 表示了拟合曲线与实际数据之间的相关程度。R^2 越接近 1，拟合精度越高。

# 3.1 数据预处理和模型选择

**3.1.1 数据清洗和转换**

在进行高斯拟合之前，数据预处理至关重要。它包括：

- **异常值检测和移除：**异常值会对拟合结果产生重大影响，因此需要识别并将其移除。
- **数据转换：**数据可能需要进行转换以符合高斯分布的假设。例如，对非正态分布的数据进行对数转换。
- **数据标准化：**数据标准化可以消除不同特征之间的量纲差异，从而提高拟合精度。

**3.1.2 不同模型的比较**

在选择高斯拟合模型时，需要考虑以下因素：

- **数据分布：**数据分布决定了最合适的模型类型，例如正态分布或对数正态分布。
- **模型复杂度：**模型复杂度与拟合精度之间存在权衡。较复杂的模型可能过度拟合数据，而较简单的模型可能无法捕捉数据的复杂性。
- **计算时间：**模型的计算时间也是一个需要考虑的因素，尤其是在处理大数据集时。

常见的模型选择方法包括：

- **Akaike信息准则（AIC）：**AIC衡量模型的拟合精度和复杂度之