MATLAB高斯拟合的最佳实践：分享经验和技巧，提升拟合水平

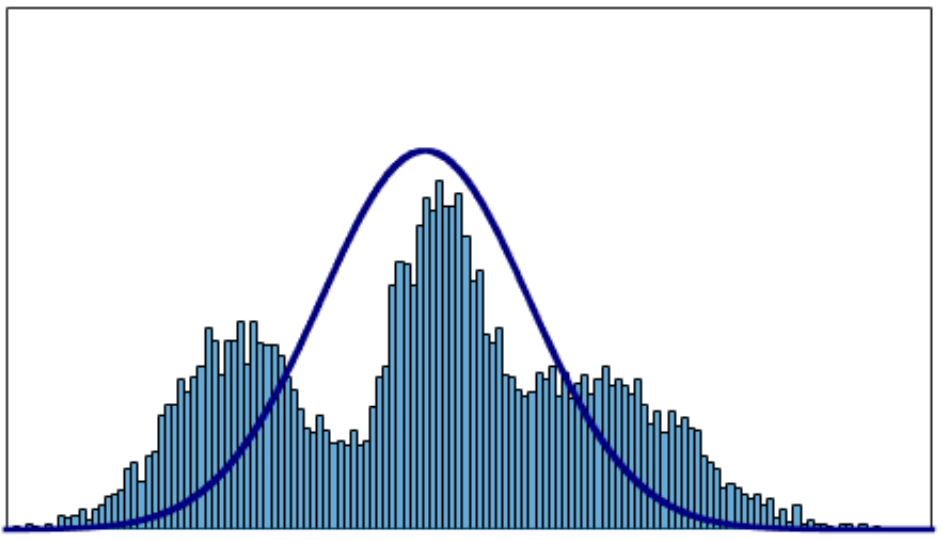
# 1. MATLAB高斯拟合概述**

高斯拟合是一种统计技术，用于拟合正态分布（也称为高斯分布）到给定的数据。它在各种应用中非常有用，包括数据分析、图像处理和科学计算。

MATLAB提供了一系列工具和函数，用于执行高斯拟合。本指南将介绍MATLAB高斯拟合的基础知识，包括理论基础、MATLAB实现和实践指南。通过遵循本指南，读者将能够有效地使用MATLAB进行高斯拟合，并解决各种实际问题。

# 2. 高斯拟合的理论基础

### 2.1 高斯分布的数学模型

高斯分布，也称为正态分布，是一种连续概率分布，其概率密度函数为：

f(x) = (1 / (σ√(2π))) * e^(-(x-μ)² / (2σ²))

其中：

* x 是随机变量
* μ 是均值
* σ 是标准差

高斯分布的钟形曲线是对称的，其峰值位于均值处。标准差表示分布的宽度，标准差越大，分布越平坦。

### 2.2 最小二乘法原理

最小二乘法是一种拟合算法，其目标是找到一组参数，使拟合曲线的误差平方和最小。对于高斯拟合，误差平方和定义为：

SSE = Σ(y_i - f(x_i))^2

其中：

* y_i 是观测值
* f(x_i) 是拟合曲线的预测值

最小二乘法算法通过迭代地调整参数，最小化 SSE。

### 2.3 拟合算法选择

有多种拟合算法可用于高斯拟合，包括：

* **Levenberg-Marquardt 算法：**一种非线性最小二乘算法，通常用于高斯拟合。
* **EM 算法：**一种期望最大化算法，可用于拟合混合高斯分布。
* **遗传算法：**一种启发式算法，可用于拟合复杂的高斯分布。

算法的选择取决于数据集和拟合要求。Levenberg-Marquardt 算法通常是高斯拟合的首选算法，因为它既准确又高效。

# 3. 高斯拟合的MATLAB实现**

### 3.1 内置函数fitgmdist

MATLAB提供了内置函数`fitgmdist`用于高斯混合模型的拟合。该函数使用期望最大化（EM）算法进行拟合，并返回一个`gmdistribution`对象，其中包含拟合模型的参数。

**代码块 1：使用fitgmdist拟合高斯混合模型**

% 生成模拟数据
data = [randn(100, 2) + [1, 1]; randn(100, 2) + [-1, -1]];

% 拟合高斯混合模型
model = fitgmdist(data, 2);

**逻辑分析：**

* `randn(100, 2)`生成100个服从标准正态分布的2D数据点。
* `[randn(100, 2) + [1, 1]; randn(100, 2) + [-1, -1]]`将数据分成两组，分别围绕（1, 1）和（-1, -1）分布。
* `fitgmdist(data, 2)`使用EM算法拟合一个具有2个分量的混合高斯模型。

**参数说明：**

* `data`：要拟合的数据，必须是2D或更高维度的矩阵。
* `2`：指定拟合模型的分量数。

### 3.2 自实现拟合算法

除了使用内置函数，还可以自己实现高斯拟合算法。一种常用的方法是使用最小二乘法，其中目标函数为：

f(μ, σ) = ∑(y_i - μ - σ^2 * x_i)^2

其中，`μ`和`σ`分别为高斯分布的均值和标准差。

**代码块 2：自实现高斯拟合算法**

% 定义目标函数
objective = @(params) s