Python中的L2正则化实战：如何轻松掌握岭回归

# 1. L2正则化和岭回归基础

在机器学习中，特别是在回归分析领域，L2正则化和岭回归是两种常用的技术，用于防止模型的过拟合并提高模型的泛化能力。本章将对L2正则化和岭回归进行基础介绍，并为后续章节的深入探讨奠定基础。

## 1.1 理解过拟合与正则化的必要性

在学习任何机器学习算法之前，了解模型的泛化与过拟合问题是至关重要的。过拟合是指模型在训练数据上表现得过于优秀，但在未见过的数据上表现不佳。其主要原因是模型过于复杂，以至于学习到了数据中的噪声而非潜在的真实模式。正则化技术因此被引入，旨在限制模型复杂度，防止过拟合。

## 1.2 L2正则化的简介

L2正则化，也称为岭回归（Ridge Regression）的一种形式，通过在损失函数中添加一个与权重的平方成正比的项来工作。其主要目标是减少模型的权重大小，鼓励模型在保持性能的同时，尽可能使用较小的权重值。L2正则化的引入，使得模型在面对多重共线性问题时，也能保持良好的稳定性和预测能力。

# 2. 理解L2正则化和岭回归的数学原理

## 2.1 L2正则化概念解析

### 2.1.1 过拟合与正则化的关系

在讨论L2正则化之前，理解过拟合现象对机器学习模型的影响至关重要。过拟合是指一个模型在训练数据上表现得非常好，但是一旦应用于新的、未见过的数据上时，其性能迅速下降。这通常是因为模型过于复杂，以至于它开始学习到训练数据中的噪声和异常值。

为了缓解过拟合问题，人们引入了正则化技术。正则化通过向损失函数中添加一个额外的惩罚项来对模型复杂度进行惩罚，从而抑制模型对于训练数据的过度拟合。L2正则化，也称为岭回归(Ridge Regression)，是正则化技术中的一种。

L2正则化在目标函数中引入了一个正则化项，通常是权重向量的L2范数（权重的平方和）乘以一个正则化参数λ。通过惩罚大权重值，L2正则化鼓励模型权重接近于零，但不是精确的零（这与L1正则化不同，后者倾向于产生稀疏权重）。这使得L2正则化不仅能够降低模型复杂度，同时保持模型的连续性和可导性，使得梯度下降等优化方法依然适用。

### 2.1.2 L2正则化的数学定义和目标函数

L2正则化的数学定义可以表述为最小化以下的目标函数：

其中，J(w)是原始的损失函数（如均方误差），λ是正则化参数，w是模型参数（权重向量）。λ的值越大，对权重的惩罚就越大，模型倾向于越简单。

直观理解，λ的作用是在模型的复杂度（由权重大小体现）和预测准确性之间进行权衡。如果λ取值过小，可能无法有效防止过拟合；而λ太大则可能导致欠拟合，即模型过于简单，无法捕捉数据中的关键特征。

## 2.2 岭回归的推导过程

### 2.2.1 最小二乘法回顾

在介绍岭回归之前，让我们先回顾一下最小二乘法，这是线性回归的基础。最小二乘法的核心思想是选择模型参数，使得预测值与实际值之间的误差的平方和最小。

给定一组数据点，我们的目标是找到一个线性方程 y = w*x + b，使得所有数据点到该线性方程的垂直距离（残差）的平方和最小。目标函数如下：

通过求导并令导数为零，我们可以找到w和b的最优解。

### 2.2.2 岭回归的目标函数和闭式解

在最小二乘法的基础上，我们引入L2正则化，即权重的平方和，并与原始的损失函数相乘，得到岭回归的目标函数：

其中，w是权重向量，y是真实值向量，X是特征矩阵，λ是正则化参数。

为了求解这个新的目标函数，我们对w进行求导，并令导数为零，可以得到w的闭式解（closed-form solution）。闭式解使得我们不需要迭代优化方法就可以直接计算出模型参数，极大地简化了计算过程。

在数学上，岭回归的闭式解可表示为：

这里，I是单位矩阵，α = λ + 1（有时调整为α = λ/n，n为样本数），X^T是X的转置矩阵，y是目标向量。当 λ = 0 时，岭回归的解退化为最小二乘法的解。

## 2.3 正则化参数λ的影响

### 2.3.1 λ值的确定方法

在使用岭回归时，确定合适的λ值是非常关键的。如果λ选择不当，可能会导致模型性能下降。确定λ的一个常用方法是交叉验证，尤其是k折交叉验证。在交叉验证中，数据被分成k个子集，其中k-1个子集用于训练，剩下的一个用于验证。这个过程重复k次，每次选择不同的子集作为验证集，最后对k次验证结果取平均。

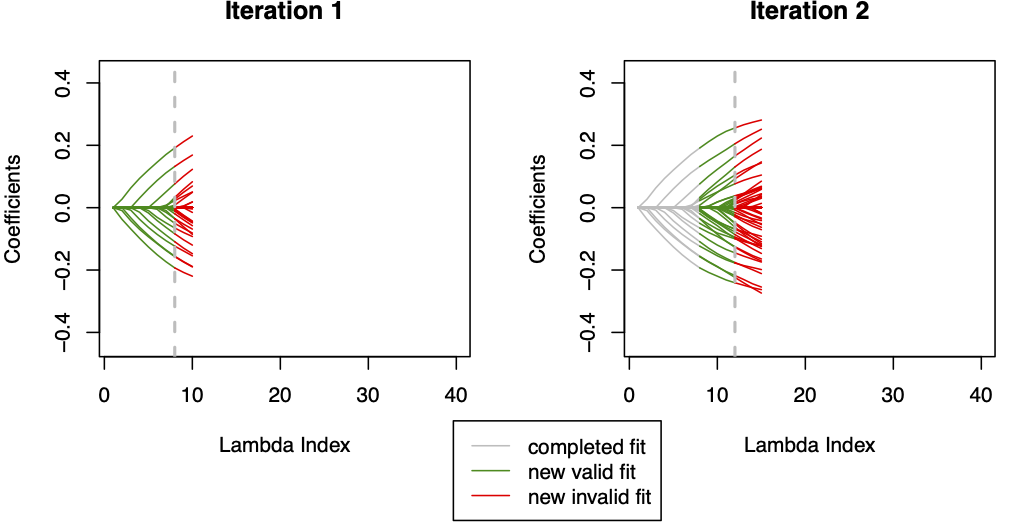
除了交叉验证之外，还有一些启发式方法可以帮助我们选择合适的λ值。例如，岭迹图是一种可视化工具，显示了不同λ值下各个回归系数的轨迹。通过观察岭迹图，我们可以判断哪些系数最先趋于零，从而帮助我们选择一个合理的λ值。

### 2.3.2 λ对模型复杂度和预测性能的影响

λ值的选择对于模型的复杂度和预测性能有着直接的影响。较大的λ值意味着更大的惩罚，导致权重的收缩，从而降低了模型的复杂度。在极端情况下，如果λ趋向于无穷大，所有的权重会趋向于零，模型的预测结果将只是一个常数（平均值），即模型退化为一个没有特征的基线模型。

另一方面，如果λ值太小，岭回归会退化成普通的最小二乘法，这样模型就有过拟合的风险。因此，选择合适的λ值是在模型复杂度和预测准确性之间进行权衡的关键步骤。在实际应用中，通过比较不同λ值下交叉验证的预测性能，我们可以确定一个相对平衡的λ值，以此构建一个既不过拟合也不欠拟合的模型。

通过以上章节的深入探讨，我们对L2正则化和岭回归的数学原理有了全面的理解。下一章，我们将介绍如何使用Python实现岭回归，进一步深化我们对这一主题的应用理解。

# 3. 使用Python实现岭回归

## 3.1 依赖库的安装和导入

### 3.1.1 安装NumPy和scikit-learn库

在开始使用Python实现岭回归之前，首先要确保已经安装了必要的科学计算和机器学习库。Python社区为我们提供了强大的库支持，特别是NumPy和scikit-learn，它们是数据分析和机器学习任务中不可或缺的工具。

NumPy是Python中用于科学计算的基础库，提供了高性能的多维数组对象和这些数组的操作工具。而scikit-learn是一个开源的机器学习库，它构建在NumPy、SciPy和matplotlib之上，集成了大量用于数据挖掘和数据分析的算法。

要安装这两个库，我们可以使用pip（Python的包安装程序）。打开命令行界面，输入以下命令即可进行安装：

pip install numpy scikit-learn

安装完成后，我们可以使用Python自带的`import`语句将这些库导入到我们的脚本中：

import numpy as np
import sklearn

### 3.1.2 导入必要的模块和函数

在编写岭回归的代码之前，我们需要导入一些必要的模块和函数。scikit-learn提供了专门的模块来处理线性回归，其中`Ridge`类就是用来实现岭回归的。我们还需要一些用于数据处理和模型评估的工具，比如`train_test_split`用于分割数据集，`cross_val_score`用于交叉验证，以及`mean_squared_error`用于计算均方误差。

在Python脚本中，我们可以这样导入：

from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_squared_error

以上步骤完成后，我们就准备好用Python来实现岭回归模型了。

## 3.2 岭回归模型的构建

### 3.2.1 从线性回归模型的限制讲起

在深入到具体的实现细节之前，我们先从线性回归模型的限制讲起。线性回归模型虽然是机器学习中非常基础的一个模型，但它的表达能力有限，特别是在处理具有多重共