【MATLAB陷波器设计性能评估】：测试与比较不同陷波器效果的专家指南


# 摘要
MATLAB作为一种强大的数学计算和信号处理软件，为设计和实现陷波器提供了灵活的工具。本文首先概述了陷波器的设计概念和理论基础，包括其定义、工作原理、分类、关键参数和数学模型。接着，深入探讨了在MATLAB环境下陷波器设计的实践方法，如使用内置函数、基于GUI的设计以及自定义算法的编程实现。文中还详细论述了陷波器性能评估的关键指标和测试方法，以及在信号去噪和多信号环境下的应用。最后，本文展望了适应性陷波器设计、新兴技术应用以及行业应用前景等未来趋势，并对设计中遇到的挑战提出了潜在解决方案。

# 关键字
MATLAB；陷波器设计；信号处理；性能评估；自适应算法；多信号环境

参考资源链接：[MATLAB实现70Hz陷波器设计与频谱分析](https://wenku.csdn.net/doc/6412b776be7fbd1778d4a63f?spm=1055.2635.3001.10343)
# 1. MATLAB陷波器设计概述

MATLAB，作为一款强大的数学计算和仿真软件，广泛应用于信号处理、控制系统和通信等领域。在这些应用中，陷波器设计显得尤为重要，因为它能有效地移除信号中的特定频率成分，抑制噪声或干扰。本章将简介MATLAB中的陷波器设计，为读者提供一个全面的概览。

首先，我们将探讨陷波器在信号处理中的角色及其设计重要性。我们还会讨论如何在MATLAB中应用陷波器进行信号处理，包括其设计方法、性能评估和实际应用案例。

其次，我们会从MATLAB的角度切入，通过具体案例展现如何在数字信号处理中实现陷波器设计。这将包括对MATLAB内置函数的使用说明、GUI设计步骤以及自定义算法的开发。这些内容将帮助读者掌握MATLAB环境下设计陷波器的基本方法。

总之，本章旨在为读者提供一个对MATLAB中陷波器设计的全面认识，为后续章节深入探讨理论基础、实践方法和应用案例打下坚实的基础。

# 2. 陷波器设计的理论基础

### 2.1 信号处理中的陷波器概念

#### 2.1.1 陷波器的定义和目的

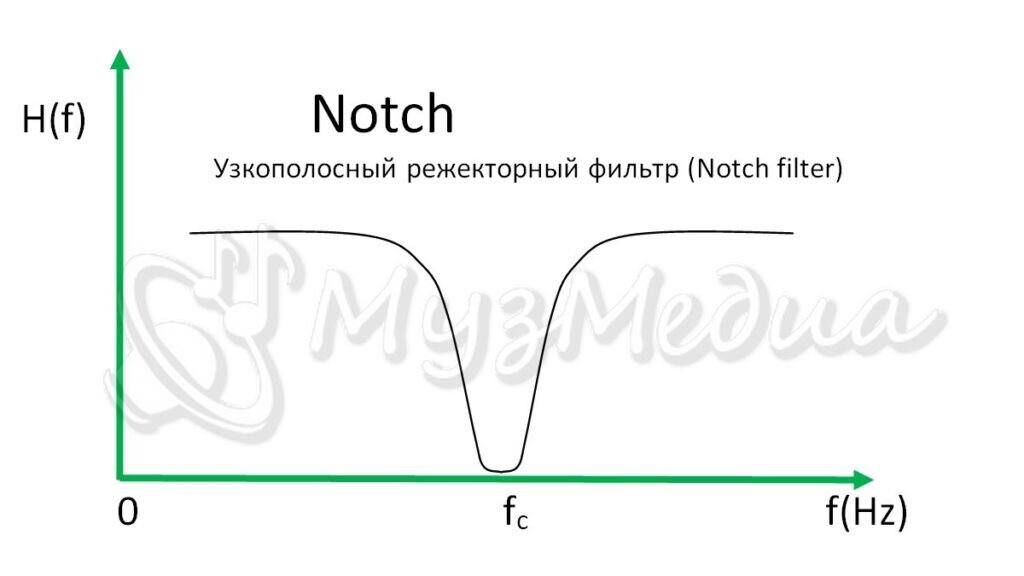
陷波器是一个在特定频段内能够显著减弱或消除信号的电子滤波器。它在信号处理中被广泛应用于抑制特定频率的干扰、消除信号中的噪声或消除信号中的固定频率成分。与一般的带通或带阻滤波器不同，陷波器通常设计得更为精细，以确保只影响非常狭窄的频率范围。在无线通信、音频处理、生物医学工程等领域，陷波器都发挥着至关重要的作用。

#### 2.1.2 陷波器的工作原理

从工作原理上讲，陷波器是通过调整其内部参数来实现对特定频率信号的抑制。在物理结构上，它通常由一系列电阻、电容和电感组成，通过这些元件的不同连接方式，可以构建不同特性的陷波器。在数字信号处理中，陷波器往往通过算法实现，如使用差分方程、Z变换和数字滤波器设计理论来模拟传统电子陷波器的功能。

### 2.2 陷波器的分类和特性

#### 2.2.1 按设计方法分类

根据设计方法的不同，陷波器主要可以分为模拟陷波器和数字陷波器两大类。模拟陷波器是在模拟域内直接通过电子组件实现，它适合于模拟信号的处理。数字陷波器则是通过数字信号处理算法来实现，适合于数字信号的处理。后者因为其灵活性和易于集成的特点，在现代信号处理中使用更加普遍。

#### 2.2.2 陷波器的关键参数和性能指标

陷波器的关键参数包括中心频率、陷波带宽、阻带衰减和通带纹波等。中心频率决定了陷波器抑制信号的频率点，陷波带宽决定了陷波器抑制信号的频率范围。阻带衰减表示信号在经过陷波器处理后，在中心频率处的衰减程度，而通带纹波则描述了通带内信号波动的幅度。这些性能指标是评价一个陷波器设计优劣的基准。

### 2.3 陷波器设计的基本数学模型

#### 2.3.1 滤波器设计理论

滤波器设计理论是研究如何通过数学模型来设计出满足特定性能指标的滤波器。这个理论包括了对滤波器类型（如低通、高通、带通、带阻和陷波器）的数学描述，以及如何通过算法设计出满足这些类型的滤波器。对于陷波器来说，关键在于如何精确控制其陷波频率和带宽。

#### 2.3.2 陷波器设计的数学公式和算法

陷波器的设计算法通常涉及到频率响应函数的设计，这包括了数学公式中的一些关键元素，如传递函数、极点、零点的配置。设计陷波器时，我们需要确保传递函数在陷波频率点有零点，同时在其两侧的通带内保持较高的增益。一个典型的陷波器设计算法如下所示：

% 设计陷波器的传递函数
% N为滤波器阶数
% wo为陷波频率
% bw为3dB带宽
[N, wo, bw] = buttord([wo-bw wo+bw], [wo-bw wo+bw], [1 1], [0 0], 's');
[b, a] = butter(N, [wo-bw wo+bw]/(wo*2), 'stop');

在上面的代码中，`buttord` 函数用于计算所需的滤波器阶数和3dB带宽，以确保在陷波频率处能够达到足够的阻带衰减。`butter` 函数则用于计算滤波器的系数。这些系数之后可以用于实现滤波器并应用于信号处理中。

这些基本的数学模型和算法构成了陷波器设计的理论基础，并指导着我们如何在MATLAB等软件中实现陷波器的设计。通过合理的设计和算法选择，我们可以针对不同的应用场景来优化陷波器的性能。在下一章中，我们将详细介绍如何在MATLAB环境中利用这些理论知识来设计和实现陷波器。

# 3. MATLAB中陷波器设计的实践方法

## 3.1 利用MATLAB内置函数设计陷波器
### 3.1.1 陷波器设计函数的使用

在MATLAB中设计陷波器的最基本和常用的方法之一是使用内置函数。这些函数为陷波器设计提供了丰富的接口，使设计过程既快速又高效。MATLAB提供了一整套用于设计数字滤波器的函数，包括`fdatool`、`designfilt`、`filter`等。其中`designfilt`函数提供了一种灵活的方式来设计具有特定参数的数字滤波器。

下面是使用`designfilt`函数设计一个陷波器的基本步骤：

1. 定义滤波器的采样频率以及陷波器的中心频率和带宽。
2. 使用`designfilt`函数创建一个数字陷波器设计对象。
3. 分析设计好的滤波器性能，包括频率响应和相位响应等。

下面是一个简单的示例代码，展示如何使用`designfilt`函数设计一个陷波器：

% 设定采样频率
Fs = 1000; % 以Hz为单位

% 设定陷波器的中心频率和带宽
f0 = 50; % 中心频率50Hz
bw = 10; % 带宽10Hz

% 设计陷波器
d = designfilt('notchiir', 'FilterOrder', 3, ...
               'HalfPowerFrequency1', f0-bw/2, ...
               'HalfPowerFrequency2', f0+bw/2, ...
               'SampleRate', Fs);

% 使用freqz函数分析陷波器的频率响应
freqz(d, 1024, Fs);

在这段代码中，`designfilt`函数用于创建一个三阶无限冲激响应（IIR）陷波器，其中心频率为50Hz，带宽为10Hz。`SampleRate`参数指定了采样频率为1000Hz。`freqz`函数用于绘制设计好的陷波器的频率响应。

### 3.1.2 设计案例分析

在设计陷波器时，需要考虑实际应用场景的需求，从而调整陷波器的参数来获得最佳性能。假设我们正在处理一个含有50Hz干扰的生物医学信号，并且希望消除这一特定频率的干扰。

我们使用上述代码作为起点，但可能需要对陷波器的参数进行调整。例如，如果干扰非常窄，我们需要减少陷波器的带宽；如果干扰影响范围很宽，则可能需要增加滤波器的阶数。

MATLAB允许我们方便地进行参数调整和性能评估。在设计过程中，可以使用`filter`函数来测试陷波器对真实信号的过滤效果。通过观察过滤前后信号的差异，可以对陷波器性能进行直观的评估。

% 加载生物医学信号数据
load('biosignal.mat'); % 假设信号变量名为'bioSignal'

% 使用设计好的陷波器过滤信号
filteredSignal = filter(d, bioSignal);

% 绘制原始信号和过滤后的信号对比
t = (0:length(bioSignal)-1)/Fs; % 创建时间向量
subplot(2,1,1);
plot(t, bioSignal);
title('原始信号');
xlabel('时间 (s)');
ylabel('幅度');

subplot(2,1,2);
plot(t, filteredSignal);
title('过滤后的信号');
xlabel('时间 (s)');
ylabel('幅度');

通过比较原始信号和过滤后的信号，我们可以评估陷波器是否成功地去除了特定频率的干扰。如果效果不理想，我们还可以调整陷波器的设计参数，如阶数、带宽，以及使用不同的设计方法来尝试改进性能。

## 3.2 基于图形用户界面的陷波器设计
### 3.2.1 GUI工具的介绍和应用

MATLAB的图