【MATLAB中陷波器的自适应调整】：动态干扰频率下的陷波器优化策略


# 摘要
本文系统地介绍了MATLAB中陷波器的概念、作用和设计基础理论，探讨了陷波器设计中的关键参数如中心频率、带宽、Q因子和陷波深度，以及传统设计方法，包括IIR和FIR滤波器设计、频率抽样和窗函数法。特别关注了动态干扰频率对陷波器性能的影响，并评估了在该条件下的陷波器性能局限性。文章进一步阐述了自适应陷波器的实现技术，包括自适应算法原理和在陷波器设计中的应用，同时对自适应陷波器的性能优化和资源消耗进行了探讨。在MATLAB环境下对自适应陷波器进行了模拟与分析，最后讨论了实际应用中的技术挑战和未来发展方向，特别强调了跨学科技术融合与智能化陷波器的趋势。

# 关键字
MATLAB；陷波器；设计参数；动态干扰频率；自适应算法；性能优化；模拟与分析

参考资源链接：[MATLAB实现70Hz陷波器设计与频谱分析](https://wenku.csdn.net/doc/6412b776be7fbd1778d4a63f?spm=1055.2635.3001.10343)
# 1. MATLAB中陷波器的概念和作用

## 1.1 陷波器简介
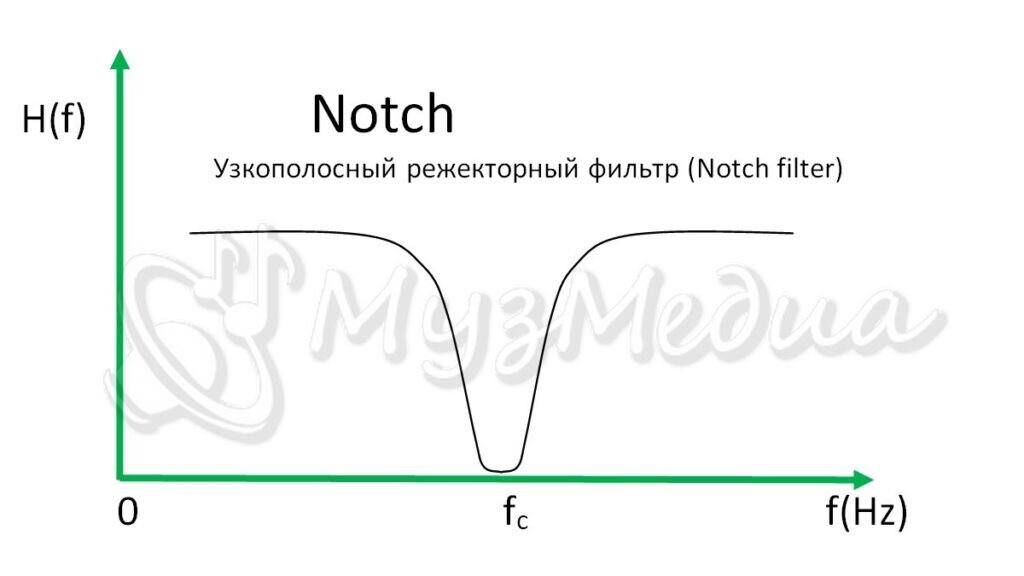
在信号处理中，陷波器（Notch Filter）是一种特殊的滤波器，用于在特定的频率点上衰减或消除信号中的干扰成分，而尽可能少影响其他频率成分。在MATLAB中，陷波器常用于音频处理、通信信号去噪等领域，以提高信号的清晰度和质量。

## 1.2 陷波器的应用场景
在多个应用场合中，如消除电源线的50/60Hz干扰、消除信号中的窄带噪声等，陷波器表现出强大的作用。它能够针对信号中的特定频率产生一个“陷坑”，通过设置适当的中心频率和陷波深度，可以有效地去除不需要的频率成分。

## 1.3 在MATLAB中使用陷波器的方法
要在MATLAB中使用陷波器，通常可以借助内置函数如 `iirnotch`、`fdatool` 等创建IIR滤波器。下面是一个基本的代码示例，用于创建一个中心频率为60Hz，带宽为5Hz的陷波器，并在一段信号上应用此滤波器。

% 设计一个中心频率为60Hz，带宽为5Hz的陷波器
Fs = 1000; % 采样频率
fc = 60; % 中心频率
bw = 5; % 带宽
notchFilter = iirnotch(fc/(Fs/2), bw/(Fs/2));

% 应用陷波器到含有60Hz干扰的信号上
t = 0:1/Fs:1; % 时间向量
x = sin(2*pi*fc*t) + 0.5*randn(size(t)); % 包含60Hz干扰的信号
y = filter(notchFilter, x); % 应用陷波器

% 绘制结果以对比效果
figure;
subplot(2,1,1);
plot(t, x);
title('Original Signal with 60Hz Interference');
xlabel('Time (s)');
ylabel('Amplitude');

subplot(2,1,2);
plot(t, y);
title('Signal after Notch Filtering');
xlabel('Time (s)');
ylabel('Amplitude');

此代码段首先定义了采样频率、中心频率和带宽，然后使用 `iirnotch` 函数生成了一个IIR陷波器，并将其应用到一个被60Hz信号干扰的测试信号上。最后绘制了原始信号和经过陷波器处理后的信号，以直观显示陷波器的效果。通过这段代码，我们可以深刻理解陷波器在MATLAB中的应用方法和效果。

# 2. 陷波器设计的基础理论

### 2.1 陷波器的基本工作原理
#### 2.1.1 陷波器的定义和功能
陷波器（Notch Filter）是一种用于削减或消除特定频率范围信号的电子滤波器。在通信、音频处理、信号采集等许多领域中，陷波器都能发挥关键作用。其功能体现在两个主要方面：一是能够有效去除信号中不需要的频率成分，比如电源线噪声（50Hz或60Hz）；二是保持信号中其他频率成分的完整性。

在数学上，陷波器可以通过频率响应函数来描述。理想的陷波器在特定频率点（或窄带）具有无限的衰减，而在其他频率带宽则保持信号不受影响。然而，实际应用中理想的陷波器是无法实现的，因此实际设计时需要对陷波器的性能指标进行权衡，包括通带和阻带的衰减量、过渡带宽度等。

#### 2.1.2 陷波器的数学模型
陷波器通常可以在频域中通过一个陷波函数来表示。对于一个理想的陷波器，其数学模型可以表达为：

\[ H(\omega) = \frac{1}{1 + k(\omega - \omega_0)^{2n}} \]

其中 \( H(\omega) \) 表示陷波器的频率响应，\( \omega \) 是角频率，\( \omega_0 \) 是要陷除的中心频率，\( k \) 是一个系数，而 \( n \) 是滤波器的阶数，决定了陷波的宽度和深度。

对于实际的数字实现，需要在时域中通过差分方程来实现上述频域响应。设计时一般需要考虑采样率、滤波器的稳定性和计算效率等因素。

### 2.2 陷波器设计的关键参数
#### 2.2.1 中心频率和带宽的确定
陷波器设计的首要任务是确定陷波的中心频率和带宽。中心频率决定了要滤除信号的频率点，而带宽则定义了陷波影响的频率范围。

- **中心频率**的确定通常依据干扰信号的特征频率，它直接影响了陷波器的抑制效果。在确定中心频率时需要考虑信号中干扰的实际频率，以及可能存在的频率漂移。
- **带宽**的选择则需要考虑两个因素：足够的带宽可以保证干扰信号被有效过滤，但带宽过宽又可能影响到相邻信号成分。带宽的计算往往需要依据陷波器设计的品质因数（Q因子）。

品质因数 \( Q \) 是描述滤波器选择性的一个参数，它是中心频率与陷波带宽的比值：

\[ Q = \frac{f_0}{B} \]

其中 \( f_0 \) 是中心频率，\( B \) 是带宽。Q值越大，陷波器的选择性越好，但其带宽也越窄，设计的复杂性也会增加。

#### 2.2.2 Q因子和陷波深度
Q因子是表征陷波器选择性的一个重要参数，它体现了陷波器在中心频率附近频率响应的尖锐程度。Q值越大，陷波器对信号的滤波效果越明显，但也意味着设计难度和计算开销的增加。

- **Q因子**的选择需要在滤波器的性能和资源消耗之间进行权衡。高Q因子意味着陷波器在中心频率附近具有较陡峭的滚降特性，对于紧邻的频率信号抑制效果更好。

- **陷波深度**定义了陷波器在中心频率处对信号的最小衰减值。通常陷波深度需要设计得足够大，以确保干扰信号被有效滤除。然而，深度越大，对滤波器的设计精度和稳定性要求就越高。

### 2.3 陷波器设计的传统方法
#### 2.3.1 IIR和FIR滤波器设计
陷波器通常可以通过无限脉冲响应（Infinite Impulse Response, IIR）和有限脉冲响应（Finite Impulse Response, FIR）滤波器来设计实现。

- **IIR滤波器**由于其递归结构，能够用较少的阶数获得较大的衰减效果，因此它们在陷波器设计中非常受欢迎。不过，IIR滤波器可能存在稳定性问题，并且在设计时需要