【MATLAB陷波器在音频信号处理中的应用】：音乐制作与语音识别的专家指南


# 摘要
本文系统介绍了MATLAB在音频信号处理中的陷波器应用，从基础理论到实际应用案例进行了全面分析。首先，介绍了音频信号的基本概念、信号处理的数学模型以及陷波器的原理与设计。随后，详细阐述了MATLAB在陷波器设计中的具体实现方法、性能评估及优化策略。本文还提供了陷波器在音频信号处理中的应用实践，包括音乐制作和语音识别中的噪声过滤，以及多通道和实时音频处理技术。最后，通过多个应用案例，评估了陷波器在不同场景中的表现，展望了陷波器技术及音频处理领域的未来趋势和技术挑战，探讨了其在创意产业和用户体验提升中的潜在应用前景。

# 关键字
MATLAB；陷波器设计；音频信号处理；性能评估；噪声过滤；实时音频处理

参考资源链接：[MATLAB实现70Hz陷波器设计与频谱分析](https://wenku.csdn.net/doc/6412b776be7fbd1778d4a63f?spm=1055.2635.3001.10343)
# 1. MATLAB陷波器基础介绍

在数字信号处理领域，MATLAB（Matrix Laboratory）是一款广泛使用的高性能语言，尤其在陷波器的设计和应用方面，它提供了一个强大的工具集。陷波器，又称为滤波器或带阻滤波器，主要用于在特定的频率范围内抑制或“陷落”信号。在音频信号处理中，陷波器可用于消除特定频率的干扰，如电源线的50或60 Hz的噪声，或是去除音频文件中的回声和杂音。

## 1.1 陷波器的数学基础

首先，了解陷波器的数学基础，需要从离散傅里叶变换（DFT）开始。DFT是数字信号处理中分析频率成分的关键数学工具。通过将时域信号转换为频域表示，我们可以识别并过滤掉不需要的频率成分。陷波器设计中常用的数学模型包括无限脉冲响应（IIR）和有限脉冲响应（FIR）滤波器设计方法。

## 1.2 陷波器在MATLAB中的实现

在MATLAB中，实现陷波器通常涉及到内置函数，如`filter`和`fft`等。例如，使用`filter`函数可以实现一个简单的IIR陷波器，其设计往往依赖于`butter`、`cheby1`、`cheby2`等函数来生成滤波器的系数。这些函数的参数包括滤波器的阶数和截止频率等，通过这些参数的合理设置，可以设计出符合特定需求的陷波器。

一个简单的IIR陷波器示例代码如下：

% 设计一个陷波器来抑制50Hz的噪声（假设采样频率为500Hz）
Fs = 500; % 采样频率
F0 = 50; % 需要抑制的噪声频率
Q = 20; % 品质因子，影响陷波带宽
[b, a] = iirnotch(F0/(Fs/2), Q); % 设计陷波器系数
x = randn(1, 1000); % 生成测试信号
y = filter(b, a, x); % 应用陷波器

上述代码中，`iirnotch`函数用于生成陷波器的系数，这些系数随后被`filter`函数用来对输入信号`x`进行处理。输出信号`y`即为经过陷波器处理后的信号。通过这段代码，我们可以直观地看到如何在MATLAB中设计并使用陷波器。

在接下去的章节中，我们将深入探讨陷波器的设计原理，以及如何在不同的音频处理场景中应用MATLAB进行陷波器的优化与性能评估。

# 2. ```
# 第二章：音频信号处理理论
音频信号处理作为现代信息技术的重要组成部分，它的发展极大地推动了通信、广播、音乐制作、语音识别等多个行业的进步。深入理解音频信号处理的理论基础，对于设计有效的陷波器至关重要。本章节将详细探讨音频信号的基本概念、信号处理的数学模型以及陷波器的原理与设计。

## 2.1 音频信号的基本概念
音频信号是指频率范围在20Hz至20kHz之间，人们能够感知的声波信号。这一范围内的声波能够通过空气等介质传播，并被人类的听觉系统接收。

### 2.1.1 音频信号的特性与分类
音频信号具有多个特性，如频率、振幅、相位和时长等。根据音频信号的特性，可以将其分为连续信号和离散信号。连续信号是指在时间上连续的信号，而离散信号则是指时间上不连续的信号。

音频信号通常可以分为单声道和立体声。单声道信号只有一个声音通道，而立体声信号则包含两个声道，可以提供更丰富的听觉体验。此外，音频信号还根据编码方式分为模拟音频信号和数字音频信号。

### 2.1.2 音频信号的数字化与采样率
音频信号的数字化涉及到将模拟音频信号转换为数字信号的过程，这是通过模数转换器（ADC）完成的。数字化后的音频信号由一系列离散的数值表示，这些数值可以在计算机系统中进行处理。

采样率是音频数字化过程中的一个关键参数，它指的是每秒采样的次数，单位是赫兹（Hz）。根据奈奎斯特定理，为了精确重建一个模拟信号，采样率应至少为信号最高频率的两倍。在实践中，常用的CD质量音频采样率为44.1kHz，而广播质量的采样率通常为48kHz。

## 2.2 信号处理的数学模型
信号处理的数学模型为分析和处理音频信号提供了强有力的工具。其中，时域分析和频域分析是信号处理中最基本的方法。

### 2.2.1 时域与频域分析基础
时域分析主要关注信号随时间的变化。通过时域分析，我们可以了解到信号的波形、周期性和趋势等信息。常用的时域分析工具包括波形图、自相关函数和互相关函数。

频域分析则是将信号从时间域转换到频率域，通过这种转换可以得到信号的频率组成和频率分布。傅里叶变换是实现时域到频域转换的核心数学工具。快速傅里叶变换（FFT）作为一种高效的傅里叶变换算法，在数字信号处理中得到了广泛应用。

### 2.2.2 傅里叶变换及其在信号处理中的应用
傅里叶变换能够将复杂的信号分解为一系列简单的正弦波，每个正弦波对应一个频率分量。这对于分析音频信号至关重要，因为不同的频率分量可能代表了不同的声音源。

在信号处理中，傅里叶变换的应用非常广泛。它可以用于信号的滤波、压缩编码、频率分析和信号合成。例如，通过频域滤波，我们可以移除音频信号中不需要的频率成分，也就是噪声。

## 2.3 陷波器的原理与设计
陷波器是一种特殊类型的滤波器，用于在频谱中消除特定频率成分，其工作原理与设计方法是音频信号处理的核心内容。

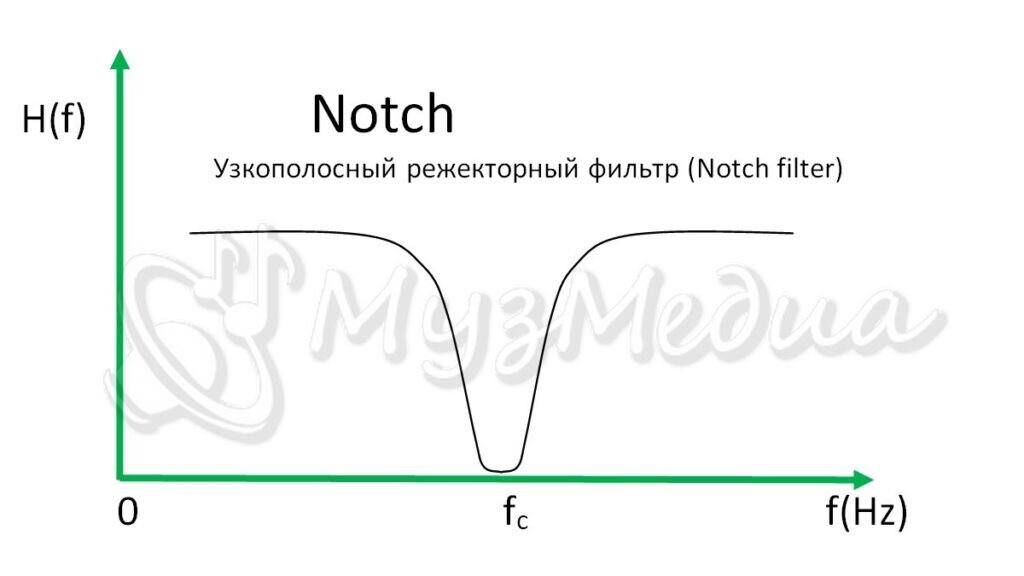
### 2.3.1 陷波器的定义和作用
陷波器（Notch Filter）是一种带阻滤波器，它的设计目的是在特定的频率范围内极大地减少信号的幅度。在音频信号处理中，陷波器通常用于消除音频信号中的干扰或杂音，如50Hz或60Hz的电源干扰，以及消除乐器或声源的某些特定谐波。

### 2.3.2 常见的陷波器设计方法
常见的陷波器设计方法包括巴特沃斯陷波器、切比雪夫陷波器和椭圆陷波器。巴特沃斯陷波器在通带和阻带之间具有平滑的过渡，而切比雪夫陷波器在通带或阻带中具有更快的衰减速度。椭圆陷波器则在通带和阻带中都有较快的衰减速度，但其设计相对复杂。

设计陷波器时需要确定陷波的中心频率、带宽和陷波深度。中心频率决定了需要消除的频率成分，带宽决定了陷波器作用的频率范围，而陷波深度则指定了陷波器在中心频率处减少信号幅度的程度。

通过本章节的介绍，我们已经对音频信号处理理论有了初步的了解。下一章节我们将深入探讨MATLAB在陷波器设计中的具体应用。

# 3. MATLAB在陷波器设计中的应用

在音频信号处理领域，陷波器设计是一个重要的环节，尤其是在去除噪声、改善信号质量方面。MATLAB作为一款功能强大的数学计算和工程仿真软件，在设计和实现陷波器方面显示出了极高的效率和便捷性。本章将深入探讨MATLAB在陷波器设计中的具体应用，涵盖工具箱的使用、代码实现、性能评估与优化等多个方面。

## 3.1 MATLAB信号处理工具箱

### 3.1.1 工具箱中的关键函数介绍

MATLAB信号处理工具箱为用户提供了大量用于信号分析和处理的函数，极大地简化了算法的实现和