Lua堆数据结构实践：优先队列与堆排序的深入解析

# 1. 堆数据结构基础

## 1.1 堆数据结构概述

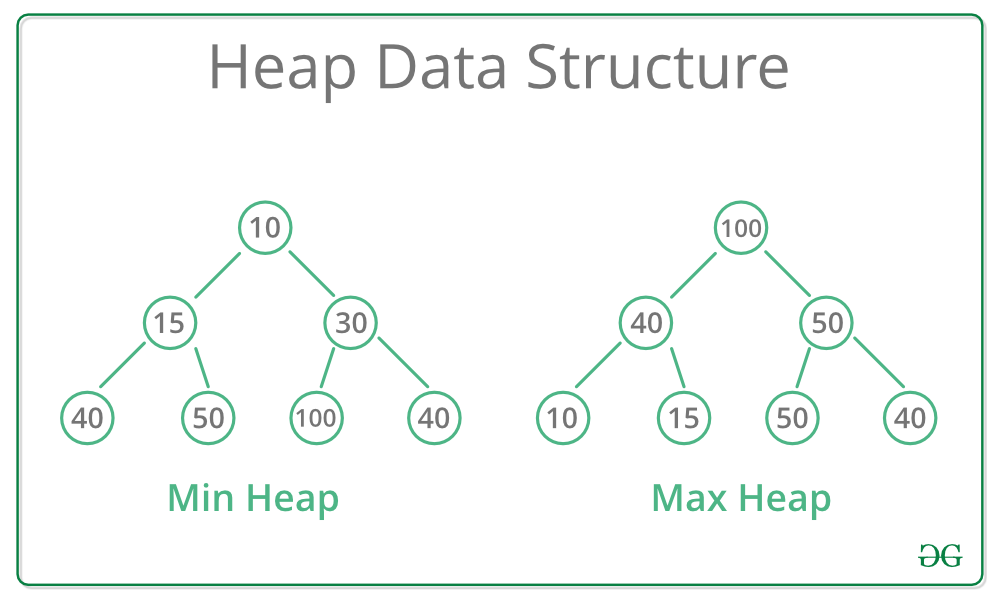
堆是一种特殊的完全二叉树，通常用数组或链表实现。在堆中，每个节点的值都大于或等于其子节点的值（称为最大堆），或者每个节点的值都小于或等于其子节点的值（称为最小堆）。堆结构常用于实现优先队列、堆排序等算法。

## 1.2 堆的基本操作

堆的主要操作包括插入（insert）、删除最小/最大元素（deleteMin/deleteMax）和调整堆（heapify）。插入操作通常将新元素添加到堆的末尾，并向上调整以满足堆的性质。删除操作则是移除堆顶元素，然后将堆尾元素放到堆顶，并向下调整。

## 1.3 堆与优先队列的关系

堆是实现优先队列的一种有效数据结构。优先队列按照元素的优先级进行出队操作，堆的性质正好可以保证最高优先级的元素总是位于队列的前端。在实际应用中，堆结构能够以对数时间复杂度完成优先级的调整和元素的检索。

# 2. Lua中的优先队列实现

### 2.1 优先队列的数据结构和操作

#### 2.1.1 优先队列的概念与应用场景

优先队列是一种特殊的队列，在这种队列中，每个元素都有一个优先级属性。在优先队列中，元素的删除操作是按照优先级顺序进行的，而不是按照入队的顺序。因此，具有最高优先级的元素总是位于队列的前端。

这种数据结构在多种应用场合下非常有用。例如，在事件驱动的模拟中，事件可以按照发生的紧急程度排队；在计算机网络中，用于调度不同优先级的数据包传输；在任务调度中，用于安排高优先级任务的执行顺序。

#### 2.1.2 优先队列的关键操作：插入与删除

在优先队列的实现中，两个关键的操作是插入和删除。插入操作用于添加新元素到队列中，而删除操作用于移除并返回队列中优先级最高的元素。

- 插入操作：通常，新元素插入到优先队列的末尾，然后通过一些步骤调整，直到它处于正确的位置（即符合优先级顺序）。
- 删除操作：总是移除优先级最高的元素（通常是队列的头部元素），并返回它。如果优先队列是通过最小堆实现的，那么最小元素将在顶部，反之亦然。

### 2.2 Lua优先队列的代码实现

#### 2.2.1 使用数组构建优先队列

在Lua中，我们可以使用数组来构建优先队列。以下是使用数组实现优先队列的一个基本示例：

function PriorityQueue()
    self.heap = {}  -- 初始化数组作为堆
    self.count = 0  -- 记录当前元素的数量
end

function PriorityQueue:insert(value, priority)
    table.insert(self.heap, {value, priority})  -- 插入元素
    self.count = self.count + 1
    self:_percolateUp(self.count)  -- 调整元素位置以满足优先级顺序
end

function PriorityQueue:remove()
    local top = self.heap[1]
    self.heap[1] = self.heap[self.count]  -- 将最后一个元素放到顶部
    self.count = self.count - 1
    self.heap[self.count + 1] = nil  -- 移除最后一个元素
    self:_percolateDown(1)  -- 调整新顶部元素的位置以满足优先级顺序
    return top[1]
end

function PriorityQueue:_percolateUp(index)
    local element = self.heap[index]
    while index > 1 do
        local parentIndex = math.floor(index / 2)
        local parent = self.heap[parentIndex]
        if parent[2] <= element[2] then break end  -- 如果父节点优先级更高或相同，则停止
        self.heap[index], self.heap[parentIndex] = self.heap[parentIndex], self.heap[index]  -- 交换位置
        index = parentIndex
    end
end

function PriorityQueue:_percolateDown(index)
    local element = self.heap[index]
    local count = self.count
    while (2 * index) <= count do
        local childIndex = 2 * index
        local swapChild = childIndex
        local child = self.heap[childIndex]
        local right = childIndex + 1
        if right <= count and self.heap[right][2] < child[2] then
            swapChild = right
            child = self.heap[right]
        end
        if child[2] >= element[2] then break end  -- 如果子节点优先级更低，则停止
        self.heap[index], self.heap[swapChild] = self.heap[swapChild], self.heap[index]  -- 交换位置
        index = swapChild
    end
end

该代码实现了插入和删除操作，还包含私有方法`_percolateUp`和`_percolateDown`用于调整堆的结构。

### 2.3 Lua优先队列的性能分析

#### 2.3.1 时间复杂度分析

- **插入操作**：最坏情况下，每次插入需要O(log n)时间。因为新元素可能需要一路向堆的顶部进行堆化（heapify），直到根节点。
- **删除操作**：删除最大/最小元素的时间复杂度也是O(log n)，因为需要从根节点开始向下堆化。

#### 2.3.2 空间复杂度分析

优先队列的空间复杂度与存储元素的数量直接相关，为O(n)，其中n是队列中元素的数量。这是因为我们需要一个数组来存储队列的所有元素。

在下一章节，我们将深入探讨堆排序算法以及如何在Lua中实现。

# 3. Lua中的堆排序算法