Lua高级数据结构探索：红黑树与B树的实现原理

# 1. 高级数据结构在Lua中的重要性

在编程领域，数据结构是组织和存储数据的基石。它们不仅影响代码的可读性和维护性，还直接决定了软件的性能。高级数据结构，如红黑树和B树，提供了在各种应用中高效处理数据的途径。在Lua这种轻量级脚本语言中，合理利用这些高级数据结构，可以大幅提升数据操作的效率和系统的响应速度。

Lua语言由于其简洁性和灵活性，常被用于嵌入到应用程序中提供脚本能力。当Lua用于数据密集型任务时，就需要高效的数据结构来支撑。红黑树和B树的运用，可以优化数据的存储和检索，这对于需要频繁进行增删改查操作的应用尤其重要。本章将探讨这些高级数据结构在Lua中的应用重要性和潜在价值。通过理解它们的特性及其在Lua中的实现，开发者可以更好地构建复杂的数据处理逻辑，实现高效的应用程序设计。

# 2. 红黑树的理论基础与实现

### 2.1 红黑树的理论基础
#### 2.1.1 二叉搜索树的基本概念
二叉搜索树（Binary Search Tree，简称BST）是一种特殊的二叉树，它满足以下性质：对于树中的任意节点X，它的左子树上所有节点的值都小于X的值，它的右子树上所有节点的值都大于X的值。这样的性质保证了二叉搜索树在进行查找操作时，可以利用二分查找的思想，从而具有较高的效率。然而，普通的二叉搜索树在面对有序或逆序插入的数据时，会退化成链表，导致其性能从O(log n)下降到O(n)。

#### 2.1.2 红黑树的性质定义
红黑树是在二叉搜索树基础上增加了一些额外的规则，以确保树不会退化成链表，从而在最坏情况下也能保持较好的性能。红黑树的性质包括：
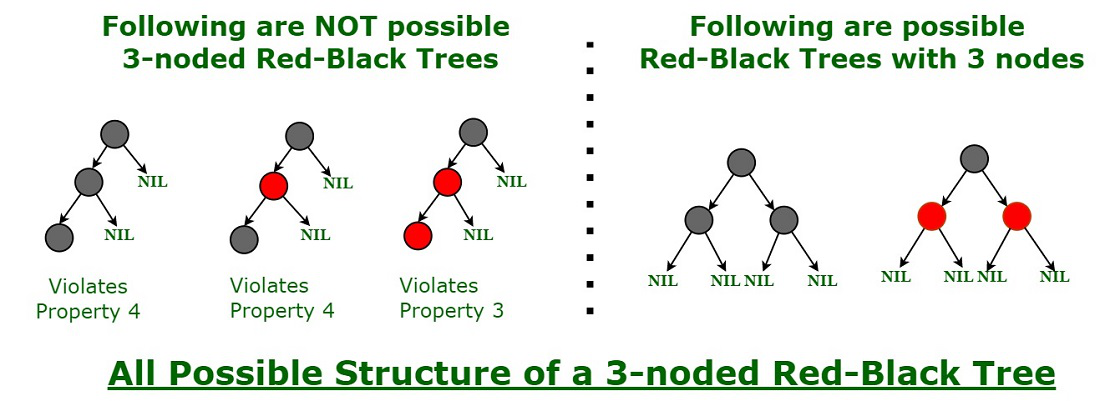
1. 每个节点要么是红色，要么是黑色。
2. 根节点是黑色。
3. 所有叶子节点（NIL节点，空节点）都是黑色。
4. 每个红色节点的两个子节点都是黑色（从每个叶子到根的所有路径上不能有两个连续的红色节点）。
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

通过这些性质，红黑树确保了最长的路径不会超过最短的路径的两倍，因而其基本操作（插入、删除、查找）的时间复杂度均为O(log n)。

### 2.2 红黑树的插入操作
#### 2.2.1 基本插入流程
插入操作是红黑树中较为复杂的过程。首先，按照二叉搜索树的规则找到插入位置，创建一个红色节点。然后，将其插入到树中。由于红黑树性质的限制，插入可能导致树的不平衡。因此，接下来需要通过一系列的颜色变换和树的旋转来恢复红黑树的性质。

#### 2.2.2 插入后的颜色调整与树平衡
插入后可能会出现以下情况，破坏了红黑树的性质，需要进行调整：
- 双重红色冲突：新插入的节点和其父节点都是红色。
- 黑色冲突：从新节点出发，有路径上的黑色节点数发生变化。

解决这些冲突通常涉及以下操作：
- 变色：将某个节点的颜色从红色变为黑色，或从黑色变为红色。
- 左旋和右旋：树旋转是调整树结构的常用方法，分为左旋和右旋。

下面给出一个红黑树插入操作的伪代码示例：

function insert(self, key)
    local node = Node(key)
    node.color = 'red'
    local parent = nil
    local current = self.root

    while current ~= nil do
        parent = current
        if node.key < current.key then
            current = current.left
        else
            current = current.right
        end
    end

    node.parent = parent
    if parent == nil then
        self.root = node
    elseif node.key < parent.key then
        parent.left = node
    else
        parent.right = node
    end

    if node.parent == nil then
        node.color = 'black'
        return
    end

    if node.parent.parent == nil then
        return
    end

    self.fix_insert(node)
end

在这个示例中，`fix_insert` 函数将负责插入后的树调整过程。

### 2.3 红黑树的删除操作
#### 2.3.1 基本删除流程
红黑树的删除操作比插入操作更为复杂，因为在删除节点后，树可能会违反红黑树的性质。首先，删除操作可以分为几种情况：删除红色节点、删除黑色节点、用红色节点替换黑色节点等。在删除节点时，如果删除的是黑色节点，需要通过调整来保证黑色平衡。具体来说，可以通过“借调”或“颜色翻转”等手段来处理。

#### 2.3.2 删除后的颜色调整与树平衡
删除节点可能导致树中黑色节点的数量减少，破坏了红黑树的第五个性质。为了恢复平衡，可能需要以下调整步骤：
- 重新着色：通过改变某些节点的颜色来重新平衡黑色节点的数量。
- 树旋转：与插入操作类似，通过旋转来调整树结构。

伪代码如下：

function delete(self, key)
    local node = self.search(key)
    if node == nil then
        return
    end

    if node.left == nil or node.right == nil then
        local child = node.left or node.right
        if child ~= nil then
            child.parent = node.parent
        end
        if node.parent == nil then
            self.root = child
        elseif node == node.parent.left then
            node.parent.left = child
        else
            node.parent.right = child
        end
        if node.color == 'black' then
            self.fix_delete(child)
        end
    else
        local successor = self.minimum(node.right)
        node.key, successor.key = successor.key, node.key
        node = successor
        if node.right ~= nil then
            node.right.parent = node.parent
        end
        if node.parent == nil then
            self.root = node.right
        elseif node ==