Lua算法实战精讲：动态规划与贪心算法案例解析

# 1. Lua编程基础回顾

## 1.1 Lua语言简介
Lua是一种轻量级的脚本语言，因其简洁高效的特性和灵活的扩展性，在游戏开发、嵌入式系统及网络应用中得到了广泛应用。它被设计为嵌入到应用程序中，提供灵活的扩展和定制功能。

## 1.2 Lua基本语法
Lua的基本语法包括变量声明、控制结构、函数定义等。变量在Lua中无需显式声明类型，支持局部变量和全局变量。控制结构如if-else、for循环和while循环用于控制程序流程。

--Lua中的变量声明和函数定义示例
function add(a, b)
    return a + b
end

local sum = add(10, 20)
print(sum)  -- 输出30

## 1.3 表（Table）的使用
在Lua中，表是一种构建复杂数据结构的基本工具，既可以当作数组也可以当作字典使用。通过表可以实现高级的数据组织和操作。

--Lua中表的定义和使用示例
local points = {}
points[1] = {x = 10, y = 20}
points[2] = {x = 20, y = 30}

for i, v in ipairs(points) do
    print(i, v.x, v.y)
end

## 1.4 模块和包管理
Lua支持模块化编程，允许开发者将代码分割成可重用的模块。使用`require`函数可以加载和使用这些模块，大大增强了代码的模块化和重用性。

--Lua模块化示例
-- 文件mathlib.lua
local M = {}
function M.add(x, y) return x + y end
return M

-- 主程序
local mathlib = require("mathlib")
print(mathlib.add(10, 20))  -- 输出30

总结：Lua作为一门高效灵活的脚本语言，其简洁的语法、强大的表结构和模块化编程特性非常适合用于算法开发和性能优化。掌握Lua的基础知识对于深入学习动态规划和贪心算法等高级编程技巧至关重要。

# 2. 动态规划的理论基础

### 动态规划的概念和原理

动态规划（Dynamic Programming，DP）是一种算法思想，它将复杂问题分解成简单的子问题，通过解决子问题来逐步解决问题的方法。动态规划的核心在于将已解决的子问题答案存储起来，以便后续直接利用，避免重复计算，从而提高效率。

动态规划可以解决许多优化问题，尤其是那些存在重叠子问题和最优子结构特性的问题。重叠子问题是指在递归过程中，相同的子问题会被多次求解；最优子结构是指一个问题的最优解包含其子问题的最优解。典型的动态规划问题包括Fibonacci数列、背包问题、最短路径问题等。

### 状态转移方程的构建方法

构建动态规划的解决方案，核心在于构建状态转移方程。状态转移方程是一个数学描述，它定义了不同状态之间的转换关系，以及在转换过程中如何计算目标函数（比如求最大值或最小值）。

以下是一些构建状态转移方程的常见步骤：

1. 定义状态：明确表示问题状态的变量，通常是变量的数组或矩阵形式。
2. 确定初始条件：确定问题最简单情况的解，即递归的最底层。
3. 状态转移方程：根据子问题之间的关系，推导出从已知子问题解到当前问题解的转换规则。
4. 计算顺序：确定状态计算的顺序，以确保所有需要的子问题在计算当前状态之前已经被解决。

### 动态规划经典案例分析

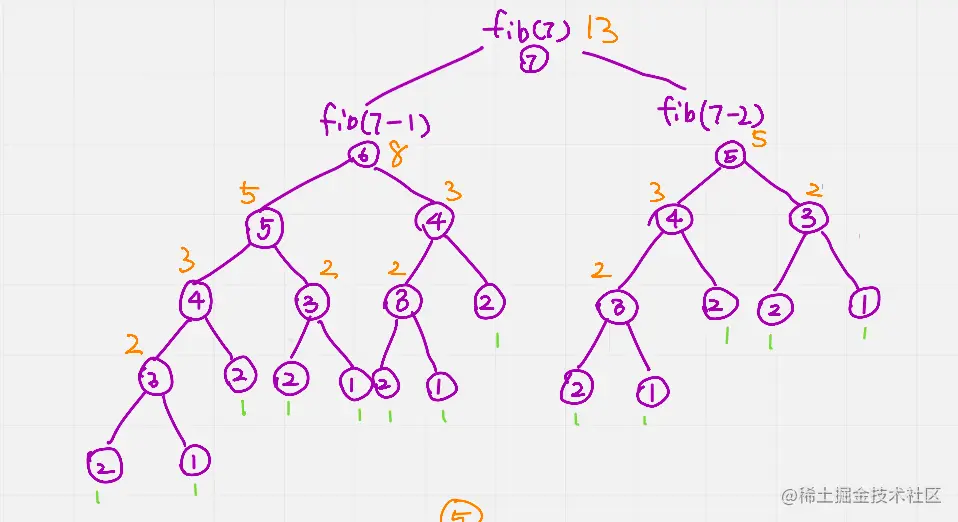
#### Fibonacci数列问题

Fibonacci数列是一个经典的动态规划问题。数列中每个数字是前两个数字的和，定义如下：

F(0) = 0, F(1) = 1
F(n) = F(n-1) + F(n-2), for n > 1

使用动态规划方法，我们可以构建如下状态转移方程：

dp[i] = dp[i-1] + dp[i-2], for i > 1

其中，`dp[i]`表示Fibonacci数列的第`i`项。初始条件是`dp[0] = 0`和`dp[1] = 1`。

下面是使用Lua实现的Fibonacci数列计算：

function fibonacci(n)
    if n <= 0 then return 0 end
    if n == 1 then return 1 end

    local dp = {}
    dp[1], dp[2] = 1, 1
    for i = 3, n do
        dp[i] = dp[i-1] + dp[i-2]
    end
    return dp[n]
end

print(fibonacci(10))  -- 输出34

#### 0-1背包问题

0-1背包问题是指给定一组物品，每种物品都有自己的重量和价值，在限定的总重量内，选择其中一部分物品，使得这部分物品的总价值最大。

问题可以定义为：

- `w[i]`表示第`i`个物品的重量
- `v[i]`表示第`i`个物品的价值
- `W`表示背包的总容量

状态转移方程为：

dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i]), if j >= w[i]
dp[i][j] = dp[i-1][j], otherwise

其中`dp[i][j]`表示在前`i`个物品中选择总重量不超过`j`的最大价值。

### 动态规划问题的Lua实现

#### 递归与记忆化搜索的Lua实现

递归是动态规划的一种自然实现方式，但可能因重复计算而导致效率低下。记忆化搜索是在递归的基础上，将已经计算过的子问题结果存储起来，当遇到相同子问题时直接返回结果，从而避免重复计算。

下面是0-1背包问题的递归实现，使用Lua的表来模拟记忆化搜索：

function knapsack01的记忆化搜索(w, v, W, n)
    local memo = {}
    local function dp(i, j)
        if i == 0 or j == 0 then return 0 end
        if memo[i][j] ~= nil then return memo[i][j] end

        if w[i] > j then
            memo[i][j] = dp(i-1, j)
        else
            memo[i][j] = math.max(dp(i-1, j), dp(i-1, j-w[i]) + v[i])
        end
        return memo[i][j]
    end

    return dp(n, W)
end

-- 示例数据
local w = {1, 2, 4, 2, 5}
local v = {5, 3, 5, 3, 2}
local W = 10
local n = #w

print(knapsack01(w, v, W, n))  -- 输出14

#### 迭代法与表格法的Lua实现

迭代法通常比递归更加高效，它使用表格或数组逐步构建最终解决方案。这种表格法适用于解决状态转移方程，因为它以自底向上的方式填表，不会出现重复计算。

以下是0-1背包问题的迭代实现：

function knapsack01迭代法(w, v, W, n)
    local dp = {}
    for i = 0, n do
        dp[i] = {}
    end

    for i = 0, n do
        for j = 0, W do
            if i == 0 or j == 0 then
                dp[i][j] = 0
            elseif w[i] > j then
                dp[i][j] = dp[i-1][j]
            else
                dp[i][j] = math.max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])
            end
        end
    end

    return dp[n][W]
end

print(knapsack01迭代法(w, v, W, n))  -- 输出14

通过上述实现，我们可以看到动态规划在解决优化问题时的强大能力。无论是递归、记忆化搜索还是迭代法，每种方法都有其适用的场景和优势。在实际应用中，开发者应根据问题的特性和需求选择合适的动态规划实现方式。

# 3. 贪心算法理论与实践

## 3.1 贪心算法的理论基础

### 3.1.1 贪心算法的概念和原理

贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。它并不保证会得到最优解，但是在某些问题中，贪心算法会得到最优解。

贪心算法的原理可以用一句话来概括：“在对问题求解时，总是做出在当前看来是最好的选择”。也就是说，不从整体最优考虑，它所做的选择只是在某种意义上的局部最优。

### 3.1.2 贪心选择性质和最优子结构

贪心选择性质意味着通过局部最优选择，来产生全局最优解。然而，并不是所有具有贪心选择性质的问题都存在最优子结构性质，但具有最优子结构性质的问题，可以考虑使用贪心算法。

最优子结构性质是指一个问题的最优解包含其子问题的最优解。也就是说，一个问题的最优解可以通过它的子问题的最优解来构造。

## 3.2 贪心算法的经典案例分析

### 3.2.1 最小生成树问题

在图论中，最小生成树是一个非常典型的贪心算法应用案例。它的目标是在加权连通图中找到一个边的子集，使得这些边构成的树包含图中的所有顶点，并且边的权值之和尽可能小。

### 3.2.2 单源最短路径问题

单源最短路径问题中，贪心算法也可以发挥其威力。Dijkstra算法是一个典型的贪心算法，用于在带权图中找到从单一源点到其他所有顶点的最短路径。

### 3.2.3 贪心算法在区间调度中的应用

区间调度问题是一个常见的贪心算法问题，比如假设有一个需要使用资源的活动集合，每个活动都指定了一个开始时间、结束时间和占用资源的持续时间。目标是安排尽可能多的活动，以便它们不会彼此冲突。

## 3.3 贪心算法问题的Lua实现

### 3.3.1 基于贪心策略的Lua编码实现

以最小生成树问题为例，我们可以使用Kruskal算法或者Prim算法来实现。以下是使用Kruskal算法的一个简单Lua代码示例：

function find(parent, i)
    if parent[i] == -1 then
        return i
    else
        return find(parent, parent[i])
    end
end

function union(parent, rank, x, y)
    xroot = find(parent, x)
    yroot = find(parent, y)
    if rank[xroot] < rank[yroot] then
        parent[xroot] = yroot
    else
        parent[yroot] = xroot
        if rank[xroot] == rank[yroot] then
            rank[xroot] = rank[xroot] + 1
        end
    end
end

function kruskal(graph)
    local result = {} -- this will store the final output
    local i = 0
    local e = 0
    -- step 1: Sort all the edges in non-decreasing order of their weight
    table.sort(graph)
    local parent = {}
    local rank = {}
    -- Create V subsets with single elements
    for node = 1, #graph[1] do
        parent[node] = -1
        rank[node] = 0
    end
    while e < #graph[1] - 1 do
        -- step 2: Pick the smallest edge. And increment the index for next iteration
        i = i + 1
        local u, v, w = table.unpack(graph[i])
        u = find(parent, u)
        v = find(parent, v)
        -- If including this edge does't cause cycle, then include it in result
        -- and do a union of two sets.
        if u ~= v then
            e = e + 1
            result[e] = {u, v, w}
            union(parent, rank, u, v)
        end
    end
    -- return the constructed MST
    return result
end

-- Example usage:
local graph = {
    {1, 2, 10},
    {1, 3, 20},
    {2, 4, 30},
    {3, 4, 40},
    {2, 3, 15}
}

local mst = kruskal(graph)
for i, edge in ipairs(mst) do
    print(string.format("Edge %d:(%d, %d) Weight: %d", i, edge[1], edge[2], edge[3]))
end

### 3.3.2 贪心算法与动态规划的对比分析

贪心算法与动态规划两者之间的对比是一个非常有趣的议题。贪心算法在每一步选择中都采取当前最优解，而动态规划则考虑了整个问题的最优解。动态规划通常需要存储中间结果并使用这些结果来解决问题，而贪心算法不一定需要存储所有中间结果。

在贪心算法中，每一步的决策仅仅依赖于当前可用的信息，不需要考虑整个问题的历史信息。但在动态规划中，每一步的决策都依赖于以前的决策历史。因此，贪心算法的时间复杂度通常比动态规划低，因为不需要存储和回溯大量的中间状态。

Lua中实现这两种算法的时候，我们通常会使用表格来存储动态规划的中间结果，而贪心算法则往往只需要维持有限的几个变量。例如，在Kruskal算法中，我们只需要维持`parent`和`rank`数组来避免循环的产生，而不需要记录所有可能的状态。

通过这个简单的例子，我们可以看到贪心算法和动态规划在解决问题时的差异，以及它们在不同场景下的应用和限制。理解这些差异对于选择合适算法来解决实际问题至关重要。

# 4. 算法优化与效率提升

## 4.1 算法的时间复杂度分析

### 4.1.1 大O表示法和常见复杂度分析

大O表示法是算法分析中用来描述算法性能的一种方式，它提供了一种量度算法执行时间或空间需求的方法，与问题规模 n 的关系密切。大O表示法关注的是增长趋势，而不是具体的值。

例如，对于一个简单的循环遍历算法，如果循环执行 n 次，那么该算法的时间复杂度为 O(n)。如果存在两个嵌套循环，每个循环遍历 n 次，那么时间复杂度为 O(n^2)。

常见的时间复杂度类型有：

- **O(1)**：常数时间复杂度，表示算法的执行时间不随输入规模 n 的增加而增加。
- **O(log n)**：对数时间复杂度，典型的例子是二分查找。
- **O(n)**：线性时间复杂度，表示算法的执行时间与输入规模 n 成正比。
- **O(n log n)**：线性对数时间复杂度，常见于分治算法。
- **O(n^2)**：平方时间复杂度，常见于简单的双重循环算法。
- **O(2^n)**：指数时间复杂度，算法的时间随输入规模 n 指数级增长。

理解这些基本的时间复杂度类型对于算法效率的评估和比较至关重要。

### 4.1.2 算法优化的常见策略

算法优化的目标是提高算法的时间效率和空间效率。常见策略包括但不限于：

- **减少不必要的计算**：避免重复计算，可以使用记忆化搜索或者动态规划。
- **选择合适的算法或数据结构**：例如，使用哈希表来快速查找，使用平衡树来维护有序序列。
- **避免递归栈开销**：递归算法简单易懂，但可能导致栈空间的浪费。在可能的情况下，考虑使用迭代算法替代。
- **使用原地算法