揭秘图的遍历算法：DFS与BFS的原理与应用，助你轻松解决图论难题

# 1. 图的遍历算法概述**

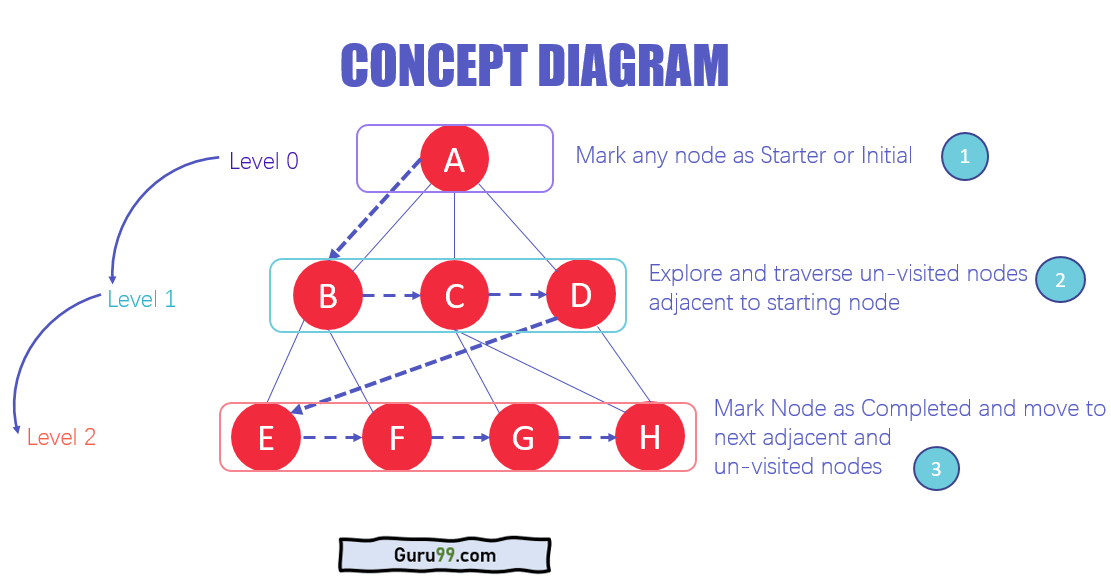
图的遍历算法是一种系统地访问图中所有节点和边的技术。它在计算机科学中广泛应用，用于解决各种问题，如连通性检测、路径查找和图着色。图的遍历算法主要分为两大类：深度优先搜索（DFS）和广度优先搜索（BFS）。

DFS 采用递归或栈的方式，从一个起始节点开始，沿着一条路径深度探索，直到遇到死胡同。BFS 则采用队列的方式，从一个起始节点开始，逐层扩展，直到访问所有节点。

# 2. 深度优先搜索（DFS）**

**2.1 DFS 的原理和实现**

深度优先搜索（DFS）是一种图遍历算法，它沿着图的深度进行遍历，即从一个节点出发，沿着一条路径一直遍历到不能再深入为止，然后再回溯到上一个节点，继续遍历另一条路径。

DFS 的实现通常使用递归或栈数据结构。递归的实现方式如下：

def dfs(graph, start_node):
    visited.add(start_node)
    for neighbor in graph[start_node]:
        if neighbor not in visited:
            dfs(graph, neighbor)

栈的实现方式如下：

def dfs(graph, start_node):
    stack = [start_node]
    while stack:
        current_node = stack.pop()
        visited.add(current_node)
        for neighbor in graph[current_node]:
            if neighbor not in visited:
                stack.append(neighbor)

**2.2 DFS 的应用场景**

DFS 算法在图遍历中有着广泛的应用，常见场景包括：

**2.2.1 连通性检测**

DFS 可以用来检测图中是否存在连通分量。连通分量是指图中一群互相连接的节点，从其中任何一个节点出发都可以到达其他节点。DFS 从一个节点出发，遍历所有与之相连的节点，并标记为已访问。如果遍历完成后，图中所有节点都被标记为已访问，则图是连通的。

**2.2.2 环检测**

DFS 还可以用来检测图中是否存在环。环是指图中的一条路径，从一个节点出发，经过多个节点，最后又回到出发节点。DFS 在遍历过程中，如果遇到一个节点已经被访问过，则说明图中存在环。

**代码示例：**

# 连通性检测
def is_connected(graph):
    visited = set()
    dfs(graph, 0)  # 从节点 0 开始遍历
    return len(visited) == len(graph)  # 判断所有节点是否都被访问

# 环检测
def has_cycle(graph):
    visited = set()
    stack = set()
    for node in graph:
        if node not in visited:
            if dfs_cycle(graph, node, visited, stack):
                return True
    return False

def dfs_cycle(graph, node, visited, stack):
    visited.add(node)
    stack.add(node)
    for neighbor in graph[node]:
        if neighbor not in visited:
            if dfs_cycle(graph, neighbor, visited, stack):
                return True
        elif neighbor in stack:
            return True
    stack.remove(node)
    return False

# 3. 广度优先搜索（BFS）

### 3.1 BFS 的原理和实现

广度优先搜索（BFS）是一种图遍历算法，它按照图中节点的层级进行遍历，先遍历当前节点的所有相邻节点，再遍历相邻节点的所有相邻节点，以此类推。

BFS 的实现通常使用队列数据结构。算法从起始节点开始，将其入队。然后，依次出队队列中的节点，并将其所有未访问的相邻节点入队。重复此过程，直到队列为空。

def bfs(graph, start):
    """
    广度优先搜索算法

    参数：
    graph：图的邻接表表示
    start：起始节点

    返回：
    visited：访问过的节点列表
    """

    visited = set()
    queue = [start]

    while queue:
        node = queue.pop(0)  # 出队
        if node not in visited:
            visited.add(node)
            for neighbor in graph[node]:
                if neighbor not in visited:
                    queue.append(neighbor)  # 入队

    return visited

### 3.2 BFS 的应用场景

BFS 算法在图论中有着广泛的应用，以下是一些常见的应用场景：

#### 3.2.1 最短路径问题

BFS 可以用来求解图中两点之间的最短路径。算法从起始点开始，逐层遍历图，直到找到目标点。由于 BFS 按照层级遍历，因此找到的目标点一定是最短路径。

#### 3.2.2 最小生成树

BFS 还可以用来求解图的最小生成树。最小生成树是一棵包含图中所有节点，且边权和最小的树。BFS 可以通过不断添加边权最小的边来构造最小生成树。

### 3.2.3 连通性检测

BFS 可以用来检测图是否连通。如果图中存在一个连通分量，则从任意节点开始 BFS 遍历，都可以访问到图中的所有节点。否则，图中存在多个连通分量。

### 3.2.4 环检测

BFS 可以用来检测图中是否存在环。如果图中存在环，则从任意节点开始 BFS 遍历，一定会在某个时刻访问到已经访问过的节点，从而检测到环的存在。

### 3.2.5 其他应用

BFS 算法还可以在其他领域中得到应用，例如：

- 网络路由
- 社交网络中的社群发现
- 棋盘游戏的求解
- 计算机视觉中的图像分割

# 4. DFS 与 BFS 的比较和选择

### 4.1 算法复杂度对比

DFS 和 BFS 算法的复杂度主要取决于图的规模和遍历方式。

**DFS**

* **时间复杂度：**O(V + E)，其中 V 是图中顶点的数量，E 是边的数量。
* **空间复杂度：**O(V)，因为 DFS 使用栈来存储已访问的顶点。

**BFS**

* **时间复杂度：**O(V + E)，与 DFS 相同。
* **空间复杂度：**O(V)，因为 BFS 使用队列来存储已访问的顶点。

### 4.2 适用场景分析

DFS 和 BFS 算法在不同的场景下具有不同的优势：

**DFS**

* **适合场景：**
* 检测图的连通性
* 检测图中是否存在环
* 查找图中的回路
* **不适合场景：**
* 寻找最短路径
* 寻找最小生成树

**BFS**

* **适合场景：**
* 寻找最短路径
* 寻找最小生成树
* 检测图中是否存在连通分量
* **不适合场景：**
* 检测图中是否存在环
* 查找图中的回路

### 4.3 实际应用案例

**案例 1：连通性检测**

def dfs_connectivity(graph, start_node):
    """
    使用 DFS 检测图的连通性

    参数：
        graph: 图的邻接表表示
        start_node: 开始遍历的顶点

    返回：
        连通的顶点集合
    """
    visited = set()  # 已访问的顶点集合
    stack = [start_node]  # 栈

    while stack:
        node = stack.pop()
        if node not in visited:
            visited.add(node)
            for neighbor in graph[node]:
                if neighbor not in visited:
                    stack.append(neighbor)

    return visited

**案例 2：最短路径查找**

def bfs_shortest_path(graph, source_node, target_node):
    """
    使用 BFS 查找图中两个顶点之间的最短路径

    参数：
        graph: 图的邻接表表示
        source_node: 起始顶点
        target_node: 目标顶点

    返回：
        最短路径的顶点序列
    """
    queue = [(source_node, [source_node])]  # 队列，存储顶点及其路径
    visited = set()  # 已访问的顶点集合

    while queue:
        node, path = queue.pop(0)
        if node == target_node:
            return path
        if node not in visited:
            visited.add(node)
            for neighbor in graph[node]:
                if neighbor not in visited:
                    queue.append((neighbor, path + [neighbor]))

    return None

# 5. 图的遍历算法在实际应用中的拓展

图的遍历算法在实际应用中有着广泛的拓展，以下是一些常见的应用场景：

### 5.1 图论算法在网络中的应用

#### 5.1.1 路由算法

路由算法是网络中用于确定数据包从源节点到目标节点最佳路径的算法。图论算法可以用来构建网络拓扑图，其中节点表示网络设备，边表示连接它们的链路。路由算法使用图的遍历算法来找到从源节点到目标节点的最短路径或最优路径。

#### 5.1.2 流量控制

流量控制是网络中用于管理和优化数据流的机制。图论算法可以用来构建网络拓扑图，并使用图的遍历算法来分析网络流量模式。这有助于识别网络瓶颈并优化流量路由，以提高网络性能。

### 5.2 图论算法在社交网络中的应用

#### 5.2.1 社群发现

社群发现是社交网络中用于识别具有相似特征或兴趣的用户群体的过程。图论算法可以用来构建社交网络图，其中节点表示用户，边表示用户之间的连接。社群发现算法使用图的遍历算法来识别网络中的社群。

#### 5.2.2 关系推荐

关系推荐是社交网络中用于为用户推荐潜在朋友或联系人的过程。图论算法可以用来构建社交网络图，并使用图的遍历算法来查找与给定用户具有相似连接或兴趣的用户。关系推荐算法使用这些信息来为用户推荐潜在的连接。