【模型参数学习曲线】：如何分析与提升模型性能

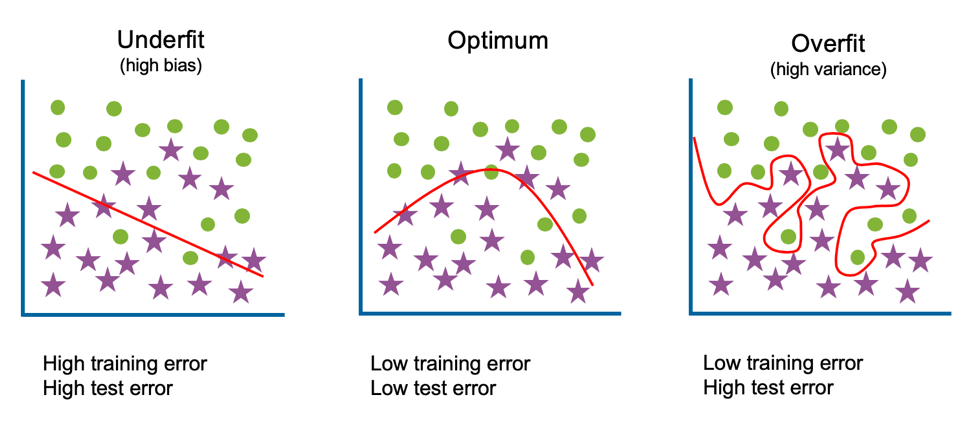
# 1. 模型参数学习曲线概述

在机器学习和深度学习的实践中，了解模型参数学习曲线是至关重要的。学习曲线是一种可视化技术，它展示了模型性能与训练数据量之间关系的图形。通过观察学习曲线，我们能够识别模型是否过拟合或欠拟合，以及是否需要更多的数据或模型调整。学习曲线通常包含两个主要部分：训练误差和验证误差。理想的学习曲线是随着训练数据的增加，训练和验证误差都会下降，直到达到一个稳定点。学习曲线分析不仅可以帮助我们选择正确的模型结构，还可以指导我们优化训练过程。本章将引导读者深入理解学习曲线，并提供基础概念，为后续章节的性能指标、优化方法和调优策略打下坚实的基础。

# 2. 理解模型性能指标

## 2.1 基本性能指标

模型性能指标是衡量机器学习模型优劣的关键，它们帮助我们评估模型在特定任务上的表现。为了深入理解这些指标，我们将从准确率、召回率和F1分数开始，逐步探讨混淆矩阵与ROC曲线等更为详细的概念。

### 2.1.1 准确率、召回率和F1分数

在二分类问题中，模型的预测结果常常通过几个关键指标来衡量，其中最基础的包括准确率（Accuracy）、召回率（Recall）和F1分数（F1 Score）。

- **准确率（Accuracy）** 衡量模型预测正确的样本占总样本的比例。公式为：

\[ \text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN} \]

其中，TP（True Positive）表示模型正确识别的正样本数，TN（True Negative）表示模型正确识别的负样本数，FP（False Positive）表示模型错误地识别为正的负样本数，FN（False Negative）表示模型错误地识别为负的正样本数。

- **召回率（Recall）** 又称真正率（True Positive Rate），它关注的是模型识别出的正样本数占实际正样本总数的比例。公式为：

\[ \text{Recall} = \frac{TP}{TP + FN} \]

- **F1分数** 是准确率和召回率的调和平均数，适用于平衡准确率和召回率的情况。F1分数的计算公式为：

\[ F1 = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} \]

其中，Precision（精确率）表示模型识别为正的样本中实际为正的样本所占的比例。

一般来说，准确率和召回率之间存在一定的权衡关系，高准确率可能意味着低召回率，反之亦然。F1分数作为两者之间的平衡，是综合评估模型性能的一个有效指标。

### 2.1.2 混淆矩阵与ROC曲线

为了更细致地评估模型的性能，我们通常会使用混淆矩阵（Confusion Matrix）和接收者操作特征曲线（Receiver Operating Characteristic Curve，简称ROC曲线）。

- **混淆矩阵** 是一个表格，用于描述分类模型的性能。它不仅显示了模型预测正确的样本数（对角线上的TP和TN），也直观展示了模型的错误分类情况（非对角线上的FP和FN）。一个典型的混淆矩阵如下所示：

| 预测\实际 | 正类 | 负类 |
|-----------|-------|-------|
| 正类 | TP | FP |
| 负类 | FN | TN |

- **ROC曲线** 是一个二维平面上的曲线，其横轴是假正率（FPR，也称为1 - 特异性），纵轴是真正率（TPR，即召回率）。ROC曲线下面积（Area Under Curve，简称AUC）可以反映分类器的性能。理想的分类器具有AUC值为1，而随机分类器的AUC值为0.5。

下图为ROC曲线的示例：

在实际应用中，我们会根据不同的需求选择适合的性能指标。例如，在医疗诊断等场景中，召回率往往比准确率更为重要，因为漏诊的代价远高于误诊。

## 2.2 损失函数与优化

性能指标帮助我们评价模型的预测结果，而损失函数和优化算法则是在训练过程中指导模型学习的主要工具。

### 2.2.1 损失函数的作用和选择

损失函数（Loss Function）用来衡量模型的预测值与实际值之间的差异，是模型优化的核心部分。在训练过程中，模型会尝试最小化损失函数来提升预测的准确性。

常见的损失函数包括：

- **均方误差（MSE）** 用于回归问题，衡量模型预测值与真实值之间差的平方的平均值。
\[ MSE = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2 \]

- **交叉熵损失（Cross-Entropy Loss）** 常用于分类问题，衡量预测概率分布与真实概率分布之间的差异。
\[ CrossEntropy = -\sum_{i=1}^{N} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right] \]

损失函数的选择取决于具体的任务和模型类型。例如，在深度学习的多分类任务中，交叉熵损失几乎是标准选择。

### 2.2.2 优化算法的基本原理

优化算法用来更新模型的参数以最小化损失函数。常用的优化算法包括：

- **梯度下降（Gradient Descent）** 是一种迭代优化算法，通过计算损失函数关于模型参数的梯度来更新参数。参数的更新公式为：

\[ \theta_{\text{new}} = \theta_{\text{old}} - \alpha \cdot \nabla_\theta L(\theta) \]

其中，\( \theta \) 表示模型参数，\( L(\theta) \) 是损失函数，\( \nabla_\theta L(\theta) \) 表示梯度，\( \alpha \) 是学习率。

- **随机梯度下降（Stochastic Gradient Descent，简称SGD）** 是梯度下降的一种变体，它在每次迭代中使用一个样本来计算梯度，从而减少计算量。

- **Adam优化器** 结合了Momentum和RMSprop两种优化算法的优点，使用梯度的一阶矩估计和二阶矩估计来调整学习率。

优化算法的选择和参数配置对模型的性能有显著影响。例如，学习率过高可能会导致模型在最小值附近震荡，过低则可能导致训练过程缓慢收敛。

## 2.3 性能评估方法

在模型训练完毕后，需要通过一定的评估方法来检验模型的泛化能力。交叉验证和过拟合检测是评估模型泛化能力的常用方法。

### 2.3.1 交叉验证与过拟合检测

- **交叉验证（Cross-Validation）** 是一种模型评估技术，它能更充分地使用有限的数据进行训练和验证。最常用的交叉验证方法是k折交叉验证，它将数据集分为k个大小相似的互斥子集，然后将每个子集轮流作为验证集，其余作为训练集。这样每个子集都用于验证一次，共进行k次训练和验证，最后取k次结果的平均值作为评估指标。

下面是一个简单地k折交叉验证的伪代码：

  from sklearn.model_selection import KFold
  from sklearn.metrics import accuracy_score
  from sklearn.base import clone
  X, y = load_data()
  kfold = KFold(n_splits=5)
  scores = []

  for train_index, test_index in kfold.split(X):
      X_train, X_test = X[train_index], X[test_index]
      y_train, y_test = y[train_index], y[test_index]