【数据结构应用】：图的存储技术在网络算法中的创新应用

# 1. 图的理论基础与存储技术概述

在计算机科学领域中，图是表达实体间关系的一种强大工具。图由一系列顶点（或节点）以及连接它们的边组成，可以抽象地表示各种关系网络，如社交网络、网络通信、数据库系统等。本章将从基础理论入手，探讨图的数学概念和存储技术的基本原理。通过理论的铺垫和实际存储技术的介绍，旨在为读者提供对图处理的全面理解，为后续章节中图算法的优化和应用打下坚实的基础。

# 2. 图的基本存储方法及其实现

## 2.1 邻接矩阵存储法

### 2.1.1 邻接矩阵存储法的原理和特点

邻接矩阵是一种用二维数组来表示图的存储方法，对于图G=(V, E)，其中V是顶点的集合，E是边的集合。在邻接矩阵存储法中，创建一个n*n的矩阵A，其中n是顶点的数量。矩阵中的元素A[i][j]表示顶点i和顶点j之间是否相连，如果相连则A[i][j]为1，否则为0。

邻接矩阵存储法的特点包括：
- **空间效率**：对于无权图而言，邻接矩阵需要存储n*n个元素，如果图是稠密的，即大部分顶点都彼此相连，那么邻接矩阵的空间效率是可接受的。
- **查找效率**：查找两个顶点之间是否存在边，时间复杂度是O(1)，这是因为可以直接通过索引访问矩阵元素。
- **对称性**：无向图的邻接矩阵是对称的，因为无向图中的边是双向的。
- **适合表示带权图**：对于有权图，邻接矩阵可以存储边的权重信息，而不是简单的连接状态。

### 2.1.2 邻接矩阵存储法的算法实现

邻接矩阵的算法实现一般包括图的初始化、添加边、删除边和查询边等操作。以下是一个使用Python实现的邻接矩阵存储法的示例代码：

class AdjacencyMatrixGraph:
    def __init__(self, size):
        self.matrix = [[0] * size for _ in range(size)]

    def add_edge(self, v1, v2):
        self.matrix[v1][v2] = 1
        self.matrix[v2][v1] = 1  # 如果是无向图，需要对称添加

    def remove_edge(self, v1, v2):
        self.matrix[v1][v2] = 0
        self.matrix[v2][v1] = 0  # 如果是无向图，需要对称删除

    def has_edge(self, v1, v2):
        return self.matrix[v1][v2] != 0

# 示例使用
graph = AdjacencyMatrixGraph(5)
graph.add_edge(0, 1)
print(graph.has_edge(0, 1))  # 输出: True
graph.remove_edge(0, 1)
print(graph.has_edge(0, 1))  # 输出: False

在这个实现中，我们创建了一个`AdjacencyMatrixGraph`类，它有一个二维数组`matrix`来存储邻接矩阵，以及四个方法：`__init__`来初始化图，`add_edge`来添加边，`remove_edge`来删除边，和`has_edge`来检查两个顶点之间是否存在边。

## 2.2 邻接表存储法

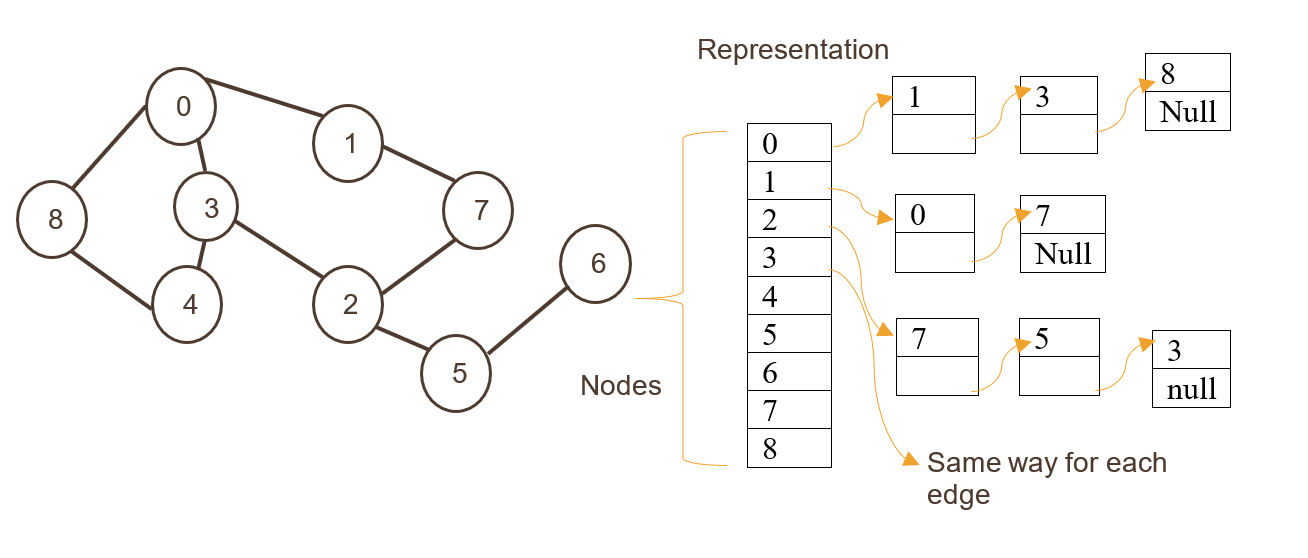
### 2.2.1 邻接表存储法的原理和特点

与邻接矩阵不同，邻接表是一种更加节省空间的图的存储方法。它使用链表或者数组来存储与每个顶点相邻的所有顶点。邻接表由n个列表组成，每个列表对应图中的一个顶点。每个列表中的元素是一个节点，节点包含两个信息：一个是与该顶点相邻的顶点信息，另一个是链到下一个相邻顶点的指针或索引。

邻接表存储法的特点包括：
- **空间效率**：相比邻接矩阵，对于稀疏图而言，邻接表可以节省大量空间，因为它仅存储实际存在的边的信息。
- **动态性**：邻接表易于添加和删除顶点和边，因为不需要移动多个元素。
- **复杂度**：遍历所有边的时间复杂度为O(|V| + |E|)，其中|V|是顶点数，|E|是边数。

### 2.2.2 邻接表存储法的算法实现

邻接表的实现可以采用多种数据结构，例如使用字典或哈希表来存储图，其中键为顶点，值为与该顶点相邻的顶点列表。以下是使用Python字典实现邻接表存储法的示例代码：

class AdjacencyListGraph:
    def __init__(self):
        self.graph = {}

    def add_vertex(self, v):
        if v not in self.graph:
            self.graph[v] = []

    def add_edge(self, v1, v2):
        self.add_vertex(v1)
        self.add_vertex(v2)
        self.graph[v1].append(v2)
        self.graph[v2].append(v1)  # 对于无向图

    def remove_edge(self, v1, v2):
        self.graph[v1].remove(v2)
        self.graph[v2].remove(v1)  # 对于无向图

    def get_adjacency_list(self):
        return self.graph

# 示例使用
graph = AdjacencyListGraph()
graph.add_edge(0, 1)
print(graph.get_adjacency_list())  # 输出: {0: [1], 1: [0]}
graph.remove_edge(0, 1)
print(graph.get_adjacency_list())  # 输出: {0: [], 1: []}

在这个实现中，我们创建了一个`AdjacencyListGraph`类，它有一个字典`graph`来存储邻接表，以及四个方法：`__init__`来初始化图，`add_vertex`来添加顶点，`add_edge`来添加边，`remove_edge`来删除边，以及`get_adjacency_list`返回图的邻接表表示。

## 2.3 边集数组存储法

### 2.3.1 边集数组存储法的原理和特点

边集数组存储法是将图中所有的边存储在数组中的一种方法。每个边由一对顶点表示，因此每条边可以存储为一个包含两个顶点的元素。边集数组适合用于表示带权图，其中可以存储额外的信息，如边的权重。

边集数组存储法的特点包括：
- **空间效率**：对于稀疏图，边集数组能够节省空间，因为它只存储实际存在的边。
- **动态性**：添加和删除边较为简单，只需在数组中添加或移除元素即可。
- **边的遍历**：边的遍历通常比邻接矩阵更有效率，因为它不需要遍历整个矩阵。

### 2.3.2 边集数组存储法的算法实现

边集数组存储法可以使用结构体或类来表示每条边，并将它们存储在一个数组中。以下是使用Python实现边集数组存储法的示例代码：

class Edge:
    def __init__(self, src, dest, weight):
        self.src = src
        self.dest = dest
        self.weight = weight

class EdgeListGraph:
    def __init__(self):
        self.edge_list = []

    def add_edge(self, src, dest, weight):
        edge = Edge(src, dest, weight)
        self.edge_list.append(edge)

    def remove_edge(self, src, dest, weight):
        self.edge_list = [edge for edge in self.edge_list if not (edge.src == src and edge.dest == dest and edge.weight == weight)]

    def get_edge_list(self):
        return self.edge_list

# 示例使用
graph = EdgeListGraph()
graph.add_edge(0, 1, 10)
print(graph.get_edge_list())  # 输出: [Edge(src=0, dest=1, weight=10)]
graph.remove_edge(0, 1, 10)
print(graph.get_edge_list())  # 输出: []

在这个实现中，我们创建了一个`Edge`类来表示边，以及一个`EdgeListGraph`类来表示图，它有一个列表`edge_list`来存储边，并包含`add_edge`来添加边，`remove_edge`来删除边，以及`get_edge_list`返回图的边集数组表示。

# 3. 网络算法中的图存储创新应用

图形存储不仅是数据结构的组成部分，也是实现各种网络算法的关键基础。随着网络规模的扩大和应用需求的日益复杂化，如何在保持高效性能的同时，对图数据进行存储和处理变得尤为重要。本章将深入探讨图存储在一些核心网络算法中的创新应用，包括最短路径算法、网络流算法以及图的遍历与搜索算法等。

## 3.1 最短