【数据结构深度分析】：红黑树特性解析及在高效查找中的应用案例

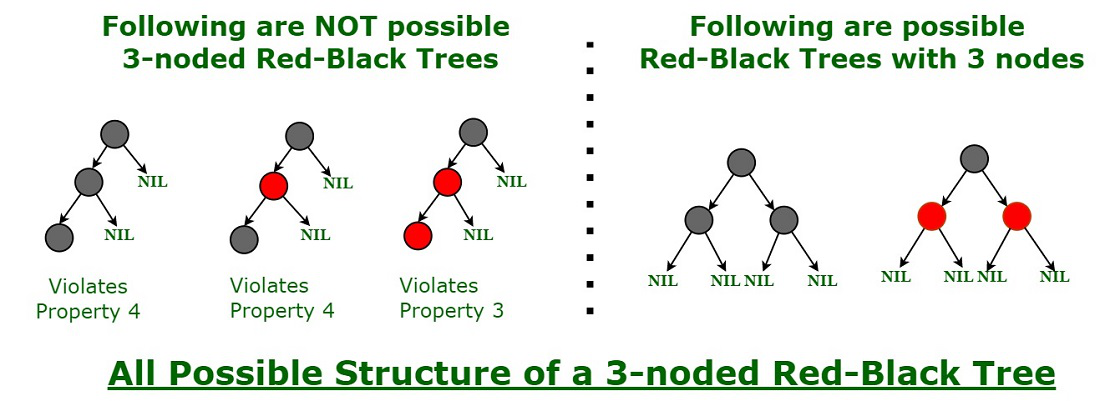
# 1. 红黑树的基本概念和特性

## 1.1 红黑树简介

红黑树是一种自平衡的二叉搜索树，它在每个节点上增加了一个存储位表示节点的颜色，可以是红色或黑色。通过对任何一条从根到叶子的路径上各个节点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出两倍，因而是近似平衡的。

## 1.2 重要性与应用

红黑树的重要性体现在其高效的搜索、插入和删除操作。其平衡性质使得这些操作的最坏情况下时间复杂度均为O(log n)，这使得红黑树非常适合于实现关联数组。红黑树广泛应用于诸如Java的TreeMap和TreeSet、C++ STL的map、multimap、multiset以及Linux内核中的调度器等。

## 1.3 基本特性

- 每个节点要么是红的，要么是黑的。
- 根节点是黑的。
- 每个叶子节点（NIL节点，空节点）是黑的。
- 如果一个节点是红的，那么它的两个子节点都是黑的。
- 对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑节点。

# 2. 红黑树的理论基础

## 2.1 红黑树的定义和性质

### 2.1.1 红黑树的五个基本性质

红黑树是一种自平衡的二叉查找树，它在每个节点上增加了一个存储位来表示节点的颜色，可以是红色或黑色。通过对任何一条从根到叶子的路径上各个节点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出两倍，因而是近似平衡的。

红黑树的五个基本性质如下：
1. 每个节点要么是红色，要么是黑色。
2. 根节点是黑色。
3. 所有叶子节点（NIL节点，空节点）都是黑色。
4. 每个红色节点的两个子节点都是黑色的（也就是说从每个叶子到根的所有路径上不能有两个连续的红色节点）。
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

### 2.1.2 红黑树与AVL树的比较

AVL树是一种高度平衡的二叉搜索树，任何节点的两个子树的高度最大差别为1，这使得AVL树在增加、删除、查找操作时能够保持较好的平衡性，但维护这种平衡需要频繁的旋转操作。

红黑树与AVL树相比有以下区别和优缺点：
- AVL树在查找性能上通常优于红黑树，因为AVL树的平衡性更高。
- 红黑树在插入和删除性能上优于AVL树，因为它在维护平衡时进行的操作比AVL树要少。
- 红黑树允许出现稍微不平衡的情况，因此它的旋转次数和维护成本更低，特别是在插入和删除操作中。

在需要频繁插入和删除的场合，红黑树往往能提供更好的性能。

## 2.2 红黑树的节点插入

### 2.2.1 插入操作的理论基础

红黑树的插入操作主要包含两个部分：首先是将新节点以二叉查找树的方式插入到树中，此时新节点的父节点被标记为红色，然后通过一系列的颜色调整和树的旋转来维持红黑树的五个性质。

插入节点的过程中可能会出现的冲突主要与性质4有关：新插入的红色节点不能有一个红色的父节点。这通常需要调整父节点、祖父节点以及可能的叔叔节点的颜色，并可能需要进行树的旋转。

### 2.2.2 插入后的颜色调整和平衡处理

在插入节点并标记为红色之后，可能会违反红黑树的性质，需要进行如下调整：
1. 如果新插入节点的父节点是黑色，那么插入操作不会影响红黑树的性质。
2. 如果新插入节点的父节点是红色，那么就需要检查父节点的兄弟节点（叔叔节点）的颜色，并根据叔叔节点的颜色采取不同的策略：
- 叔叔节点是红色：只需重新着色并检查祖父节点。
- 叔叔节点是黑色：需要进行一系列的旋转操作，并可能涉及到重新着色。

进行旋转操作时，可以是单旋转（左旋或右旋）或双旋转（先左旋再右旋，或者先右旋再左旋），旋转的目的是重新分布节点，以保持树的平衡。

## 2.3 红黑树的节点删除

### 2.3.1 删除操作的理论基础

红黑树的删除操作比插入更为复杂。删除节点通常涉及到用一个子节点来替换被删除的节点，这个替换节点（通常为被删除节点的中序后继）可能是红色也可能是黑色。如果替换节点是红色，删除操作比较简单；如果是黑色，则需要对树进行调整，以保持红黑树的性质。

在删除节点后，可能会违反性质5（红黑树的路径上黑色节点的数量必须相同），这需要通过颜色调整和树的旋转来解决。

### 2.3.2 删除后的颜色调整和平衡处理

删除节点后，如果替换节点是黑色，会减少某条路径上的黑色节点数量，违反性质5。调整策略通常如下：
1. 如果一个黑色节点被删除，尝试找到一个节点来临时替代它的角色，比如它的兄弟节点或其子节点。
2. 通过重新着色和旋转操作来“传播”黑色的缺失。
3. 如果必须删除的是根节点，而根节点是黑色，那么将根节点染成红色，这样性质5仍然保持有效（因为没有路径的黑色节点数减少了）。

调整的过程是复杂的，并且可能需要多次的旋转和颜色调整才能恢复树的平衡。在实现删除算法时，需要仔细考虑所有可能的情况。

graph TD
    A[开始删除节点] --> B[确定替换节点]
    B --> C{替换节点颜色}
    C -->|红色| D[简单删除]
    C -->|黑色| E[复杂调整]
    D --> F[结束]
    E --> G[寻找替代黑色节点]
    G --> H{替代节点}
    H -->|兄弟节点| I[重新着色和旋转]
    H -->|子节点| J[重新着色和旋转]
    I --> F
    J --> F

以上流程图展示了红黑树删除节点后的基本处理逻辑。

本章节详细介绍了红黑树的理论基础，包括其定义、性质、插入和删除操作的详细分析。在下一章，我们将继续探讨红黑树的算法实现，包括旋转操作、插入算法实现和删除算法实现等内容。

# 3. 红黑树的算法实现

## 3.1 红黑树的旋转操作

### 3.1.1 左旋和右旋的定义及性质

红黑树的核心操作之一是旋转操作，它分为左旋和右旋两种。旋转操作用于在插入和删除节点时保持红黑树的平衡性。左旋定义为以某个节点x为中心，将它的右子节点y提升为x的父节点，同时将x变为y的左子节点。右旋则相反，它以节点x为中心，将它的左子节点y提升为x的父节点，x则变为y的右子节点。

#### 左旋操作

左旋操作的几何性质保证了树的有序性不被破坏，并且旋转后所有节点的左子树仍然小于右子树。左旋操作的伪代码如下：

左旋(T, x)
    y ← 右子节点[x]
    x.右子节点 ← y.左子节点
    if y.左子节点 ≠ 空
        y.左子节点.父节点 ← x
    y.父节点 ← x.父节点
    if x.父节点 = 空
        T ← y
    else if x = x.父节点.左子节点
        x.父节点.左子节点 ← y
    else
        x.父节点.右子节点 ← y
    y.左子节点 ← x
    x.父节点 ← y

#### 右旋操作

右旋操作的伪代码如下：

右旋(T, x)
    y ← 左子节点[x]
    x.左子节点 ← y.右子节点
    if y.右子节点 ≠ 空
        y.右子节点.父节点 ← x
    y.父节点 ← x.父节点
    if x.父节点 = 空
        T ← y
    else if x = x.父节点.左子节点
        x.父节点.左子节点 ← y
    else
        x.父节点.右子节点 ← y
    y.右子节点 ← x
    x.父节点 ← y

### 3.1.2 旋转操作在维护红黑树性质中的作用

旋转操作在红黑树的维护中起着至关重要的作用。当树中插入或删除节点后，可能会导致红黑树的五个性质中的一个或多个被破坏。通过应用旋转操作，我们可以在O(1)的时间内恢复这些性质，保持树的平衡。在插入操作中，如果插入的节点是红色，且其父节点也是红色，这将导致两个连续的红色节点，违反了红黑树的性质4。此时，通过适当的旋转和重新着色操作，可以修正这一问题。在删除操作中，为了保持树的平衡，可能会需要多次旋转操作来调整树结构。

## 3.2 红黑树的插入算法实现

### 3.2.1 插入步骤详解

红黑树的插入操作主要分为以下几个步骤：

1. 将新节点着色为红色，并像在普通二叉搜索树中那样插入新节点。
2. 通过递归或循环的方式检查插入节点的父节点，如果父节点是黑色，不需要进一步操作；如果父节点是红色，那么需要进行颜色调整和可能的旋转操作。
3. 经过调整后，如果根节点的颜色发生了变化，需要将其重新着色为黑色。

### 3.2.2 插入后调整过程及代码实现

调整过程可能会涉及到多次的旋转操作。以下是一个简化的插入后调整的伪代码实现，它展示了如何在插入后维护红黑树的性质：

红黑树插入调整(T, 新节点)
    while 新节点.父节点 是 红色 do
        if 新节点.父节点 = 新节点.祖父节点.左子节点 then
            y ← 新节点.父节点.父节点.右子节点
            if y 是 红色 then
                新节点.父节点 ← 黑色
                y ← 黑色
                新节点.祖父节点 ← 红色
                新节点 ← 新节点.祖父节点
            else
                if 新节点 = 新节点.父节点.右子节点 then
                    新节点 ← 新节点.父节点
                    左旋(T, 新节点)
                end if
                新节点.父节点 ← 黑色