【数据结构进阶】：揭秘平衡二叉树(B-Trees)的高效存储与性能优化

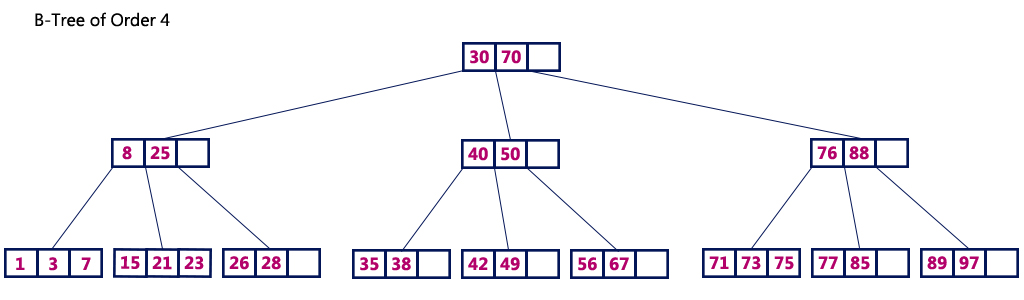
# 1. 平衡二叉树基础概念

在信息技术的广泛领域中，平衡二叉树（Balanced Binary Tree）是数据结构中的一个重要组成部分，对于存储和管理数据具有极高的效率。平衡二叉树允许快速检索、插入和删除操作，其核心优势在于保证了树的平衡，从而确保操作的性能不会随着数据量的增加而大幅下降。最为人熟知的平衡二叉树包括AVL树和红黑树，而本章将聚焦在这些树结构的基础概念，为后续章节中深入探讨更为复杂的B-Trees（B树）和其他相关数据结构打下坚实的基础。

# 2. 深入理解B-Trees的结构与特性

## 2.1 B-Trees的基本定义

### 2.1.1 B-Trees的数学基础

B-Trees（平衡多路查找树）是一种自平衡的树数据结构，它维护数据的排序，并允许在对数时间内进行搜索、顺序访问、插入和删除等操作。B-Trees是数据库和文件系统中常用的索引结构。数学上，我们可以将B-Trees看作是在二叉查找树的基础上扩展出来的，能够管理大量数据的树结构。

B-Trees特别适合读写大块数据的存储系统，比如磁盘存储器。其关键在于最小化磁盘I/O操作，因为它能够将多个元素存储在单个节点中。这样的结构不仅减少了树的高度，还提高了磁盘存取效率。我们可以将B-Trees视为高度平衡的多路树，其中每个节点可以拥有比二叉树更多的子节点。

### 2.1.2 B-Trees的关键属性

B-Trees的关键属性包括：

- 所有的叶子节点都在同一层。
- 每个节点最多有m个子节点，其中m是树的阶。
- 除了根节点和叶子节点之外，每个节点最少有ceil(m/2)个子节点。
- 一个节点含有k个子节点时，它必定包含k-1个关键字（key）。
- 所有的非叶子节点都可以看作是子树的索引。
- 每个节点中的关键字都是按顺序排列的。

这些属性确保了树的平衡性，并且使得树的高度保持在对数级别，这样即便是非常大的数据集也能够实现高效的查找。

## 2.2 B-Trees的节点结构和算法

### 2.2.1 节点分裂与合并

节点分裂和合并是B-Trees维护平衡的关键操作。节点分裂通常发生在节点插入关键字后超过了最大容量时。分裂操作将该节点分为两个节点，并将中位数关键字提升到父节点，以此来维持树的平衡性。

节点合并发生在删除关键字导致节点关键字数量小于最小允许值时。此时，需要从相邻的兄弟节点中借用一个关键字，并与其合并。如果相邻兄弟节点也没有足够的关键字，则它们会合并为一个节点，并且父节点的一个关键字会下降来保证树的平衡。

### 2.2.2 B-Trees的查找算法

B-Trees的查找算法类似于二叉查找树的查找方法，但是需要处理多路分支。查找操作从根节点开始，将给定值与节点中的关键字进行比较，根据比较结果，决定查找的下一个节点是当前节点的哪一个子节点。这个过程一直重复，直到找到对应的值，或者到达叶子节点且未找到值为止。

### 2.2.3 B-Trees的插入与删除操作

B-Trees的插入操作首先按照查找算法找到合适的位置，然后将新的关键字添加到节点中。如果节点的关键字数量超过了最大值，则执行节点分裂操作。

删除操作则稍微复杂，需要找到待删除的关键字。如果关键字在叶子节点上，直接删除即可；如果关键字在非叶子节点上，通常用该节点的中序后继（或前驱）关键字来替换，然后删除中序后继（或前驱）关键字。删除可能导致节点的关键字数量减少，必要时执行节点合并操作。

## 2.3 B-Trees的时间复杂度分析

### 2.3.1 最坏情况下的性能表现

在最坏的情况下，B-Trees的所有节点都是满的，此时插入和删除操作可能触发一系列的节点分裂或合并，使得从树根到叶子的路径上每个节点都可能被分裂或合并。对于一个阶数为m的B-Tree，其高度h可以表示为：h ≤ log_m(n+1)/2。因此，最坏情况下的时间复杂度是O(log n)。

### 2.3.2 最佳情况与平均情况分析

在最佳情况下，即所有节点都只使用了最小容量（不包括根节点），B-Trees的高度将保持最低。对于一个阶数为m的B-Tree，高度可以表示为：h = ceil(log_m(n+1)/2)。因此，最佳情况下的时间复杂度也是O(log n)。

平均情况下，B-Trees的性能表现介于最坏和最佳情况之间。由于B-Trees的平衡特性，平均操作时间通常接近最优时间复杂度，这使得B-Trees成为处理大量数据的高效数据结构之一。

# 3. B-Trees的实战应用

## 3.1 B-Trees在数据库系统中的应用

### 3.1.1 B-Trees在索引结构中的角色

在数据库系统中，B-Trees扮演着至关重要的角色，特别是在索引结构的设计和实现上。索引是一个帮助数据库管理系统快速定位数据行的技术。没有索引，数据库系统可能需要进行全表扫描来找到特定的数据行，这在数据量大的情况下是非常低效的。B-Trees作为平衡树的一种，能够保证查询、插入和删除操作在对数时间内完成，这使得它们成为了实现数据库索引结构的理想选择。

B-Trees能够将数据存储在有序的结构中，这对于范围查询尤为重要。例如，在一个按日期排序的日志文件中，使用B-Tree索引可以快速定位到特定日期范围内的日志条目。B-Trees的这一特性在数据库系统中被广泛用来优化查询性能，尤其是涉及范围查找和排序的查询。

### 3.1.2 数据库操作中的性能提升实例

在现代数据库系统中，B-Trees索引的应用实例比比皆是。以MySQL的InnoDB存储引擎为例，InnoDB使用B+Tree作为索引的数据结构。假设有一个电商网站，其数据库包含一个商品信息表，该表通过商品ID、名称、价格等多个字段来存储信息。为了提升搜索商品的性能，开发者会在商品ID上建立一个索引。

当用户想要搜索特定价格范围内的商品时，数据库可以通过B-Tree索引快速定位到价格字段在该范围内的记录，而不需要扫描整个商品表。这不仅减少了数据检索的时间，也降低了对系统资源的消耗。此外，由于B-Trees的平衡特性，即使在高并发的环境下，数据库操作的性能也不会有太大的波动，保证了查询的一致性。

## 3.2 B-Trees与其他数据结构的比较

### 3.2.1 B-Trees与红黑树的比较

B-Trees与红黑树都是为了解决二叉搜索树在插入和删除操作时可能退化成链表的问题，导致查找效率从O(log n)变为O(n)。然而，它们在实现和使用上有很大的不同。

红黑树是一种自平衡的二叉搜索树，它通过维持一系列的平衡规则来保证树的平衡，如节点颜色、叔叔节点颜色以及红黑性质的调整。而B-Trees是一种多路平衡搜索树，它允许每个节点有更多的子节点，通常用于磁盘存储系统中，可以减少磁盘I/O次数，提高效率。

在内存数据结构的比较中，红黑树在查找效率上与B-Trees相比较有优势，因为它只涉及最多O(log n)的内存访问。但是，在处理磁盘数据时，B-Trees由于其节点容量大，可以减少磁盘访问的次数，所以在大型数据库和文件系统中更受欢迎。

### 3.2.2 B-Trees与AVL树的比较

AVL树是另一种自平衡的二叉搜索树，它的每个节点的平衡因子（即左子树的高度与右子树的高度之差）只可能是-1、0或1。AVL树的这种高度平衡特性使得查找操作非常高效，但同时也带来了更频繁的树调整操作，即在每次插入或删除节点后都可能需要旋转操作来维持树的平衡。

相比之下，B-Trees由于其多路分支的特性，调整平衡的代价要比AVL树小得多。在插入或删除操作后，B-Trees的平衡调整通常是通过节点分裂或合并来完成，这比AVL树的旋转操作要简单。因此，B-Trees在插入和删除操作上通常有更好的性能，特别是在需要处理大量更新操作的应用场景中。

## 3.3 B-Trees的代码实现

### 3.3.1 B-Trees基本操作的代码示例

以下是使用伪代码实现的B-Tree插入操作的示例。请注意，这只是为了演示B-Tree操作的基本逻辑，实际的实现会根据具体的编程语言和应用环境有所不同。

function BTreeInsert(T, k):
    t := T.root
    if t is NULL:
        T.root := createNode()  // 创建一个新节点作为根
        T.root.keys := [k]
    else:
        t := BTreeInsertNonRoot(T, t, k)
    if t is full:
        u := splitNode(t)  // 分裂节点
        i