heapq与二叉堆：图解Python中的优先级队列操作

# 1. 优先级队列与二叉堆的基本概念

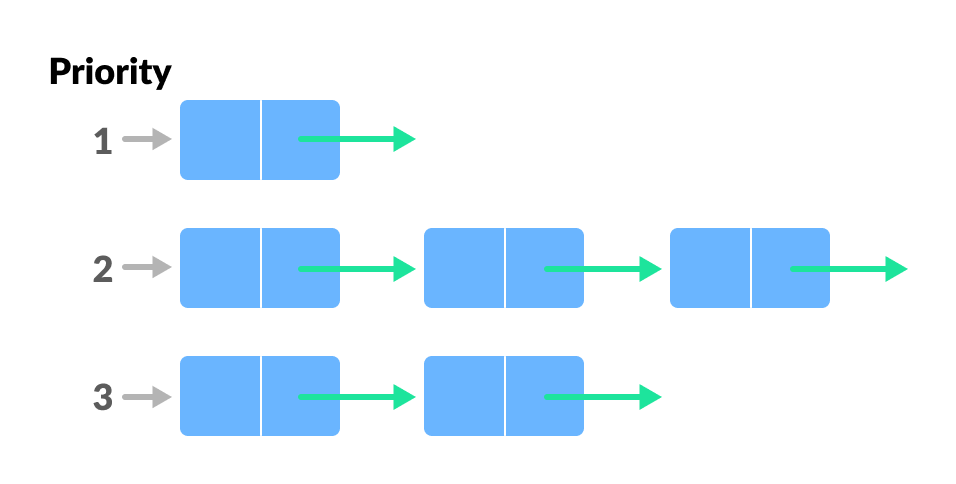
优先级队列是一种抽象数据类型，其中的元素都有自己的优先级。在优先级队列中，元素按照优先级从高到低的顺序被移除。它与先进先出（FIFO）的普通队列不同，因为普通队列移除元素的顺序只取决于它们进入队列的顺序。

二叉堆是优先级队列的一种实现方式，具体来说，它是一种特殊的完全二叉树。在二叉堆中，树的每一层都是完全填满的，除了可能的最后一层。二叉堆分为两种：最大堆和最小堆。在最大堆中，任何一个父节点的值都大于或等于其子节点的值；而在最小堆中，父节点的值则小于或等于其子节点的值。

通过理解优先级队列和二叉堆的基本概念，我们为进一步深入探讨二叉堆的理论基础和实际应用打下了基础。接下来，我们将探索二叉堆的理论基础，揭示其在数据结构中的独特地位。

# 2. 二叉堆的理论基础

## 2.1 优先级队列的原理

### 2.1.1 优先级队列的定义

优先级队列是一种抽象数据类型，允许插入数据的同时保持队列中元素的有序性。不同于普通队列遵循的先进先出（FIFO）原则，优先级队列中的元素根据优先级进行排列，优先级最高的元素总是在队列的最前面。

在优先级队列中，每个元素都有一个优先级属性，该属性定义了元素在队列中的排列顺序。当进行插入操作时，新元素将根据其优先级被放置在合适的位置，而不是简单地放在队列尾部。同样地，在移除操作中，总是移除当前优先级最高的元素。

### 2.1.2 优先级队列的使用场景

优先级队列广泛应用于各种场景，包括但不限于以下几种：

- **任务调度系统：** 在需要根据任务优先级进行调度的系统中，优先级队列可以保证高优先级的任务得到先处理。
- **事件驱动模拟：** 例如模拟一个消防系统，需要根据火警事件的紧急程度来决定出警的顺序。
- **网络协议：** 在某些网络协议中，数据包的传输需要根据优先级来决定顺序，如在网络拥塞时，优先发送高优先级的数据包。
- **图算法：** 在处理图的广度优先搜索（BFS）时，优先级队列（最小堆）用于确保节点按照距离源点的长度顺序被访问。

## 2.2 二叉堆的数学模型

### 2.2.1 完全二叉树的特点

二叉堆是基于完全二叉树的一种数据结构，具有以下特点：

- **层级性：** 除了最后一层外，每一层都被完全填满，而最后一层的节点则集中在左侧。
- **索引关系：** 对于树中的任意节点，其索引为`i`，其左孩子的索引为`2*i+1`，右孩子的索引为`2*i+2`，其父节点的索引为`(i-1)/2`。
- **完全填满：** 每一层都是完全填满的，除了可能的最后一层。

由于完全二叉树的这些特性，二叉堆能够在O(1)时间复杂度内访问父节点和子节点，这使得其在执行堆操作时更加高效。

### 2.2.2 二叉堆的性质和分类

二叉堆可以分为两种主要类型：最大堆和最小堆。

- **最大堆：** 在最大堆中，任何一个父节点的值总是大于或等于其子节点的值。最大堆通常用于实现优先级队列，当需要频繁地删除最大元素时。
- **最小堆：** 在最小堆中，任何一个父节点的值总是小于或等于其子节点的值。最小堆适合于需要频繁删除最小元素的应用场景。

二叉堆的这两个性质使得堆操作能够高效进行，特别是当堆被用来实现优先级队列时，可以快速地找到并删除最小元素。

## 2.3 二叉堆的操作算法

### 2.3.1 插入（heapify up）算法

插入操作是向二叉堆中添加新元素的过程，其目的是在添加新元素后保持堆的性质。插入新元素通常是在堆的末尾进行，然后通过`heapify up`过程将元素移动到其适当的位置。这个过程不断地比较新元素与其父节点的值，并在必要时交换它们的位置，直到满足最大堆或最小堆的性质为止。

以下是一个最小堆中插入元素的伪代码示例：

def heapify_up(heap, index):
    # 获取当前节点的值
    new_value = heap[index]
    # 不断向上与父节点比较
    while index > 0:
        # 获取父节点的索引
        parent_index = (index - 1) // 2
        # 父节点的值
        parent_value = heap[parent_index]
        # 如果当前节点值小于父节点值，则满足最小堆性质，停止
        if new_value >= parent_value:
            break
        # 否则，交换父节点和当前节点的值
        heap[index] = parent_value
        heap[parent_index] = new_value
        # 更新索引，继续向上进行heapify
        index = parent_index

# 插入元素，先添加到数组末尾
heap.append(new_value)
# 然后进行heapify up
heapify_up(heap, len(heap) - 1)

### 2.3.2 删除最小元素（heapify down）算法

删除最小元素是从二叉堆中移除根节点（在最小堆中是值最小的元素），然后用堆的最后一个元素替代根节点，接着进行`heapify down`过程，将新的根节点向下移动到正确的位置，以保持堆的性质。

`heapify down`的过程与`heapify up`相反，从根节点开始，将其与其较小的子节点进行比较，并在必要时交换位置，直到无法继续交换为止。

def heapify_down(heap, index):
    # 获取要下沉的节点值
    value_to_move = heap[index]
    # 获取节点的子节点索引
    left_child_index = 2 * index + 1
    right_child_index = 2 * index + 2
    # 循环直到没有子节点或子节点都不小于值
    while left_child_index < len(heap):
        # 选择较小的子节点索引
        child_index = left_child_index
        # 检查是否有右子节点，并比较大小
        if right_child_index < len(heap) and heap[right_child_index] < heap[left_child_index]:
            child_index = right_child_index
        # 如果子节点小于要移动的值，继续下沉过程
        if heap[child_index] < value_to_move:
            heap[index] = heap[child_index]
            index = child_index
            left_child_index = 2 * index + 1
            right_child_index = 2 * index + 2
        else:
            # 如果所有子节点都比要移动的值大，则到达正确位置
            break
    # 最后将原始值放到当前位置
    heap[index] = value_to_move

# 删除最小元素
min_value = heap[0]
heap[0] = heap[-1]
heap.pop()
heapify_down(heap, 0)

以上代码展示了如何在最小堆中进行插入和删除最小元素的操作，通过这些堆化过程，堆结构能够保持其特定的性质，从而在优先级队列等应用中发挥关键作用。

# 3. heapq模块的实践应用

## 3.1 heapq模块简介

### 3.1.1 heapq模块的安装和导入

`heapq`模块是Python标准库的一部分，因此无需单独安装