【heapq在复杂数据处理中的应用】：策略与优化技巧

# 1. heapq模块概述与基础应用

在Python编程中，heapq模块是处理优先队列和堆栈结构的一个重要工具。该模块提供了堆队列算法的实现，也就是通常所说的优先队列算法。本章将对heapq模块进行概述，并介绍其在基础应用中的使用方法。我们首先了解heapq模块的基本功能和使用场景，然后演示如何使用该模块构建和操作堆，从而为后续章节中复杂数据结构的处理和性能优化打下基础。

## 1.1 heapq模块功能概述

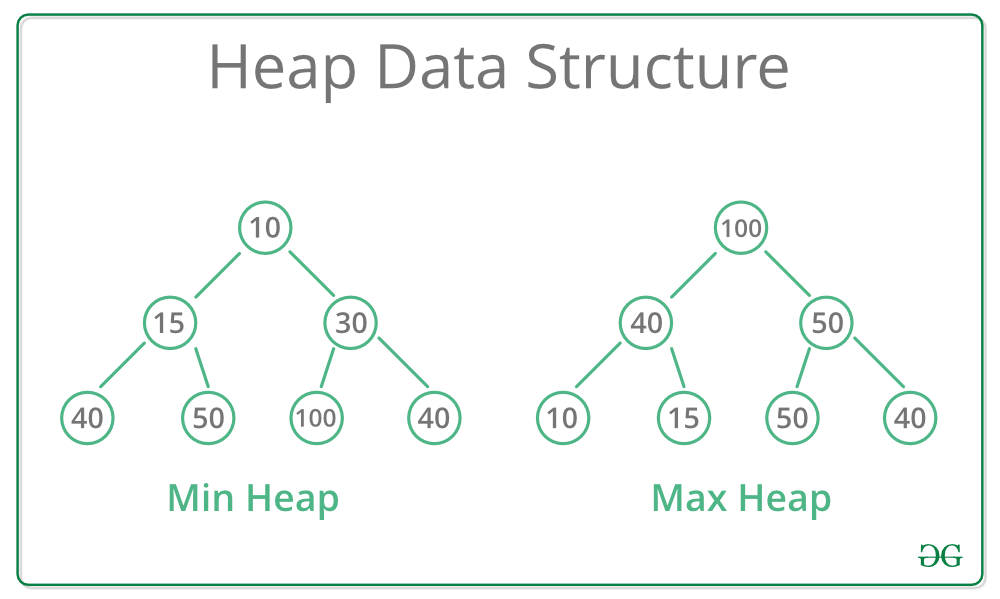
heapq模块实现了堆队列算法，提供了以下两种堆结构：
- 最小堆（min-heap）：堆中的任意父节点的值总是不大于其子节点。
- 最大堆（max-heap）：堆中的任意父节点的值总是不小于其子节点。

通过heapq提供的方法，可以轻松完成堆的创建、插入元素、弹出元素等基本操作，从而实现优先队列的功能。

## 1.2 heapq模块在基础应用中的使用

在基础应用中，heapq模块最常见的用途是实现优先队列。例如，在任务调度、事件驱动编程或图搜索算法中，需要根据元素的优先级来决定处理顺序，此时可使用heapq构建优先队列。

以下是使用heapq模块创建最小堆的示例代码：

import heapq

# 初始化一个空堆
heap = []

# 向堆中添加元素
heapq.heappush(heap, (0, 'task1'))  # 添加一个元组，第一个元素为优先级
heapq.heappush(heap, (1, 'task2'))

# 弹出堆顶元素，根据优先级排序
while heap:
    priority, task = heapq.heappop(heap)
    print(f"处理任务: {task}, 优先级: {priority}")

通过上述代码，我们创建了一个最小堆，并使用heappop方法按照优先级依次处理了队列中的任务。heapq模块的使用使得优先队列的操作变得简单明了。在接下来的章节中，我们将深入探讨heapq模块的高级应用和优化技巧。

# 2. 复杂数据结构的优先队列实现

在深入了解堆（heap）这一数据结构后，我们转向如何利用Python标准库中的`heapq`模块实现优先队列。本章节将讨论优先队列的结构，实现复杂元素排序的技巧，以及使用堆处理多维数据的挑战和解决方案。

## 2.1 优先队列的数据模型

### 2.1.1 优先队列的概念和应用场景

优先队列是一种特殊的队列，在队列中，元素的出队顺序是由元素的优先级决定的。在很多需要对任务或数据进行排序的场景中，优先队列是一个非常有用的抽象。

例如，在操作系统中，进程调度器需要根据进程的优先级来决定哪个进程获得处理机；在网络数据包处理中，紧急的或需要优先传输的数据包会放在队列的前面；在任务调度系统中，紧急的任务会优先被安排执行。

### 2.1.2 heapq模块构建优先队列的方法

在Python中，`heapq`模块提供了一个非常方便的方法来实现优先队列。堆本质上是一种特殊的完全二叉树，也称为二叉堆（binary heap），其中每个节点都不大于（或不小于）其子节点，这被称为堆属性。

`heapq`模块提供了如下两个重要的功能来构建优先队列：

- `heapq.heappush(heap, item)`: 将item项添加到heap堆中，保持堆的不变性。
- `heapq.heappop(heap)`: 弹出并返回堆中最小（默认行为）或最大元素，保持堆的不变性。

import heapq

# 创建一个空堆
heap = []

# 将多个元素加入堆中
heapq.heappush(heap, (1, '任务1'))
heapq.heappush(heap, (5, '任务2'))
heapq.heappush(heap, (2, '任务3'))

# 弹出最小元素
print(heapq.heappop(heap))  # 输出: (1, '任务1')

## 2.2 复杂元素的优先队列操作

### 2.2.1 定制排序键的实现技巧

优先队列的元素往往不是单一的数据类型，而是包含多个属性的复杂对象。为了实现定制排序，我们可以使用Python的元组或类的比较机制。

考虑一个任务列表，每个任务都有优先级和名称，我们希望优先级越高的任务越先出队：

import heapq

# 定义一个任务类，包含优先级和名称
class Task:
    def __init__(self, priority, name):
        self.priority = priority
        self.name = name
    # 定义比较方法，使得堆根据优先级进行排序
    def __lt__(self, other):
        return self.priority < other.priority

# 创建任务列表
tasks = [Task(3, '任务1'), Task(1, '任务2'), Task(2, '任务3')]

# 将任务加入到堆中
heap = [task for task in tasks]
heapq.heapify(heap)

# 弹出最小元素
print(heapq.heappop(heap).name)  # 输出: '任务2'

### 2.2.2 元素更新与重新排序

在优先队列的操作中，有时候我们需要更新队列中的元素优先级。这种情况下，我们不能简单地修改元素，因为这样做会破坏堆的结构。`heapq`模块不直接支持就地更新，但我们可以通过移除并重新添加元素的方式来实现：

# 假设任务1的优先级需要提升到0
heapq.heappush(heap, heapq.heappop(heapq.heappush(heap, (0, '任务1'))))

## 2.3 heapq与多维数据处理

### 2.3.1 多维数据排序的挑战

处理多维数据时，我们面临的主要挑战是如何在多个属性之间找到一个合适的排序逻辑。例如，在一个包含多个属性（如x和y坐标）的点集合中，我们可能希望按照某个特定的顺序（如先按x坐标排序，若相同再按y坐标排序）对这些点进行排序。

### 2.3.2 堆数据结构在多维数据中的应用

使用堆来处理多维数据时，我们可以在将元素添加到堆中之前预先计算一个排序键（sort key）。这个排序键可以是一个元组，其中每个元素对应一个维度的值，并根据我们的排序要求进行排序。

import heapq

# 定义一个点类
class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    # 定义比较方法
    def __lt__(self, other):
        return (self.x, self.y) < (other.x, other.y)

# 创建点的列表
points = [Point(1, 2), Point(3, 1), Point(2, 1)]

# 使用heapq创建一个最小堆
heap = [(p.x, p.y, p) for p in points]
heapq.heapify(heap)

# 弹出最小元素
print(heapq.heappop(heap)[2].x, heapq.heappop(heap)[2].y)  # 输出: 2 1 3 1

以上展示了如何在Python中利用`heapq`模块实现优先队列，以及如何处理复杂和多维数据结构。接下来的章节将深入探讨`heapq`在算法优化和数据处理中的应用。

# 3. heapq在算法优化中的应用

heapq模块不仅能够帮助我们快速实现优先队列等数据结构，还可以在算法优化方面发挥巨大作用。在这一章节中，我们将深入探讨heapq如何被应用来改进算法性能，特别是在堆化操作、排序算法和图论中的实际案例。

## 3.1 heapify操作与算法效率

### 3.1.1 heapify过程的内部原理

heapq模块的核心操作之一是heapify过程，它允许将一个普通的列表转换成一个堆结构。这个过程涉及到的关键步骤是调整列表中的元素，以确保满足堆的性质，即父节点的值总是小于或等于其子节点的值（在最小堆的情况下）。

要了解heapify的内部原理，首先需要明白堆结构的特点。堆是一种特殊的完全二叉树，它通常用数组来实现。在堆中，对于任意节点i（数组索引从0开始），其子节点的位置分别是2*i+1和2*i+2，而其父节点的位置是(i-1)//2。heapify的核心是一个名为`siftDown`的操作，它从数组的最后一个非叶子节点开始，向上调整整个树结构。

siftDown操作确保每个父节点都满足堆性质。这个过程是自底向上进行的，当一个父节点与其子节点中的最大（或最小）者交换后，它可能还需要与新子节点进一步调整。这种交换和调整会在整个树结构中进行，直到满足堆性质。

### 3.1.2 heapify对算法性能的影响

heapify操作的时间复杂度为O(n)，空间复杂度为O(1)，这使得它在处理大量数据时非常高效。在算法优化中，通过使用heapify来初始化一个堆，可以避免使用更复杂的排序算法，如快速排序或归并排序。

在需要频繁进行插入或删除操作的场合，heapify尤其有用。因为插入和删除操作都需要重新调整堆的结构，而通过heapify进行局部调整通常比重建整个堆要快。例如，在处理优先队列或模拟事件时，这种效率的提升是非常显著的。

## 3.2 heapq在排序算法中的角色

### 3.2.1 heapq与快速排序、归并排序的比较

在排序算法领域，快速排序和归并排序是两种常用且效率较高的算法。然而，这两种算法都存在一定的缺点：快速排序在最坏情况下的时间复杂度为O(n^2)，而归并排序则需要额外的O(n)空间来存储数据副本。

heapq可以用来实现一种基于堆的排序算法——堆排序。堆排序的时间复杂度为O(nlogn)，与快速排序相同，但是堆排序能够在原地进行排序，不需要额外的空间（除了输入数组本身）。这意味着heapq能够提供一个性能稳定且空间效率高的排序算法。

### 3.2.2 heapq在稳定排序中的应用

稳定排序意味着排序操作不会改变具有相同键值的元素之间的原始顺序。在某些应用场景中，维持元素的相对顺序非常重要。例如，在处理包含时间戳的日志数据时，如果后发生的事件在排序中先于先前的事件出现，可能会导致逻辑上的错误。

传统的堆排序算法并不保证稳定性，但是在Python中，由于heapq模块提供了对元组的支持，我们可以巧妙地利用元组的稳定性来实现稳定的堆排序。具体方法是使用元组作为堆元素，其中第一个元素为排序键，第二个元素为原始数据索引。在比较元素时，仅比较元组中的第一个元素，从而实现稳定排序。

## 3.3 heapq在图论中的应用案例

### 3.3.1 Dijkstra算法中的 heapq 应用

Dijkstra算法是图论中用于寻找单源最短路径的算法。在算法实现中，需要频繁地从一组待访问的顶点中选出距离最小的顶点，这恰好是优先队列的典型应用场景。