【heapq库文件探究】：从入门到精通的进阶之路

# 1. heapq库概述

Python中的`heapq`模块提供了一种实现堆队列算法（优先队列）的方式。该模块实现的是一种称为二叉堆的堆结构，它能够高效地支持优先级队列操作。由于其简单易用和性能优良的特点，`heapq`在数据处理、任务调度以及算法设计等领域有着广泛的应用。

在本文的第一章中，我们将介绍`heapq`模块的基本概念、设计目的及其在Python生态系统中的定位。通过本章，读者将对`heapq`模块有一个初步的认识，并理解其在解决实际问题中的潜在价值。

## 1.1 heapq模块的起源与发展

`heapq`模块在Python标准库中已经存在多年，它的出现部分是为了解决数据处理中的排序和优先级问题。它提供了简洁的API，使得构建和操作堆变得简单直接，无需手动实现复杂的堆调整算法。随着Python语言的不断升级和优化，`heapq`模块也得到了相应的改进，以提供更好的性能和用户体验。

## 1.2 heapq模块的特性与优势

`heapq`模块最显著的特点是其简洁性和效率。它使用二叉堆的结构，可以快速地在堆顶插入元素和移除堆顶元素，而这两个操作的时间复杂度分别为O(log n)。此外，堆的维护操作也非常高效，它保证了堆的“堆序性”，即任何一个父节点的值都小于或等于其子节点的值。

让我们用一个简单的例子来说明heapq的应用：

import heapq

# 创建一个空堆
heap = []

# 插入数据
heapq.heappush(heap, (5, 'write code'))
heapq.heappush(heap, (1, 'read book'))
heapq.heappush(heap, (3, 'practice problems'))

# 获取堆顶元素
print(heapq.heappop(heap))  # 输出: (1, 'read book')

此代码段展示了如何使用`heapq`模块创建一个最小堆，并通过`heappush`函数添加元素，`heappop`函数则用于获取堆顶元素，它返回堆中最小的元素。通过这一简单的示例，我们便可以体会到heapq模块的便捷性和实用性。

接下来，我们将深入探讨heapq库的基本操作原理，带领读者理解其背后的数据结构和算法原理。

# 2. heapq基本操作原理

## 2.1 heap的数据结构特性

### 2.1.1 堆的概念与分类
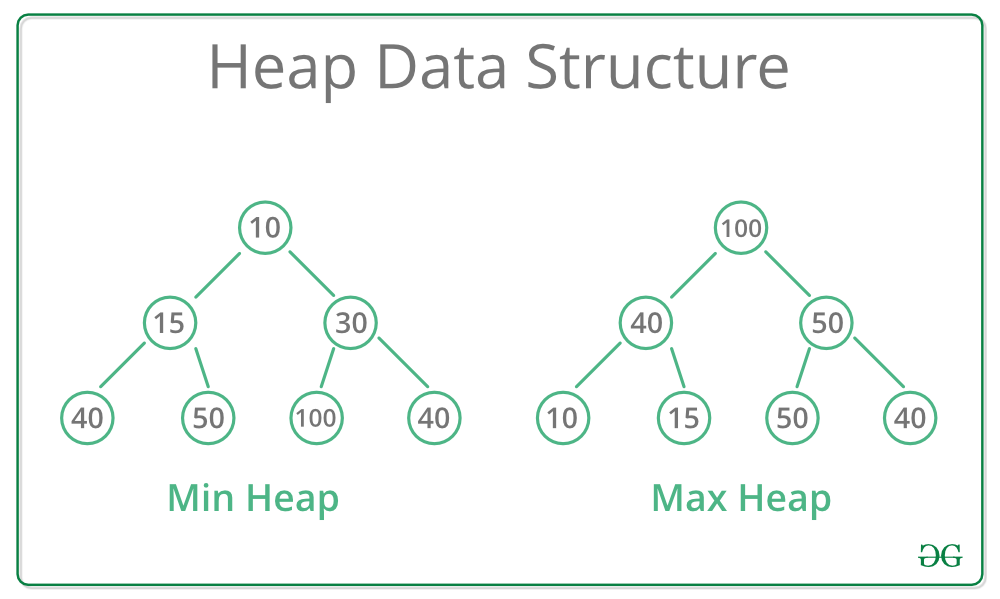
堆（Heap）是一种特殊的完全二叉树，它满足堆性质：任何一个父节点的值都必须大于或等于（在最大堆中）或小于或等于（在最小堆中）其子节点的值。根据这个性质，堆可以被分类为最大堆和最小堆。最大堆中父节点的值总是大于或等于子节点的值，而最小堆则相反。堆这种数据结构非常适合于实现优先队列和其他需要进行高效插入和删除最大（或最小）元素的场景。

在Python中，heapq模块仅实现了最小堆的优先队列功能，使得任何父节点的值都小于或等于其子节点的值。这样的设计使得最小元素总是在堆的顶端，方便进行高效的检索和删除操作。

### 2.1.2 堆的性质和堆序性
堆的性质决定了其作为数据结构的核心特性——堆序性（Heap Property）。最小堆的堆序性表明了对于树中任意节点，该节点的值都不大于其子节点的值。这种性质对于实现快速检索最小元素是非常有用的，因为它确保了最小元素总是在堆的根节点。在最大堆中，堆序性则是相反的，每个父节点的值都不小于其子节点的值。

堆序性的维护，是通过一系列称为"堆调整"（Heapify）的操作来完成的。当堆结构受到插入或删除等操作的破坏时，堆调整可以快速恢复堆序性，保证堆的正确性。这种动态调整堆的性质，是实现高效堆操作的关键所在。

## 2.2 heapq库的主要函数介绍

### 2.2.1 堆的创建和初始化
在Python中，可以通过heapq模块来创建和初始化堆。最简单的创建方式是使用`heapq.heapify()`函数，它能够把一个普通的列表转换成一个最小堆。例如：

import heapq

# 初始化列表
lst = [3, 1, 6, 5, 2, 4]

# 将列表转换为堆
heapq.heapify(lst)

print(lst)  # 输出: [1, 2, 4, 5, 3, 6]

在这个例子中，`heapq.heapify()`函数接受一个列表，并且在原地修改这个列表，将其调整为最小堆的形态。需要注意的是，`heapq.heapify()`函数的时间复杂度为O(n)，其中n是列表中元素的数量。

### 2.2.2 元素的插入和删除
对于堆来说，最核心的操作莫过于元素的插入和删除。`heapq`模块提供了`heappush()`和`heappop()`两个函数来分别执行这两种操作。

- `heappush(heap, item)`: 将item元素添加到heap堆中。这个操作会保持堆的特性。
- `heappop(heap)`: 弹出并返回堆中最小的元素。由于这个操作会改变堆的大小，它会通过调整来维持最小堆的特性。

这里有一个例子：

import heapq

# 创建空堆
heap = []

# 推入元素
for n in [1, 5, 3, 4, 2]:
    heapq.heappush(heap, n)

print(heap)  # 输出: [1, 2, 3, 4, 5]

# 弹出最小元素
print(heapq.heappop(heap))  # 输出: 1

print(heap)  # 输出: [2, 4, 3, 5]

通过这个简单的例子，我们可以看到如何将一个列表转换成堆，以及如何插入和删除元素，而维持其作为最小堆的特性。

## 2.3 heapq的算法原理分析

### 2.3.1 堆调整过程解析
堆调整（Heapify）是堆操作中的核心算法。它负责维护堆序性，当堆中的某个子树不再满足最小堆的性质时，会重新调整这个子树，以保证整个堆满足堆序性。

在插入和删除操作中，最简单的调整策略是：

- 插入操作：把新元素放到堆的末尾，然后通过一系列的上浮（或称为上升）操作，直到满足堆序性为止。
- 删除操作：删除堆顶元素，然后把堆的最后一个元素放到根部，通过一系列的下沉（或称为下降）操作，直到满足堆序性为止。

下沉操作尤其重要，因为它需要在违反堆序性的条件下，将一个节点与其子节点中较小（或较大）的一个交换，直到它成为叶子节点或满足堆序性为止。

### 2.3.2 时间复杂度探讨
在分析`heapq`模块中堆操作的时间复杂度时，我们通常会关注两个基本操作：插入和删除。

- 插入（heappush）操作的时间复杂度为O(log n)，其中n是堆中元素的数量。这是因为插入新元素后可能需要执行上浮操作，堆的层数为log n，最多需要移动log n个节点来恢复堆序性。
- 删除（heappop）操作的时间复杂度也为O(log n)。删除堆顶元素后，把最后一个元素放到根部，接着执行下沉操作，直到满足堆序性为止。同样地，这个过程中最多需要移动log n个节点。

因此，如果我们将插入和删除操作看作是单个操作，那么堆可以被看作是支持log n时间复杂度的操作的数据结构。