【数据处理巧匠】：如何利用R语言的density函数轻松处理异常值

# 1. 数据处理与R语言概述

数据处理是数据分析和统计推断的基础，而R语言凭借其强大的数据处理能力，在科研和商业领域受到了广泛的青睐。本章将概述R语言的基本知识及其在数据处理中的应用。

## 1.1 R语言简介

R语言是一种专门用于统计分析、图形表示和报告的编程语言。它拥有一个庞大且活跃的社区，提供了丰富的包来扩展其基础功能。R语言的优势在于它强大的数据处理能力、灵活的图形系统和高效的数据结构。

## 1.2 R语言在数据处理中的作用

在数据处理过程中，R语言能够执行各种操作，如数据导入导出、清洗、转换、探索性数据分析和统计建模等。利用R语言的向量化操作，可以高效处理大量数据集，而其内置的绘图函数，如plot、hist等，可以帮助用户直观地理解数据特征。

## 1.3 R语言的学习路径

对于初学者而言，学习R语言的最佳途径是通过实践项目和案例研究。从基本的数据操作开始，逐步深入理解高级的数据结构和统计模型。此外，社区论坛和文档是学习R语言不可或缺的资源。

# 例如，安装和加载常用的R包
install.packages("tidyverse") # 安装tidyverse包集合
library(tidyverse) # 加载包集合

本章为读者搭建了一个理解R语言和数据处理的框架。接下来的章节将深入探讨R语言中用于处理数据的特定函数和高级技巧。

# 2. density函数的基础知识

### 2.1 R语言数据结构介绍

在R语言中，数据结构是处理和存储数据的基础。掌握基本的数据结构对于使用density函数进行数据分析至关重要。我们将探讨向量、矩阵与数据框以及因子与列表。

#### 2.1.1 向量、矩阵与数据框

向量是R中最基本的数据结构，可以存储数值、字符或逻辑值。矩阵是二维的数值型数据结构，数据按行或列排列。数据框（data frame）则是类似于矩阵，但可以存储不同类型数据的二维数据结构。数据框是数据分析中最常用的数据结构之一，因为它能够容纳各种类型的数据，非常适合于实际数据集。

# 创建一个向量
vector_example <- c(1, 2, 3, 4, 5)

# 创建一个矩阵
matrix_example <- matrix(1:12, nrow = 3, ncol = 4)

# 创建一个数据框
data_frame_example <- data.frame(
  ID = 1:4,
  Name = c("Alice", "Bob", "Charlie", "David"),
  Age = c(21, 22, 23, 24)
)

在上述代码中，我们创建了一个基本的向量、矩阵和数据框示例。向量是单列的，而矩阵是一个3行4列的数值矩阵。数据框包含有标识符、名称和年龄三列，这类似于数据库中的表格结构。

#### 2.1.2 R语言中的因子与列表

因子（factor）在R语言中用于表示分类数据，它能够存储字符值，并且这些值是预定义的类别。列表（list）是R中最灵活的数据结构，它可以包含不同类型和维度的数据。

# 创建一个因子
factor_example <- factor(c("High", "Medium", "Low", "High"))

# 创建一个列表
list_example <- list(
  name = "John",
  age = 30,
  scores = c(88, 92, 79),
  is_student = TRUE
)

在这段代码中，我们创建了一个因子，它表示的是数据集中的某种分类变量。而列表可以包含多个不同类型的数据，例如姓名、年龄、成绩和学生状态。

### 2.2 density函数的语法解析

density函数是R语言中用于估计连续变量概率密度函数的工具。它是数据分析和统计建模中的一个关键函数。

#### 2.2.1 density函数的参数与返回值

density函数的基本语法是：

density(x, ...)

这里的`x`是一个数值型向量，表示要进行密度估计的数据。`...`可以包含其他参数，如`bw`（带宽参数，控制平滑程度），`kernel`（核函数类型，默认为高斯核）等。

函数返回一个包含密度估计结果的对象，包括x坐标（密度图中的x轴值）和密度值（y轴值）。

# 使用density函数
density_result <- density(data_frame_example$Age)

# 查看返回值的结构
str(density_result)

上述代码计算了`data_frame_example`中`Age`列数据的密度估计，并用`str`函数查看返回值的结构。

#### 2.2.2 如何阅读density函数的输出图

density函数的输出可以使用`plot()`函数绘制出密度图，其中x轴代表数据值，y轴表示每个数据值出现的概率密度。

# 绘制密度图
plot(density_result)

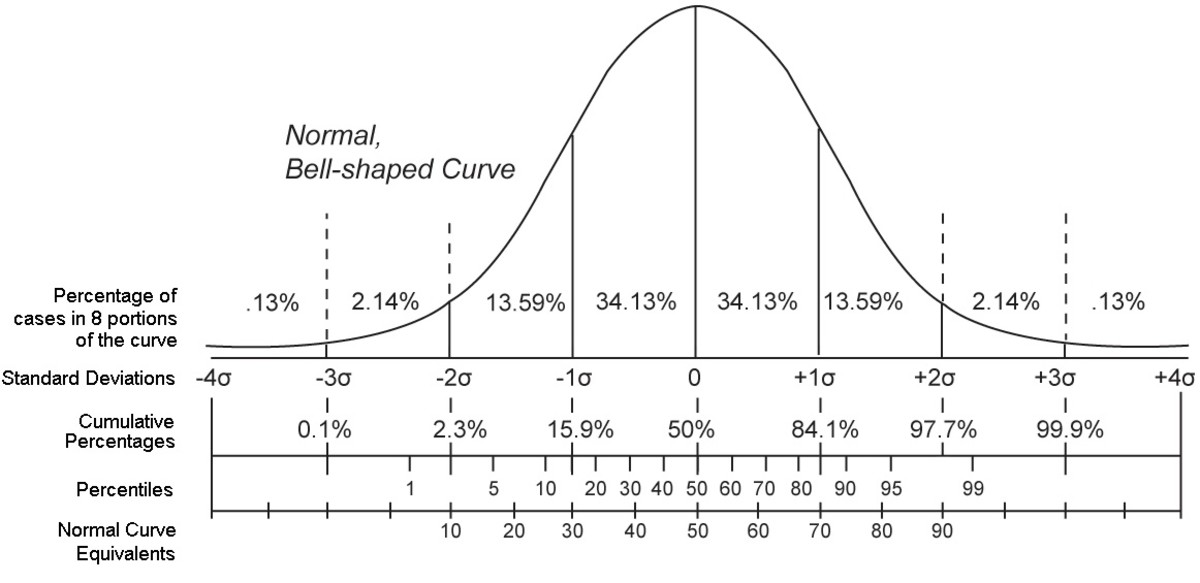
绘制出的密度图能够直观显示数据的分布情况，通过图形可以识别出数据的中心趋势、分布的对称性和峰度。异常值的存在通常表现为密度图上的小峰或低谷。

### 2.3 异常值定义与识别方法

异常值是与数据集中的其他数据显著不同的数据点。在统计学中，异常值的检测对于数据分析的准确性和可靠性至关重要。

#### 2.3.1 统计学中的异常值标准

统计学中有多种方法定义和识别异常值。一种常用的方法是使用标准差或者四分位距（IQR）准则。

# 计算均值和标准差
mean_value <- mean(data_frame_example$Age)
sd_value <- sd(data_frame_example$Age)

# 计算上下界
upper_bound <- mean_value + 3 * sd_value
lower_bound <- mean_value - 3 * sd_value

# 使用四分位距（IQR）识别异常值
IQR_value <- IQR(data_frame_example$Age)
upper_bound_IQR <- quantile(data_frame_example$Age, 0.75) + 1.5 * IQR_value
lower_bound_IQR <- quantile(data_frame_example$Age, 0.25) - 1.5 * IQR_value

在这段代码中，我们使用均值加减三倍标准差的方法定义上下界，并用四分位距方法确定了上下界值。超过这些界限的值可以被认为是异常值。

#### 2.3.2 可视化工具在异常值检测中的应用

可