【R语言统计基石】：深入理解密度估计与density函数的统计学意义

# 1. R语言与统计学基础

在数据科学的世界中，统计学是理解数据和进行数据分析的基石。本章将带你领略R语言在统计学中的应用，以及如何利用R语言进行基本的统计分析。我们将从统计学的基本概念出发，逐步深入了解R语言在数据处理、统计推断、模型拟合等方面的功能。通过本章的学习，你将能够掌握R语言进行统计分析的基础，并为进一步探索复杂统计方法打下坚实的基础。

## 1.1 R语言简介

R语言是一种专门用于统计分析和图形表示的编程语言，它提供了丰富的统计函数和图形工具。R语言因其开源和强大的社区支持而被广泛使用。本节将介绍R语言的安装、基础语法以及如何在R环境中进行数据操作和基本分析。

# 安装R语言
install.packages("stats")  # 安装基本统计包

# 导入数据
data("mtcars")             # 加载内置数据集
summary(mtcars)            # 数据概览

# 基本统计分析
mean(mtcars$mpg)           # 计算平均值
var(mtcars$mpg)            # 计算方差

## 1.2 统计学基础概念

统计学涉及数据的收集、分析、解释和呈现。在本节中，我们将讨论描述统计和推断统计的基本概念，包括均值、中位数、标准差、置信区间和假设检验。这些概念是理解更高级统计方法和机器学习算法的前提。

- **描述统计**：提供数据集的概要性描述，例如平均值、中位数、众数和标准差等。
- **推断统计**：允许我们基于样本数据对总体进行估计和假设检验。
- **置信区间**：在一定的置信水平下，我们预期总体参数（如均值）落在一个区间内。
- **假设检验**：用于检验关于总体参数的特定假设是否成立。

通过上述概念的学习，你将能够更好地理解后续章节中密度估计的应用，并将统计学原理应用于R语言的实践中。

# 2. 密度估计理论详解

### 2.1 密度估计的概念与重要性
#### 2.1.1 从直方图到密度估计
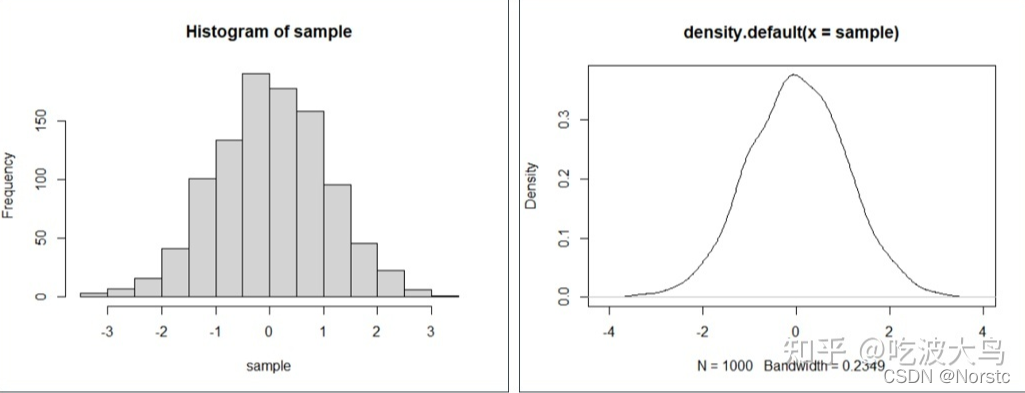
直方图是统计学中一种基本的数据可视化工具，它通过将数据分布划分为一系列连续的区间（也称为“箱子”或“bin”）并对每个区间的频数进行计数，用矩形的高低表示这些频数。虽然直方图能够大致地描绘出数据的分布形状，但它依赖于区间的选择，且相邻矩形间存在间隔，无法提供平滑的数据估计。

密度估计通过构建连续的概率密度函数（PDF）来解决直方图的局限性，能够给出数据分布的平滑估计。其核心思想是在每个数据点周围添加一个“小山丘”形状的函数，通常是高斯（正态）分布，然后将所有的“小山丘”叠加起来形成一个连续的曲线。这条曲线就是估计得到的概率密度函数，它能够更准确地描绘数据的分布情况，并提供平滑的估计。

# R语言中创建直方图的示例代码
hist(rnorm(100), main="Histogram of Normal Distribution", xlab="Value", ylab="Frequency")

在上述代码中，`rnorm(100)` 生成了100个标准正态分布的随机样本，`hist` 函数用来绘制这些数据的直方图。通过观察直方图，我们可以对数据分布的中心趋势和离散程度有一个大致了解。

#### 2.1.2 密度估计在统计推断中的作用
在统计推断中，密度估计为理解数据的潜在分布提供了基础。通过密度估计，统计学家和数据科学家可以对数据的总体分布做出假设，进而进行参数估计、假设检验和预测等统计推断任务。

例如，在参数估计中，我们可能基于样本数据估计总体的均值和方差。密度估计可以提供样本数据的概率模型，从而使得这种估计变得更为准确。假设检验中，我们可能需要确定数据是否符合某种特定的分布（例如正态分布），密度估计可以帮助我们更直观地验证这一点。

在实际应用中，密度估计尤其在金融风险分析、生物信息学和机器学习等领域发挥着重要作用。比如，在金融市场中，通过对股票价格或投资组合收益的数据进行密度估计，可以更好地进行风险管理，制定投资策略。

### 2.2 密度估计方法
#### 2.2.1 核密度估计(KDE)的基本原理
核密度估计（Kernel Density Estimation，KDE）是一种非参数密度估计方法，它通过核函数对每个样本点周围的密度进行平滑估计，进而综合所有点的贡献得到整个数据集的密度曲线。核函数是KDE中的核心概念，常见的核函数包括高斯核、均匀核、三角核等。每个核函数都围绕一个样本点定义了一个局部的密度分布，核的宽度（带宽）控制着核函数的影响范围。

# R语言中使用核密度估计的一个简单例子
x <- rnorm(100) # 生成100个标准正态分布的随机样本
density_obj <- density(x) # 使用density函数进行核密度估计
plot(density_obj, main="Kernel Density Estimate")

在这段代码中，`density` 函数是R语言基础包提供的，可以直接进行核密度估计。其核心参数包括样本数据向量 `x` 和带宽（未指定时采用默认值）。该函数返回一个包含估计密度值和对应点的密度对象，可以通过 `plot` 函数进行可视化。

#### 2.2.2 参数估计与非参数估计的比较
参数估计和非参数估计是统计学中两种基本的估计方法。参数估计依赖于对总体分布的先验知识，例如假设数据服从正态分布，然后利用样本数据来估计这些分布的参数（如均值和方差）。而非参数估计不假设数据遵循任何特定的分布，如核密度估计就是一种常见的非参数估计方法。

在实际应用中，参数估计方法较为简单且计算效率较高，但对数据的分布假设较为严格。而核密度估计等非参数方法虽然计算复杂度较高，但不需要严格的分布假设，适用性更广。

#### 2.2.3 核函数的选择与窗宽调整
核函数的选择和带宽（窗宽）的确定是核密度估计中的重要问题。不同的核函数影响着密度估计的平滑程度和边缘效应。例如，高斯核函数是所有核函数中应用最广泛的一种，因其具有良好的数学性质。而三角核函数可能在边缘部分产生更多波动。

带宽的选择直接关系到估计的平滑程度。较大的带宽会导致估计过于平滑，可能会掩盖数据的真实特征；较小的带宽则可能导致过度拟合，即捕捉到数据中的噪声而非真实结构。

带宽的选取通常依赖于一些优化准则，如交叉验证方法（Cross-Validation）。通过调整带宽参数，可以平衡估计的偏差和方差，以获得更精确的密度估计。

### 2.3 密度估计的数学模型
#### 2.3.1 概率密度函数的数学定义
概率密度函数（Probability Density Function，PDF）是统计学中用于描述连续随机变量概率分布的函数。对于连续随机变量X，其概率密度函数f(x)满足两个条件：

1. f(x)在定义域内非负，即对于所有的x，有f(x) ≥ 0。
2. f(x)关于其定义域的积分等于1，即∫ f(x) dx = 1。

PDF的值本身并不是概率，而是概率的密度。当我们想要计算随机变量X落在某个特定区间[a, b]内的概率时，我们需要计算这个区间的PDF值的积分，即P(a ≤ X ≤ b) = ∫[a,b] f(x) dx。

#### 2.3.2 密度估计的无偏性与一致性
无偏性指的是估计量的期望值等于要估计的参数真值。密度估计的无偏性意味着估计得到的密度曲线平均而言与真实的概率密度函数是一致的。然而，在实际应用中，由于样本量的限制，往往很难获得完全无偏的密度估计。

一致性是指随着样本量的增加，估计量将收敛于要估计的参数真值。对于密度估计而言，一致性意味着当样本量趋于无限时，估计得到的概率密度函数将越来越接近真实的概率密度函数。

#### 2.3.3 交叉验证与带宽选择的方法论
交叉验证是一种统计模型选择方法，它通过保留一部分数据不参与模型训练，来评估模型对未知数据的泛化能力。在密度估计中，交叉验证常被用来选择最优的带宽参数。

交叉验证方法主要分为两类：留一交叉验证（Leave-One-Out Cross-Validation，LOOCV）和K折交叉验证。在密度估计中，我们通常使用留一交叉验证来选择带宽。其基本思想是，对于每一个可能的带宽参数值，我们重复以下过程：

1. 移除一个样本点。
2. 使用剩余的数据点进行密度估计。
3. 计算被移除的样本点处的概率密度估计值，并将其作为验证集的估计损失。

重复上述过程，我们可以得到每个带宽参数对应的平均估计损失，选择使得平均损失最小的带宽参数作为最终的带宽。

# 使用R语言中KDE进行LOOCV交叉验证的示例代码
library(ks) # 加载ks包，该包提供了核密度估计和交叉验证相关函数
x <- rnorm(100) # 生成数据
bw <- h