MATLAB低通滤波器性能优化指南：深入分析，提升信号处理效率

# 1. MATLAB低通滤波器简介

低通滤波器是一种允许低频信号通过而衰减高频信号的滤波器。在MATLAB中，可以使用`filter`函数来设计和应用低通滤波器。

MATLAB低通滤波器具有以下特点：

- **截止频率：**滤波器开始衰减信号的频率。
- **衰减率：**滤波器衰减信号的速率，以dB/十倍频程表示。
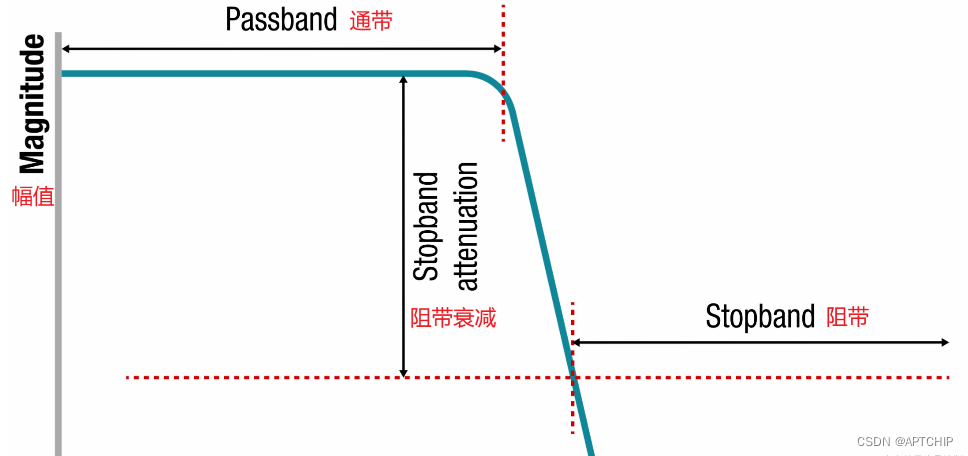
- **通带：**截止频率以下的频率范围，信号在此范围内基本不受衰减。
- **阻带：**截止频率以上的频率范围，信号在此范围内被衰减。

# 2. 低通滤波器性能分析

### 2.1 频率响应和相位响应

频率响应是指滤波器在不同频率下的幅度响应，而相位响应是指滤波器在不同频率下的相位偏移。

**频率响应**

对于低通滤波器，其频率响应通常表现为：

- 在低频段，幅度响应接近 1，表示滤波器允许低频信号通过。
- 在截止频率附近，幅度响应开始衰减，表示滤波器开始阻隔高频信号。
- 在高频段，幅度响应衰减到很小，表示滤波器有效阻隔了高频信号。

**相位响应**

低通滤波器的相位响应通常表现为：

- 在低频段，相位响应接近 0，表示低频信号通过滤波器时不会发生相位偏移。
- 在截止频率附近，相位响应开始变化，表示高频信号通过滤波器时会发生相位偏移。
- 在高频段，相位响应变化较大，表示高频信号通过滤波器时会发生明显的相位偏移。

### 2.2 截止频率和衰减率

**截止频率**

截止频率是指滤波器开始衰减信号的频率。通常，截止频率定义为滤波器幅度响应衰减到 3 dB（即 0.707 倍）时的频率。

**衰减率**

衰减率是指滤波器在截止频率后的幅度衰减速度。通常，衰减率用 dB/倍频程表示，表示滤波器在每个倍频程（频率翻倍）后的幅度衰减量。

### 2.3 通带和阻带

**通带**

通带是指滤波器允许通过的频率范围，通常从 0 Hz 到截止频率。在通带内，滤波器的幅度响应接近 1，相位响应接近 0。

**阻带**

阻带是指滤波器阻隔的频率范围，通常从截止频率到无穷大。在阻带内，滤波器的幅度响应衰减到很小，相位响应变化较大。

**示例：巴特沃斯低通滤波器**

巴特沃斯低通滤波器是一种常见的低通滤波器，其频率响应和相位响应如下：

**频率响应：**

H(f) = 1 / sqrt(1 + (f / fc)^2n)

其中：

* H(f) 为滤波器的幅度响应
* f 为输入信号的频率
* fc 为截止频率
* n 为滤波器阶数

**相位响应：**

φ(f) = -arctan(f / fc)

其中：

* φ(f) 为滤波器的相位响应
* f 为输入信号的频率
* fc 为截止频率

**代码块：巴特沃斯低通滤波器设计**

% 滤波器阶数
n = 5;

% 截止频率
fc = 100;

% 采样频率
fs = 1000;

% 创建巴特沃斯低通滤波器
[b, a] = butter(n, fc / (fs / 2));

% 频率响应和相位响应
[H, W] = freqz(b, a, 1024);

% 绘制频率响应和相位响应
figure;
subplot(2, 1, 1);
plot(W, 20 * log10(abs(H)));
title('频率响应');
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');

subplot(2, 1, 2);
plot(W, angle(H));
title('相位响应');
xlabel('频率 (Hz)');
ylabel('相位 (rad)');

**代码逻辑分析：**

* 使用 `butter` 函数创建巴特沃斯低通滤波器，并指定滤波器阶数 `n` 和截止频率 `fc`。
* 使用 `freqz` 函数计算滤波器的频率响应和相位响应。
* 绘制频率响应和相位响应，分别显示幅度和相位随频率的变化情况。

# 3.1 滤波器类型选择

在设计 MATLAB 低通滤波器时，首先需要选择合适的滤波器类型。MATLAB 中提供了多种滤波器类型，每种类型都有其独特的特性和应用场景。

| 滤波器类型 | 特性 | 应用场景 |
|---|---|---|
| 巴特沃斯滤波器 | 平坦的通带响应，单调衰减的阻带响应 | 一般用途滤波 |
| 切比雪夫 I 型滤波器 | 通带内无纹波，阻带内具有等纹波 | 要求高通带精度 |
| 切比雪夫 II 型滤波器 | 阻带内无纹波，通带内具有等纹波 | 要求高阻带衰减 |
| 椭圆滤波器 | 通带和阻带内都具有等纹波 | 要求高通带精度和阻带衰减 |

选择滤波器类型时，需要考虑以下因素：

* **通带和阻带要求：**确定所需的通带和阻带频率范围，以及允许的通带纹波和阻带衰减。
* **阶数：**滤波器阶数决定了滤波器的陡度和衰减率。
* **计算复杂度：**不同类型的滤波器具有不同的计算复杂度，需要考虑滤波器的实时性要求。

### 3.2 滤波器阶数和截止频率确定

确定滤波器类型后，需要确定滤波器的阶数和截止频率。

**滤波器阶数：**滤波器阶数决定了滤波器的陡度和衰减率。阶数越高，滤波器陡度越大，衰减率越高。但是，阶数越高，计算复杂度也越大。

**截止频率：**截止频率是滤波器通带和阻带的分界频率。通带内的频率分量将被滤波器通过，而阻带内的频率分量将被滤波器衰减。

确定滤波器阶数和截止频率的方法如下：

1. **根据通带和阻带要求：**根据通带和阻带的频率范围和允许的纹波和衰减，确定所需的滤波器阶数和截止频率。
2. **使用滤波器设计工具：**MATLAB 提供了滤波器设计工具，可以帮助用户根据指定的通带和阻带要求自动确定滤波器阶数和截止频率。

### 3.3 滤波器系数计算

确定滤波器类型、阶数和截止频率后，需要计算滤波器的系数。MATLAB 提供了 `butter`、`cheby1`、`cheby2` 和 `ellip` 等函数来计算不同类型滤波器的系数。

**滤波器系数计算步骤：**

1. **确定滤波器类型：**根据滤波器类型选择相应的函数，如 `butter`、`cheby1`、`cheby2` 或 `ellip`。
2. **指定滤波器阶数和截止频率：**将确定的滤波器阶数和截止频率作为函数的参数。
3. **计算滤波器系数：**函数将根据指定的滤波器类型、阶数和截止频率计算滤波器的系数。

% 设计一个 4 阶巴特沃斯低通滤波器，截止频率为 100 Hz
[b, a] = butter(4, 100, 'low');

**滤波器系数分析：**

滤波器系数包含两个向量：`b` 向量和 `a` 向量。

* `b` 向量包含滤波器的分子系数，用于计算滤波器的输出。
* `a` 向量包含滤波器的分母系数，用于计算滤波器的状态。

滤波器系数的长度等于滤波器的阶数加 1。

# 4. MATLAB低通滤波器优化

### 4.1 滤波器阶数优化

滤波器阶数是影响滤波器性能的重要参数。阶数越高，滤波器在截止频率附近的衰减率越大，但同时也会增加滤波器的延迟。因此，在选择滤波器阶数时，需要权衡衰减率和延迟之间的关系。

MATLAB中提供了多种方法来优化滤波器阶数。一种常用的方法是使用`fdesign.lowpass`函数。该函数可以根据指定的截止频率和衰减要求自动计算滤波器的阶数。

% 指定截止频率和衰减要求
cutoff_freq = 100; % Hz
attenuation = 60; % dB

% 使用fdesign.lowpass函数计算滤波器阶数
design = fdesign.lowpass('N,F3dB', cutoff_freq, attenuation);

% 获取滤波器阶数
order = design.order;

% 打印滤波器阶数
disp(['滤波器阶数：' num2str(order)]);

### 4.2 滤波器类型优化

MATLAB提供了多种类型的低通滤波器，包括巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器。每种类型的滤波器都有其独特的特性。

* **巴特沃斯滤波器：**具有平坦的通带和单调的阻带，但衰减率较低。
* **切比雪夫滤波器：**在阻带内具有波纹，但衰减率比巴特沃斯滤波器高。
* **椭圆滤波器：**在通带和阻带内都具有波纹，但衰减率最高。

选择滤波器类型时，需要考虑滤波器的具体应用场景和性能要求。

### 4.3 滤波器系数优化

滤波器系数是影响滤波器性能的另一个重要参数。MATLAB提供了多种方法来优化滤波器系数，包括：

* **使用滤波器设计工具箱：**MATLAB提供了`filterDesigner`工具箱，可以帮助用户设计和优化滤波器。
* **使用优化算法：**可以使用优化算法，如遗传算法或粒子群优化算法，来优化滤波器系数。

优化滤波器系数可以提高滤波器的性能，例如提高衰减率或减少延迟。

# 5. MATLAB低通滤波器应用

### 5.1 信号去噪

低通滤波器可用于去除信号中的高频噪声。噪声通常表现为信号中的快速变化或尖峰。通过应用低通滤波器，我们可以平滑信号并去除这些噪声分量。

% 原始信号
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] + randn(1, 10);

% 低通滤波器设计
b = fir1(10, 0.5); % 阶数为 10，截止频率为 0.5

% 滤波
y = filter(b, 1, x);

% 绘制结果
figure;
plot(x, 'r');
hold on;
plot(y, 'b');
legend('原始信号', '滤波信号');

### 5.2 信号平滑

低通滤波器还可以用于平滑信号。平滑可以去除信号中的快速变化，使信号更加平稳。

% 原始信号
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] + randn(1, 10);

% 低通滤波器设计
b = fir1(10, 0.2); % 阶数为 10，截止频率为 0.2

% 滤波
y = filter(b, 1, x);

% 绘制结果
figure;
plot(x, 'r');
hold on;
plot(y, 'b');
legend('原始信号', '平滑信号');

### 5.3 边缘检测

低通滤波器可用于边缘检测。边缘是图像中亮度或颜色快速变化的地方。通过应用低通滤波器，我们可以平滑图像并去除噪声。然后，我们可以使用边缘检测算法（例如 Sobel 算子）来检测图像中的边缘。

% 读取图像
I = imread('image.jpg');

% 灰度化
I = rgb2gray(I);

% 低通滤波器设计
b = fir1(10, 0.5); % 阶数为 10，截止频率为 0.5

% 滤波
I_filtered = filter2(b, I);

% 边缘检测
edges = edge(I_filtered, 'sobel');

% 显示结果
figure;
imshow(edges);
title('边缘检测结果');