【Java贪心算法:性能优化的秘诀】
发布时间: 2024-08-29 17:41:57 阅读量: 72 订阅数: 34 


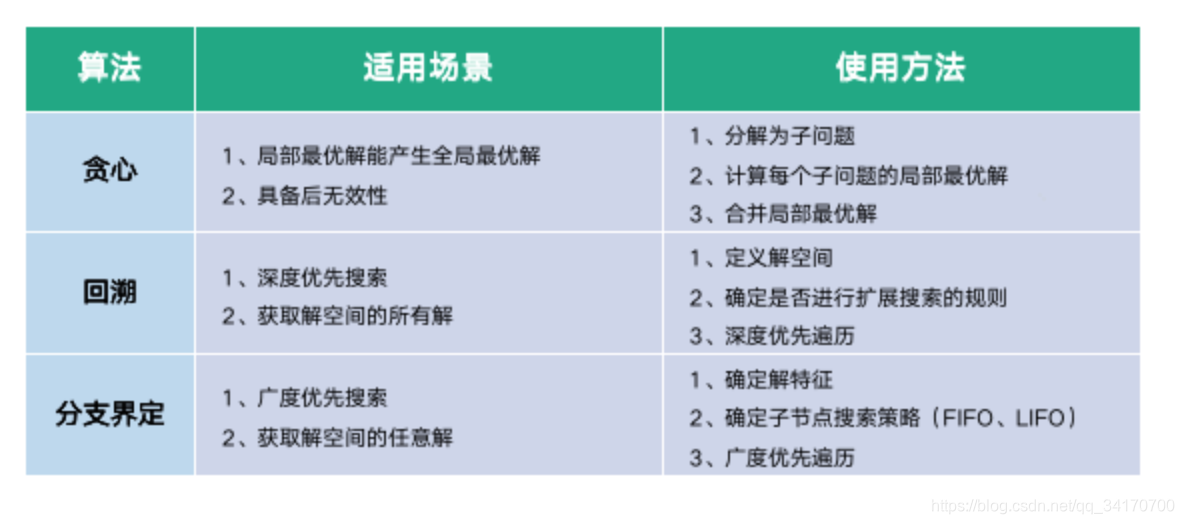
贪心算法:原理、应用及案例分析
# 1. 贪心算法的理论基础
贪心算法是一种在每一步选择中都采取当前状态下最优策略的算法,旨在求得全局最优解。它以局部最优解导向全局最优解,适用于具有最优子结构性质的问题。贪心算法的核心在于贪心选择原理,即通过局部最优选择来保证最终得到的是全局最优解。本章将从理论角度解析贪心算法的基本原理及其适用条件,为深入理解贪心算法打下坚实的基础。
## 1.1 贪心算法的基本概念
贪心算法在解决问题时,并不从整体最优解考虑,而是着眼于当前步骤的选择,通过局部最优解不断逼近全局最优解。在贪心算法中,可以认为每次选择都是在当前情况下能获得的最大收益,而忽略后续步骤的影响。这种方法依赖于问题具有贪心选择性质,即局部最优解能够导致全局最优解。
## 1.2 贪心算法的适用条件
并非所有问题都适合使用贪心算法来解决,它适用于具有以下两个重要性质的问题:
- **贪心选择性质**:通过局部最优选择能够确定全局最优解。
- **最优子结构**:一个问题的最优解包含其子问题的最优解。
不具备这两个性质的问题,使用贪心算法可能得到错误的答案。因此,在选择算法时,首先要分析问题是否符合贪心算法的适用条件。
## 1.3 贪心算法的局限性
虽然贪心算法在某些问题上非常高效,但也有其局限性。贪心算法不能保证解决所有优化问题,特别是那些不存在贪心选择性质的问题。此外,即使问题满足贪心选择性质,贪心算法也不一定能找到最优解,有时可能需要结合其他算法或者改进策略来找到真正的全局最优解。
了解贪心算法的理论基础对于掌握其核心概念和适用范围至关重要,这将为在实践中有效应用贪心算法奠定基石。接下来的章节将深入探讨在Java编程语言中如何实现和优化贪心算法,以及贪心算法在实际案例中的具体应用。
# 2. Java中实现贪心算法的核心机制
## 2.1 贪心策略的选择与定义
### 2.1.1 问题的实例化和贪心性质分析
贪心算法,作为一种解决问题的策略,总是做出在当前看来最优的选择,从而希望导致结果是全局最优的算法。在算法设计中,贪心算法是一类在每一步选择中都采取在当前状态下最好或最优的选择,从而希望导致结果是全局最好或最优的算法。贪心算法并不保证会得到最优解,但是在某些问题中贪心算法的解是最优的。
以经典的问题——找零钱问题为例:假设有面值为1, 5, 10, 25的硬币,如何用最少的硬币组合出某个金额?这个问题实际上就是贪心性质的。在每一步我们都选择当前可用硬币中面值最大的那个,因为这样我们能够用最少的硬币数量组合出需要的金额。
在Java中实现贪心算法,首先需要定义问题,并对问题的贪心性质进行分析。这是设计贪心算法的前提。例如,在解决硬币找零问题时,我们需要分析硬币的面值,确保当前面值的硬币选取得当,能够使总硬币数量最小。
### 2.1.2 贪心选择原理及其实现策略
贪心选择原理是贪心算法中最核心的原理之一。它是指在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优解考虑,它所做出的选择只是在某种意义上的局部最优选择。贪心选择后,问题规模会缩小,然后递归地做贪心选择,以达到全局最优解。
在Java中实现贪心算法时,通常需要定义一个类,其中包含求解贪心问题的主函数以及辅助函数。比如,我们创建一个名为`GreedySolver`的类来实现贪心算法,其中包含`solve()`方法来执行贪心选择和`subSolve()`方法来处理剩余问题。
下面是一个简化版的Java代码示例,演示了如何实现贪心选择原理:
```java
class GreedySolver {
// 用于存储贪心选择结果
private List<Integer> result = new ArrayList<>();
public List<Integer> solve(int[] denominations, int amount) {
// 将硬币面值按从大到小排序
Arrays.sort(denominations);
int remaining = amount;
for (int i = denominations.length - 1; i >= 0; i--) {
while (remaining >= denominations[i]) {
// 贪心选择当前面值最大的硬币
result.add(denominations[i]);
remaining -= denominations[i];
}
}
// 如果找零完成,返回结果
if (remaining == 0) {
return result;
} else {
// 如果不能精确找零,返回空列表
return Collections.emptyList();
}
}
}
public class Main {
public static void main(String[] args) {
int[] denominations = {25, 10, 5, 1};
GreedySolver solver = new GreedySolver();
List<Integer> change = solver.solve(denominations, 63);
System.out.println(change); // 输出结果为[25, 25, 10, 1, 1, 1]
}
}
```
通过上述代码我们实现了硬币找零问题的贪心算法。首先,将硬币面值进行降序排序,然后从最大面值的硬币开始,尽可能多地选择当前面值的硬币,直到不能选择更多的该面值硬币为止。随后,转向下一个较小面值的硬币,重复此过程,直到凑齐所需金额。
## 2.2 数据结构在贪心算法中的应用
### 2.2.1 优先队列与堆的应用
在贪心算法中,优先队列(Priority Queue)和堆(Heap)是经常使用的数据结构。它们可以快速地找到当前可选元素中的最优解,并进行相应的操作。优先队列允许我们按照优先级(一般用数值大小来定义)来存储元素,并且可以快速地取出优先级最高的元素。
在Java中,`PriorityQueue`类实现了优先队列的抽象数据类型,通常基于堆来实现。使用优先队列可以非常方便地实现贪心算法中的贪心选择策略。
下面是一个使用Java中的`PriorityQueue`来解决任务调度问题(类似活动选择问题)的示例:
```java
import java.util.PriorityQueue;
***parator;
class Activity implements Comparable<Activity> {
int start;
int finish;
// ... 其他属性和方法
@Override
public int compareTo(Activity other) {
***pare(finish, other.finish); // 按结束时间排序
}
}
class ActivitySelection {
public List<Activity> selectActivities(List<Activity> activities) {
// 按活动的结束时间排序
Collections.sort(activities);
PriorityQueue<Activity> pq = new PriorityQueue<>();
// 将第一个活动加入优先队列
pq.add(activities.get(0));
// 结果集合
List<Activity> selectedActivities = new ArrayList<>();
// 遍历所有活动
for (int i = 1; i < activities.size(); i++) {
// 如果优先队列的活动可以在当前活动之前完成
if (pq.peek().finish <= activities.get(i).start) {
pq.poll(); // 移除队列中的活动
}
pq.add(activities.get(i)); // 将当前活动加入优先队列
}
// 从优先队列中获取最终选择的活动
while (!pq.isEmpty()) {
selectedActivities.add(pq.poll());
}
return selectedActivities;
}
}
public class Main {
public static void main(String[] args) {
List<Activity> activities = new ArrayList<>();
// 假设添加了若干个活动
ActivitySelection solver = new ActivitySelection();
List<Activity> selected = solver.selectActivities(activities);
// 输出结果
}
}
```
在这个例子中,我们定义了一个`Activity`类,它实现了`Comparable`接口以允许按结束时间排序。然后,我们在`ActivitySelection`类中使用`PriorityQueue`来存储当前未被冲突的活动。每次从优先队列中选择最早结束的活动,并检查后续的活动是否和这个活动有时间上的冲突。如果一个活动可以在当前活动结束后立即开始,那么我们就可以选择它,否则我们保留当前活动。通过这种方式,我们可以找到能够参加的最大活动集合。
### 2.2.2 有序数据结构的选择与应用
除了优先队列,有序数据结构例如链表、二叉搜索树等也经常被用于贪心算法中。在Java中,我们可以使用`TreeMap`来维护有序的数据,或者使用`Collections.sort()`对数据进行排序。
有序数据结构的选择依赖于具体问题的需求。例如,在活动选择问题中,如果活动已经按结束时间排序,我们可以直接使用链表来维护活动序列,并在遍历过程中进行贪心选择。如果活动未排序,则可以使用`Collections.sort()`进行排序,或者使用`TreeMap`来维护有序的活动集合。
这里以活动选择问题为例,演示如何使用`TreeMap`来优化数据访问:
```java
import java.util.TreeMap;
class ActivitySelection {
public List<Activity> selectActivities(List<Activity> activities) {
// 使用TreeMap来维护结束时间到活动的映射
TreeMap<Integer, Activity> map = new TreeMap<>();
for (Activity activity : activities) {
map.put(activity.finish, activity);
}
List<Activity> selectedActivities = new ArrayList<>();
Activity lastSelected = null;
// 从最早结束的活动开始遍历
for (Map.Entry<Integer, Activity> entry : map.entrySet()) {
if (lastSelected == null || entry.getValue().start >= lastSelected.finish) {
selectedActivities.add(entry.getValue());
lastSelected = entry.getValue();
}
}
return selectedActivities;
}
}
```
在这个例子中,我们通过活动的结束时间将活动放入`TreeMap`中,然后遍历这个映射,选择结束时间最早且与上一个选择的活动没有冲突的活动。使用`TreeMap`的好处是,它能够快速地通过活动的结束时间找到对应的活动,提高了查找效率。
## 2.3 贪心算法的时间复杂度分析
### 2.3.1 常见贪心问题的时间复杂度计算
时间复杂度是评估算法效率的重要指标,它通常表示为算法执行时间与输入数据大小之间的关系。对于贪心算法,时间复杂度计算取决于问题的具体情况以及贪心策略的实现方式。对于某些贪心算法,由于每一步都直接做出最优选择,所以实现起来非常高效,具有较低的时间复杂度。然而,由于贪心算法并不保证总是能得到最优解,因此在某些问题上,设计高效的贪心算法可能会比较困难。
例如,对于经典的活动选择问题,贪心策略是按照活动的结束时间进行排序,然后选择第一个活动,并从剩余的活动中选择结束时间最早的活动,重复此过程直到无法再选择更多活动为止。此策略的时间复杂度主要由排序步骤决定。如果使用快速排序或归并排序对活动进行排序,那么时间复杂度为O(n log n),其中n是活动的数量。遍历排序后的活动列表并选择活动的时间复杂度为O(n),因此整个贪心算法的时间复杂度为O(n log n)。
### 2.3.2 时间复杂度优化技巧
尽管贪心算法在某些问题上已经很高效,但在处理大数据集时,任何能够减少算法时间复杂度的优化都是有价值的。优化贪心算法的一个常见技巧是减少排序操作的需要。例如,在硬币找零问题中,如果硬币面额有限并且经常重复使用,可以预先计算出各种面额的最优组合,并将其存储在哈希表中。当需要找零时,可以直接查询预计算的结果,从而将时间复杂度降低到O(1)。
另一种优化技巧是利用数据结构的特性,减少不必要的计算。例如,在活动选择问题中,我们可以使用`TreeMap`来管理活动,使得每个活动都能在O(log n)时间内被快速访问和插入,从而实现O(n log n)的时间复杂度。
一个简单的贪心算法优化案例是查找最近点对问题:给定一个平面上的n个点,找出其中最近的一对点的距离。贪心算法的一个解决方案是按照x坐标对所有点进行排序,然后遍历排序后的点集,使用一个优先队列(最小堆)来维护当前遇到的点中距离上一个点最近的点集。这样可以在O(n log n)时间复杂度内找到最近点对的距离。
下面是使用贪心策略在查找最近点对问题的Java代码示例:
```java
import java.util.Arrays;
import java.util.PriorityQueue;
class Point {
double x, y;
public Point(double x, double y) {
this.x = x;
this.y = y;
}
}
class PointDistanceComparator implements Comparator<Point> {
Point referencePoint;
public PointDistanceComparator(Point referencePoint) {
this.referencePoint = referencePoint;
}
@Override
public int compare(Point a, Point b) {
double distA = distance(this.referencePoint, a);
double distB = distance(this.referencePoint, b);
***pare(distA, distB);
}
private double distance(Point p1, Point p2) {
return Math.sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}
}
class NearestPairFinder {
public double findNearestPair(List<Point> points) {
// 按x坐标排序点集
Collections.sort(points, ***paringDouble(p -> p.x));
double minDistance = Double.MAX_VALUE;
// 使用优先队列(最小堆)来维护当前遇到的点中距离上一个点最近的点集
PriorityQueue<Point> minHeap = new PriorityQueue<>(new PointDistanceComparator(points.get(0)));
for (int i = 1; i < points.size(); i++) {
Point current = points.get(i);
// 清除不在当前考虑范围内的点
while (!minHeap.isEmpty() && current.x - minHeap.peek().x > minDistance) {
minHeap.poll();
}
// 将当前点添加到最小堆中
minHeap.add(current);
// 更新最小距离
```
0
0






