误差函数在神经网络中的应用：从理论到实践（权威指南）

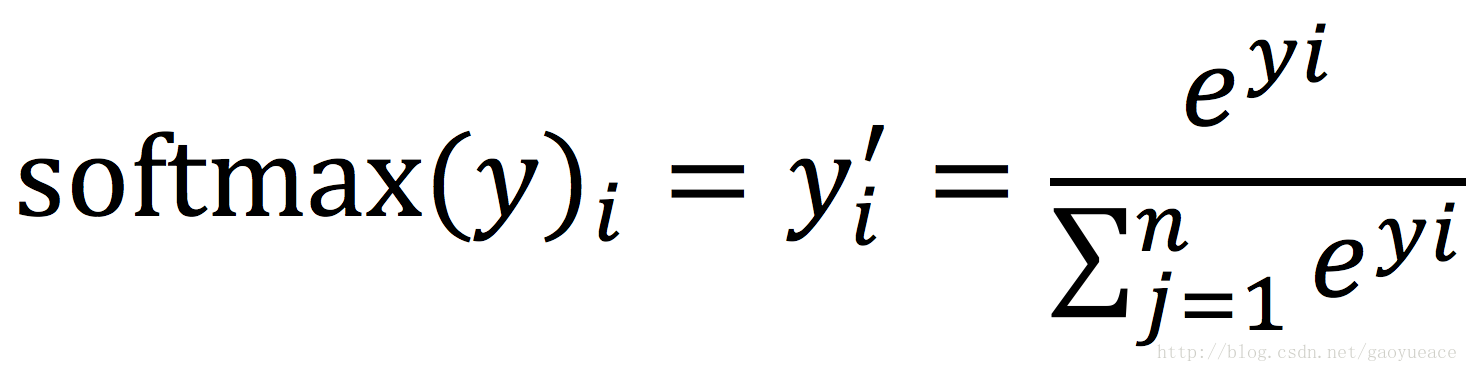
# 1. 误差函数的基础**

### 1.1 误差函数的概念和类型

误差函数，也称为损失函数，是衡量神经网络预测值与真实值之间差异的数学函数。它用于评估模型的性能，并指导模型的训练过程。常见的误差函数类型包括：

- **均方误差 (MSE)**：计算预测值与真实值之间的平方差的平均值。
- **平均绝对误差 (MAE)**：计算预测值与真实值之间的绝对差的平均值。
- **交叉熵误差**：用于分类任务，计算预测概率分布与真实概率分布之间的差异。

# 2. 误差函数在神经网络中的理论

### 2.1 误差函数在神经网络中的作用

误差函数是神经网络中衡量模型预测与真实标签之间差异的函数。它用于指导网络的训练过程，使模型能够学习从输入数据中提取有意义的特征并做出准确的预测。

### 2.2 误差函数的梯度计算

梯度计算是神经网络训练的关键步骤。它用于确定误差函数相对于模型参数的导数。通过反向传播算法，梯度信息可以用于更新模型参数，从而最小化误差函数。

**代码块 1：反向传播算法**

def backpropagation(model, loss_function, inputs, labels):
    """反向传播算法

    Args:
        model: 神经网络模型
        loss_function: 误差函数
        inputs: 输入数据
        labels: 真实标签

    Returns:
        更新后的模型参数
    """

    # 前向传播，计算输出和误差
    outputs = model(inputs)
    loss = loss_function(outputs, labels)

    # 反向传播，计算梯度
    grads = torch.autograd.grad(loss, model.parameters())

    # 更新模型参数
    for param, grad in zip(model.parameters(), grads):
        param.data -= learning_rate * grad

    return model

**逻辑分析：**

代码块 1 展示了反向传播算法，它通过计算误差函数相对于模型参数的梯度来更新模型参数。通过迭代执行此过程，模型可以逐渐学习从输入数据中提取特征并做出准确的预测。

### 2.3 误差函数的优化方法

优化方法用于最小化误差函数，从而找到模型参数的最佳值。常用的优化方法包括：

- **梯度下降法：**一种迭代算法，沿梯度方向更新参数以最小化误差函数。
- **动量法：**一种梯度下降法的变体，它通过引入动量项来加速收敛。
- **RMSProp：**一种自适应学习率优化方法，它通过估计梯度的二阶矩来调整学习率。

**代码块 2：梯度下降法**

def gradient_descent(model, loss_function, inputs, labels, learning_rate):
    """梯度下降法

    Args:
        model: 神经网络模型
        loss_function: 误差函数
        inputs: 输入数据
        labels: 真实标签
        learning_rate: 学习率

    Returns:
        更新后的模型参数
    """

    # 前向传播，计算输出和误差
    outputs = model(inputs)
    loss = loss_function(outputs, labels)

    # 计算梯度
    grads = torch.autograd.grad(loss, model.parameters())

    # 更新模型参数
    for param, grad in zip(model.parameters(), grads):
        param.data -= learning_rate * grad

    return model

**参数说明：**

- `model`：神经网络模型
- `loss_function`：误差函数
- `inputs`：输入数据
-