误差函数在时间序列预测中的应用：揭示数据中的模式（实用指南）

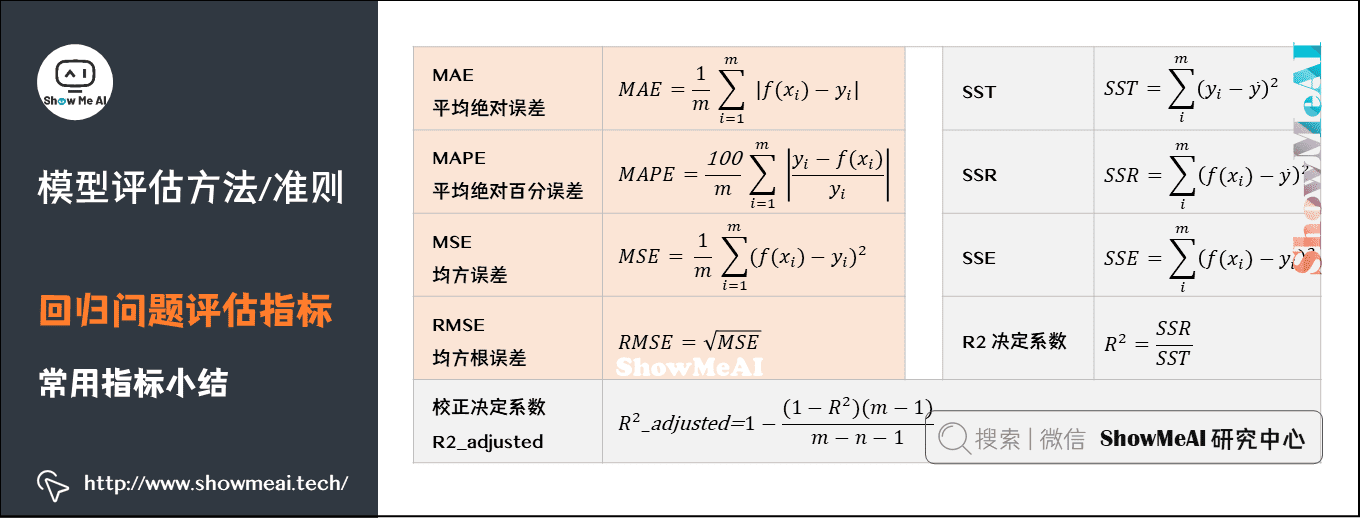
# 1. 误差函数的基本概念和性质

误差函数是衡量模型预测值与真实值之间差异的数学函数。在时间序列预测中，误差函数用于评估预测模型的准确性。

误差函数具有以下性质：

- **非负性：**误差函数的值始终为非负数。
- **对称性：**误差函数关于其均值的左右对称。
- **无偏性：**当模型预测值与真实值相等时，误差函数的期望值为零。

# 2. 误差函数在时间序列预测中的应用理论

### 2.1 时间序列分析的基础知识

时间序列分析是一种统计技术，用于分析和预测随时间变化的数据。时间序列数据通常具有以下特征：

- **相关性：**时间序列数据中的观测值之间通常存在相关性，即当前观测值受过去观测值的影响。
- **趋势：**时间序列数据可能表现出随时间变化的趋势，例如线性趋势或非线性趋势。
- **季节性：**时间序列数据可能存在季节性模式，例如每周或每年的周期性波动。

### 2.2 误差函数在时间序列预测中的作用

误差函数在时间序列预测中扮演着至关重要的角色，它衡量预测值与实际值之间的差异。选择合适的误差函数对于准确预测未来值至关重要。

误差函数的常见类型包括：

- **均方误差 (MSE)：**MSE 是预测值与实际值之间平方差的平均值。MSE 适用于正态分布的数据。
- **平均绝对误差 (MAE)：**MAE 是预测值与实际值之间绝对差的平均值。MAE 适用于非正态分布的数据。
- **对数似然函数 (LLF)：**LLF 是预测值与实际值之间似然函数的对数。LLF 适用于概率模型。

### 2.3 误差函数的选取和评价

误差函数的选取取决于以下因素：

- **数据分布：**误差函数应与数据分布相匹配。例如，对于正态分布的数据，MSE 是一个合适的误差函数。
- **预测模型：**误差函数应与预测模型兼容。例如，LLF 适用于概率模型。
- **预测目标：**误差函数应与预测目标相一致。例如，对于预测准确性，MSE 是一个合适的误差函数。

误差函数的评价可以通过以下指标进行：

- **偏差：**偏差衡量预测值与实际值的系统性差异。
- **方差：**方差衡量预测值的随机性。
- **均方根误差 (RMSE)：**RMSE 是偏差和方差的平方根，它综合考虑了偏差和方差。

通过比较不同误差函数的偏差、方差和 RMSE，可以选择最合适的误差函数。

# 3.1 误差函数在ARMA模型中的应用

#### 3.1.1 ARMA模型的原理和参数估计

ARMA（自回归移动平均）模型是一种经典的时间序列预测模型，它通过自回归项（AR）和移动平均项（MA）来捕捉时间序列数据的自相关性和依赖性。

**自回归项 (AR)**：AR项表示时间序列的当前值与过去的值之间的线性关系。AR(p)模型中包含p个自回归项，表示为：

Y_t = c + ϕ_1 * Y_{t-1} + ϕ_2 * Y_{t-2} + ... + ϕ_p * Y_{t-p} + ε_t

其中：

* Y_t 是时间序列在时间 t 的值
* c 是常数项
* ϕ_1, ϕ_2, ..., ϕ_p 是自回归系数
* ε_t 是白噪声误差项

**移动平均项 (MA)**：MA项表示时间序列的当前值与过去误差项之间的线性关系。MA(q)模型中包含q个移动平均项，表示为：

Y_t = c + ε_